旋转尾翼弹箭极限圆锥运动稳定判据

陈亮， 刘荣忠， 郭锐， 席滔滔， 李培林， 朱桂利， 杨永亮, 邢柏阳, 高科

(1.中国航天科技集团有限公司 第七研究院 第七设计部， 四川 成都 610100; 2.南京理工大学 机械工程学院, 江苏 南京 210094)

0 引言

圆锥运动为弹箭基本的角运动形式之一，是指弹轴绕速度线做圆锥摆动的运动过程。在弹箭气动参数和结构特征参数满足一定条件的情况下，弹箭发射时的初始扰动以及飞行过程中的不确定因素(如阵风等)均可能导致弹箭形成极限圆锥运动。20世纪60年代中期，美国Nitehawk探空火箭在所进行的50余次飞行试验中，出现近20次发散的圆锥运动[1]。西班牙140 mm火箭弹在进行的28次飞行实验中，有9次出现了圆锥运动，导致其飞行速度在1.5 s内降低了60%[2]，这对提高弹箭射程是不利的。

对于以母弹作为扫描探测平台的掠飞灵巧弹药而言，角运动规律对其稳态扫描特性及命中概率有显著影响。当仅受线性空气动力作用时，掠飞灵巧弹药仅需满足线性稳定条件，即可使初始扰动引起的攻角运动幅值随弧长增长而逐渐被衰减为0°[3-4]，从而保证其在弹道末端具有相对稳定的弹体姿态。而当受非线性空气动力作用时，掠飞灵巧弹药在弹道末端可能产生攻角幅值不为0°的极限圆锥运动[5-6]。此时，弹载敏感器在空间和地面形成的扫描线必然随弹轴的锥进运动而出现振荡变化，从而影响目标捕获概率，这是灵巧弹药研制过程中必须加以避免的。因此，研究弹箭在非线性气动力和力矩作用下的角运动规律，确定极限圆锥运动形成条件，对弹箭运动稳定性和命中概率研究具有重要意义。

国内外学者围绕弹箭圆锥运动稳定性问题已取得了丰富的研究成果。Levy等[7]和Clare等[8]基于风洞实验和理论推导证明了马格努斯力和力矩等面外力和力矩是弹箭形成极限圆锥运动的直接原因。李臣明等[9]考虑由章动和进动引起的赤道阻尼力矩系数的差异，基于奇点理论和振幅平面法研究了弹箭在非对称赤道阻尼力矩作用下形成极限圆锥运动的条件，但未考虑非线性静力矩和非线性马格努斯力矩的影响。钟扬威等[10]基于微分方程Hopf分岔理论，研究了当某一参数(如空气密度)改变对极限圆锥运动特性的影响，但该方法难以获得具有明确解析关系的理论模型。邓超[11]基于拟线性法推导了弹箭在非线性静力矩和非线性马格努斯力矩作用下的振幅平面方程，并分析了马格努斯力矩系数线性部分和非线性部分对极限圆锥运动的影响，由于拟线性法需要人为引入附加限制条件，因此限制了其使用范围。此外，文献[5-6]对弹箭非线性角运动特性以及弹箭极限圆锥运动特性的相关研究方法、研究成果进行了全面系统的介绍，其中文献[6]中5.5节基于改进拟线性法推导了旋转弹箭在非线性静力矩和马格努斯力矩作用下的振幅平面方程，给出了形成稳定极限圆锥运动的判据条件以及极限圆锥运动幅值和频率表达式，并结合攻角方程数值计算结果验证了所得判据条件的有效性。但研究发现文献[6]中给出的弹箭极限圆锥运动判定条件在一定条件下并不成立，且相关判据以及极限圆锥运动幅值和频率表达式不够明确(不能根据攻角方程中含有的参数，直接判断极限圆锥运动的稳定性，并计算极限圆锥运动幅值和频率)，这很大程度上限制了相关成果的适用范围。

针对现有理论的不足，本文结合文献[6]的相关研究成果，通过对弹箭在准圆运动状态下的振幅平面方程进行泰勒展开，并分不同情况对方程解的存在性和稳定性进行详细分析。在此基础上，分析了同时在非线性静力矩和非线性马格努斯力矩作用下，弹箭形成稳定极限圆锥运动的必要条件，给出了相应的解析判据，并以某型旋转尾翼弹为例进行算例分析，验证了理论模型的正确性。

1 稳定极限圆锥运动形成条件分析

1.1 非线性攻角方程改进拟线性解

旋转弹箭在非线性静力矩和非线性马格努斯力矩作用下的齐次攻角方程为

Δ″+(H-iP)Δ′-(M+iPT)Δ=0，

(1)

式中：H为俯仰阻尼力矩系数；P为陀螺稳定项，其值主要由弹箭滚转速度及转动惯量决定；M为静力矩系数，M=M0+M2δ2，δ为攻角，M0为静力矩系数线性项，M2为静力矩系数非线性项；T为马格努斯力矩系数，T=T0+T2δ2，其中T0为马格努斯力矩系数线性项，T2为马格努斯力矩系数非线性项。各参数的具体计算式可参见文献[6]。

文献[6]采用改进拟线性代入法对(1)式进行了推导求解，得到了旋转弹箭在非线性静力矩和非线性马格努斯力矩作用下做准圆运动时的振幅平面方程，即

(2)

此时对应的弹箭做准圆运动时的频率为

(3)

(4)

(5)

在实际研究中，已对上述公式推导过程的正确性做了充分的验证，为节约篇幅，本文不再对上述表达式的推导过程作详细介绍，而是在其基础上，对旋转弹箭形成稳定极限圆锥运动的判据作进一步分析。

1.2 非零奇点存在性条件

(6)

于是，弹箭准圆运动振幅平面方程(2)式的第1式可表示为

(7)

(8)

(9)

当PT2≠0时(包括PT2<0、PT2>0两种情况)，由(9)式可得

(10)

(11)

进一步对(9)式进行整理得

(12)

当M2≠0时，有m2=M2/0≠0，将代入(12)式可得

(13)

令A=PT2/(H0m2)、B=P(2T0-H0)/(2H0)，则(13)式可简化为

(14)

对(14)式左右平方，并进行整理，可得

(15)

当弹箭形成稳定极限圆锥运动时，要求(15)式具有实数解，即必须有

(2AB+0)2-4A2(B2+0)>0，

(16)

0(4AB-4A2+0)>0.

(17)

将A和B表达式代入(17)式，可得

(18)

当满足(11)式、(18)式时，可得(8)式的解为

mc=mc1或mc=mc2，

(19)

式中：

1.3 非零奇点的稳定性条件

(20)

(21)

(22)

(23)

由此解得

(24)

(25)

(25)式成立的条件为

(26)

(27)

2 稳定极限圆锥运动形成判据

旋转弹箭形成稳定极限圆锥运动需要同时满足奇点存在性和稳定性两方面的条件，当PT2≠0且M2≠0时，即需同时满足(11)式、(18)式、(24)式以及(27)式。下面通过进一步分析，给出PT2和M2的不同取值情况下，旋转弹箭稳定极限圆锥运动判据。

2.1 PT2<0且M2≠0情况

由(11)式中的第1式和(27)式可得

(28)

由(28)式可知，当H0≤0时，此不等式时不成立，因此必须有H0>0，于是(28)式可进一步解得

(29)

由(29)式可知，当PT2<0，必有H0>0是形成稳定极限圆锥运动的必要条件。

对(24)式进行整理得

(30)

将(30)式与(29)式联立，可得

(31)

由(31)式可解得

(32)

综上所述，当PT2<0时，弹箭在非线性马格努斯力矩和非线性静力矩作用下形成稳定极限圆锥运动的条件可表示为

(33)

式中：J1、J2、J3、J4、J5为便于分析所定义的5个判定参数，

此时有对应的极限圆锥运动幅值和频率为

(34)

(34)式中mc即为由(19)式解出，且同时满足(33)式所有判据条件的解。

2.2 PT2>0且M2≠0情况

由(11)式中的第2式可得

(35)

此时无法直接确定H0的符号，考虑到通常弹箭具有正阻尼，因此这里只考虑H0>0的情况。在此条件下，必有

(36)

由(24)式可得

(37)

由(37)式可以看出，当H0>0时，为使(37)式成立必须有M2<0，即T2和M2不能同时大于0，这是因为二者同时大于0时，静力矩和马格努斯力矩非线性项均是促使攻角幅值增大的，此时无法形成稳定的极限圆锥运动。由(37)式还可以解得

(38)

由(35)式与(38)式联立可得

(39)

为使(39)式成立，必有

(40)

由此可解得

(41)

综上所述，结合(18)式、(24)式、(35)式及(41)式可得，当H0>0且PT2>0时，弹箭在非线性马格努斯力矩和非线性静力矩作用下形成稳定极限圆锥运动的条件可简化为

(42)

式中：Q1、Q2、Q3、Q4为判定参数，

此时，对应的极限圆锥运动幅值和频率为

(43)

式中：mc即为由(19)式解出，且同时满足(42)式所有判据条件的解。

2.3 PT2=0且M2≠0情况

由(11)式中的第3式可得

(44)

(45)

(46)

(44)式代入(46)式可得

(47)

进一步对(44)式进行求解，可得

(48)

(49)

(48)式代入(3)式可得由3次方静力矩引起的极限圆锥运动频率为

(50)

由(50)式可知，当仅考虑静力矩非线性时，极限圆锥运动频率表达式可化为极为简单的形式。

综上所述，旋转弹在3次方非线性静力矩作用下，形成稳定极限圆锥运动的条件为

(51)

由(51)式可知，正阻尼(H0>0)以及负的3次方静力矩系数(M2<0)是形成稳定极限圆锥运动的必要条件。

2.4 M2=0情况

当仅考虑马格努斯力矩非线性时(M2=0，T2≠0)，这种情况相对简单，为节约篇幅这里不做详细推导。采用与2.3节相似推导过程可得，此时存在稳定极限圆锥运动的条件为

(52)

相应地，可得到形式较为简单的极限圆锥运动幅值和频率表达式：

(53)

2.5 综合判据

由(33)式和(42)式可知，无论PT2<0或PT2>0时，为形成稳定极限圆锥运动都需要满足两条完全相同的判据条件，即

(54)

对于PT2=0的情况，将T2=0代入(54)式，可得

(55)

由(55)式可知，当PT2=0时，J1>0恒成立，由J2>0可解得M2<0，这与(51)式给出的判据是一致的。因此，对于PT2<0、PT2>0以及PT2=0的情况，(54)式均是形成稳定极限圆锥运动的必要条件，故定义(54)式为综合判据。

由(54)式可知，判据J2为关于T2和M2的线性函数，J1可视为关于(T2/M2)的2次函数，且当0<0时，J1关于(T2/M2)的函数图像是开口向上的2次曲线，当0>0时，J1关于υ=T2/M2的函数图像是开口向下的2次曲线，利用相关性质可对弹箭极限圆锥状态进行判断。

3 算例分析

为检验所得理论判据的有效性，以某型旋转尾翼弹气动及结构特征参数作为基本参数，以3次方马格努斯力矩系数T2作为分析变量，对旋转弹箭极限圆锥运动特性进行算例分析，基本参数如表1所示。

表1 基本参数

由2.4节可知，无论T2取何值(M2≠0时)，弹箭形成极限圆锥运动时，均需满足综合判据(54)式。为直观分析判据J1和J2随T2对的变化规律，首先，按表1对其余气动参数进行取值，并由(54)式作出J1和J2关于T2的变化曲线，以确定使判据J1>0和J2>0同时成立时，T2所需满足的取值范围。在此基础上，计算T2在不同取值下其余判据的取值，并预测极限圆锥运动形成情况。最后，将所选取参数组合代入攻角方程，并采用龙格库塔法进行直接求解，以检验理论模型的正确性。

考虑到当M2和0取不同值时，判据J1>0和J2>0解的性质具有一定差异，因此对3种情况进行分析。

3.1 M2<0与0<0情况

图1给出了按表1参数进行取值时，判据J1和J2随T2的变化曲线，此时，有M2=-0.35<0，P(2T0-H0)=0.038>0，0=M0-P2/4=-0.019 5<0. 由图1可知，当T2<1.152或T2>1.562时，判据J1>0成立，当T2<1.326时，判据J2>0成立，为保证J1>0、J2>0同时成立，须有T2<1.152，这是形成稳定极限圆锥运动的必要条件。

图1 判据J1和J2曲线(M2<0，0<0)Fig.1 Curves of criteria J1 and J2 for M2<0 and 0<0

其余参数保持不变，T2分别取-2.00、-1.00、0、1.15、1.16、1.60. 一方面，根据T2的不同取值，分别由(33)式、(42)式及(51)式计算各判据条件，结果如表2所示。表2中当T2≠0且J1>0时，mc存在两个可能的取值，即mc1和mc2，其值由(19)式给出。分别将mc=mc1和mc=mc2代入(33)式和(42)式，可得J3、J4及J5(或Q3、Q4及Q5)，进而判断mc1和mc2中是否存在完全满足所有判定条件的解。若存在，则将相应的mc值代入(34)式和(43)式中，得到由理论预测的极限圆幅值Kc和频率φ′c. 表2中状态项T表示形成了极限圆锥运动，F表示未形成极限圆锥运动。另一方面，将表1和表2给出参数代入攻角方程，并采用龙格库塔法对攻角方程进行迭代求解，得到T2取不同值时的攻角曲线，结果如图2所示。

对比表2和图2可知，在不同T2取值下，数值计算结果与表2预测结果完全一致，即当T2<1.152时，弹箭形成了稳定极限圆锥运动，而当T2>1.152时，弹箭攻角发散，未形成稳定极限圆锥运动，其中，T2=1.15的攻角曲线变化规律已达到临界状态(即将发散)，而当T2=1.16时，攻角曲线已出现发散，表明本文给出的稳定极限圆锥运动判据具有很高的灵敏度。由表2的结果可知，当T2=1.60时判据J1>0，存在两个可能的奇点位置，分别对应mc=mc1和mc=mc2，但这两个奇点位置均不能使其余判据完全成立，故不能形成稳定极限圆锥运动。由此说明，判据J1>0是保证攻角方程奇点存在性的必要条件，而其余判据则是保证奇点为稳定结点的必要条件，在对弹箭极限圆锥运动状态进行预测时，必须对所有判据进行检验。此外，对比算例T2=-1.00、T2=0、T2=1.15的结果可知，极限圆锥运动幅值和频率均随3次方马格努斯力矩系数T2增加而增大。

表2 极限圆锥运动验证算例(M2<0，0<0)

Tab.2 Example for verification of limiting conical motion (M2<0，0<0)

表2 极限圆锥运动验证算例(M2<0，0<0)

T2J1J2其他判定条件状态mcδcφc-1.001.8×10-38.8×10-3mc1=12.6、J3=-0.42、J4=1.8、J5=0.14Fmc2=1.33×10-2、J3=8.0×10-4、J4=0.32、J5=0.23T1.33×10-21.740.20706.0×10-45.0×10-3^M0+[P(2T0-H0)]2/4H20=5.5×10-3T2.330.2081.153.6×10-77.0×10-3mc1=0.428、Q3=2.8×10-2、Q4=-2.7×10-3Fmc2=0.296、Q3=2.0×10-2、Q4=2.9×10-3T0.2968.240.2281.16-9.9×10-76.0×10-4F1.605.7×10-6-1.0×10-3mc1=-0.153、Q3=-1.4×10-2、Q4=-1.4×10-2Fmc2=-0.427、Q3=-4.0×10-2、Q4=1.7×10-3F

图2 不同T2下的攻角曲线(M2<0，0<0)Fig.2 Angle-of-attack curves with different T2 for M2<0 and 0<0

3.2 M2<0与0>0情况

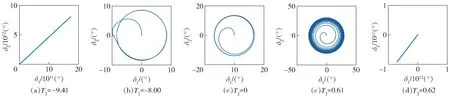
图3给出了当M0=0.01，其余参数按表1取值时，判据J1和J2随T2的变化曲线，此时M2=-0.35<0，0=M0-P2/4=0.007 5>0，且有P(2T0-H0)=0.038>0. 由图3可知，当-9.4880成立，当T2<1.326时判据J2>0成立，为保证J1>0、J2>0同时成立，须有-9.488

图3 判据J1和J2曲线(M2<0，0>0)Fig.3 Curves of criteria J1 and J2 for M2<0 and 0>0

其余参数保持不变，T2分别取-9.49、-9.48、-9.41、-8.00、-1.00、0、0.61、0.62，按(33)式、(42)式及(51)式进行分析计算，结果如表3所示。按表1和表3给出参数代入攻角方程，并采用龙格- 库塔法对攻角方程进行迭代求解，得到T2取不同值时的攻角曲线，部分结果如图4所示。

表3 极限圆锥运动验证算例(M2<0，0>0)

Tab.3 Example for verification of limiting conical motion for M2<0 and 0>0

表3 极限圆锥运动验证算例(M2<0，0>0)

T2J1J2其他判定条件状态mcδcφc-9.49-3.4×10-74.1×10-2F-9.486.3×10-74.1×10-2mc1= -1.05、J3=0.14、J4=-2.8×10-2、J5=2.0Fmc2= -1.08、J3=0.13、J4= -1.6×10-2、J5=1.8F-9.417.3×10-64.1×10-2mc1= -1.03、J3=0.14、J4=-4.1×10-2、J5=2.4Fmc2= -1.12、J3=0.13、J4= -9.0×10-4、J5=1.6F-8.001.2×10-43.5×10-2mc1= -1.02、J3=0.14、J4=-4.5×10-2、J5=2.5Fmc2= -1.56、J3=9.3×10-2、J4= 9.8×10-2、J5=1.1T-1.5610.490.115-1.001.3×10-48.8×10-3mc1= -2.64、J3=4.7×10-2、J4=0.24、J5=0.29Tmc2= -38.6、J3=-0.37、J4= 1.6、J5=0.14F-2.6413.640.16105.6×10-55.0×10-3^M0+[P(2T0-H0)]2/4H20=3.3×10-2T-4.3417.480.2080.619.5×10-72.7×10-3mc1=-12.96、Q3=0.14、Q4=9.1×10-3Tmc2=-21.17、Q3=0.23、Q4=-7.0×10-3F-12.9630.200.3500.62-1.6×10-82.7×10-3F

图4 不同T2下的攻角曲线(M2<0，0>0)Fig.4 Angle-of-attack curves with different T2 for M2<0 and 0>0

3.3 M2>0与0>0情况

图5为当取M0=0.01、M2=0.35>0，其余参数按表1进行取值时，判据J1和J2随T2的变化曲线，此时0=M0-P2/4=0.007 5>0，且有P(2T0-H0)=0.038>0. 由图5可知，无论T2取何值，均不能使判据J1>0、J2>0同时成立，即在此条件下，无法形成稳定极限圆锥运动。其余参数保持不变，T2分别取-1.0、-0.5、0、1.0对攻角方程进行求解计算，结果表明(见图6)，数值计算结果与理论分析结果是一致的，即在本文选取的参数条件下，当M2>0、0>0时，T2无论取何值均无法形成稳定极限圆锥运动。

图5 判据J1和J2曲线(M2>0，0>0)Fig.5 Curves of criteria J1 and J2 for M2>0 and 0>0

图6 不同T2下的攻角曲线(M2>0，0>0)Fig.6 Angle-of-attack curves with different T2 for M2>0 and 0>0

4 结论

本文通过对弹箭在准圆运动状态下的攻角运动振幅平面方程，进行泰勒展开处理，进而对其非零奇点的存在性和收敛性进行了分类讨论，得到了不同参数条件下，弹箭形成稳定极限圆锥运动的判据条件，及其极限圆锥运动幅值和频率表达式，并以某型旋转尾翼弹参数为例对相关结果进行了验证。通过上述研究，得出以下结论：

1)本文给出的判据条件与现有研究相比具有更明确的解析关系，且所考虑的参数范围更为全面。算例分析结果表明，本文推导得到的旋转弹箭在非线性马格努斯力矩和非线性静力矩作用下形成极限圆锥运动的判据条件，能准确预测弹箭极限圆锥运动形成情况，验证了理论模型的正确性。

2)当M2≠0时，对于PT2<0、PT2>0以及PT2=0的情况，弹箭形成稳定极限圆锥运动均需满足本文给出的仅与攻角方程初始参数有关的两条综合判据条件J1>0和J2>0. 虽然判据J1>0和J2>0仅是形成稳定极限圆锥运动的必要条件，但算例分析结果显示，当攻角方程各参数满足这两条判据时，在大多数情况下弹箭均会形成稳定极限圆锥运动，根据这两条判据可方便快捷地对弹箭的极限圆锥运动特性进行初步判断。

3)对于本文分析的4种参数取值情况均有仅当T2和M2中至少一个为负值时，才可能形成稳定极限圆锥运动，这是因为正的T2和M2均是促使角运动发散的因素，当二者均为正时弹箭准圆运动无法收敛。此外，对于PT2<0且M2≠0、PT2=0且M2≠0、M2=0 3种情况均可由理论推导严格证明具有正阻尼H0>0是旋转弹箭形成稳定极限圆锥运动的必要条件，而对于PT2>0且M2≠0这一情况无法严格证明这一结论，因此本文结合掠飞灵巧弹药气动特性，在假设H0>0的条件下，推导了稳定极限圆锥运动形成判据。