关于Michalik连分式插值的多点扩展应用

孙思梦

（安徽理工大学数学与大数据学院，安徽淮南232001）

自然科学与工程技术中，经常会遇到一些复杂函数或复杂的散乱数据的整理。而有理函数就为其提供了很好的解决办法。连分式插值函数有着广泛的研究与应用,早期，王仁宏，谭结庆等对连分式插值的各种计算方法做了总结[1-3]，其基本概念和插值方法已经深有研究[4-9]，许多学者对有理样条函数[10]以及一系列混合有理函数[11-14]做了讨论。文献[15]给出了新的用组合术语重新表述了几个关于连分式的已知结果，这些多边形剖分被解释为Farey 镶嵌中的行走。连分式的组合模型可以进一步发展，以获得问题陈述语言系统(problem statement language，PSL)。近些年，随着科学技术的发展，连分式有理插值有了更广泛的应用[16-20]。文献[21]定义和研究了卷积交流幂和，并证明了一些涉及欧拉多项式和斯特林数的恒等式，导出了转换器分子和分母的显式公式。特别地，当t是一个偶数正整数时，得到了调和连分式的极限值。这些都是关于连分式更进一步的研究应用。本文对Michalik 连分式做了研究，给出了一种对Michalik 连分式插值的扩展算法，与一般的连分式算法进行了比较，说明了该扩展的插值方法的有效性。该方法也可用于实际生活中含有渐近线的散乱数据来构造插值函数，则可以算出最优节点的情况。

1 连分式插值

连分式插值是一种有理函数逼近法。其基本出发点是将原型展开成连分式然后截取前几个起主要作用的偏系数构成简化模型。它是由初期的数量形式推广到向量形式和矩阵形式的研究内容。随着科学技术的发展，连分式的应用范围也在不断扩大，特别是以连分式为工具的数值逼近方法尤其受到人们的重视。连分式计算简便，拟合精度较高，是一种很有效的传递函数简化法。

设给出的点集X={x0,x1,…,xn}⊂[a,b]，函数f(x)在其上有定义，则X上的Thiele 型连分式插值为：

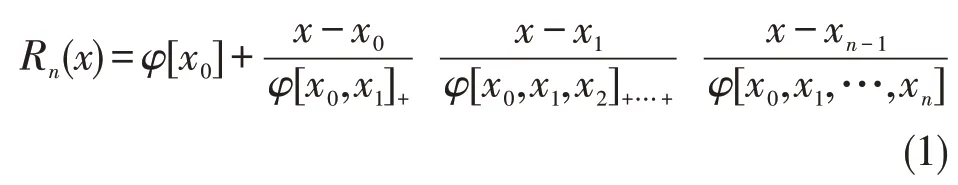
其中φ[x0,x1,…,xk]是f(x)在x0,x1,…,xk处的k阶逆差商，其定义如下：

上述有理插值函数Rn(x)是分子次数为且分母次数为的有理函数，即对于已知的型值点(xi,yi)(yi=f(xi),i=0,1,2)，连分式插值函数为：

2 三项递推公式

设x0，x1，…，xn为区间[a，b]上的n+1 个不同的插值节点，fi=f(xi)，i=0，1，…，n是被插值函数f(x)在这些节点处对应的函数值，设插值连分式为，给出pn和Qn的递推关系[1]：

设P-1=1，P0=a0,Q-1=0,Q0=1则对n≥1，

利用三项递推公式可以逆向推导出所加节点的函数值，从而使该函数更加精准。

3 关于Michalik 连分式插值的扩展算法

Michalik 在1983 年为了寻找在物理学中的一些非线性方程组的数值算法，从而创造性地建立了系数函数的递推格式，首次提出Michalik 连分式插值算法。即在一些有极限的情况之下，当它们所有节点都等同的时候，插值函数就转换成了在这些插值节点附近的连分式的展开。

对于任意非零的实值函数f(x)及其对应的函数表x0，x1，…，xn，f(x0)，f(x1)，…，f(xn)，首先将该函数描述成以下形式：

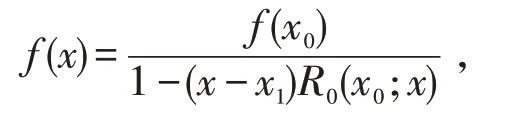
将函数表中的第一个点代入，得到

若上述函数的乘积存在，则下述极限存在：

则插值连分式误差计算公式

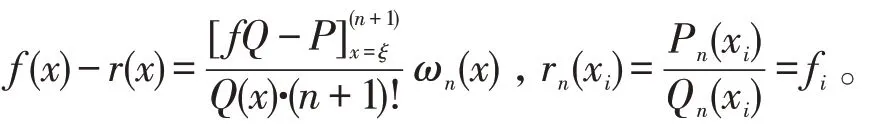
插值连分式的特征定理为：

设点集X={x0,x1,,xn},n=2m-1，且函数有水平渐进线，即，则Michalik 连分式插值函数为:

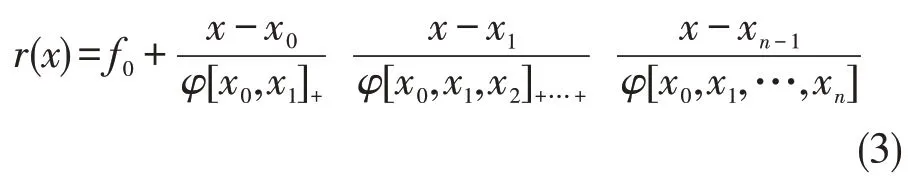
加一点xn+1，已知，则设定的扩展连分式插值函数的极限也为A，根据则能够求出φ[x0,x1,…,xn+1]的值。利用连分式插值的三项递推公式求解出f(xn+1)的值，则可以确定构造出的新的插值节点和连分式插值函数。然后给出不同的插值节点进行比较，得出最优的插值节点及插值函数。

4 数值例子

根据上述理论研究，给出如下的数值例子，从而验证该方法的有效性和实用性。

该函数图像如图1。根据该被插值函数图像，我们可以看出当x趋于无穷大时，f(x)有极限为1。利用一般公式计算出连分式插值为：

可以计算出其误差函数图像如图2 所示。关于Michalik 连分式插值的扩展算法如下：

加一个点(x4,f4)，x4=9，计算扩展连分式插值，则可以列出公式：

由公式可以求出φ[x0,…,x4]=0.007 640 9，然后根据三项递推公式计算出f(xn+1)的值。从而计算出的扩展Michalik 连分式插值函数为：

图1 f(x)=的图像

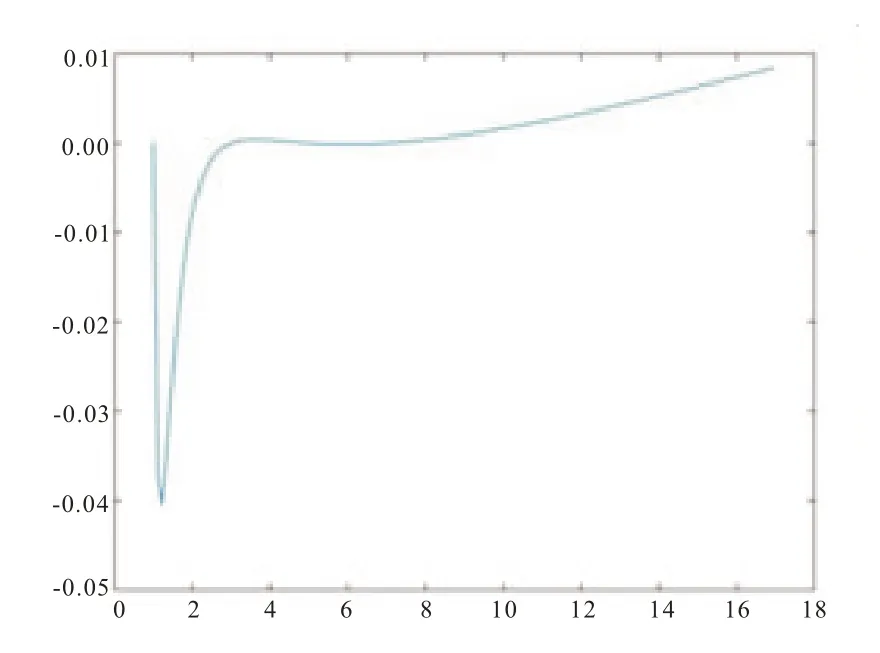
图2 一般连分式插值函数误差图

其误差函数图像如图3 所示。

由两种连分式方法所得出的误差函数图像可以明显看出：随着自变量的增加，一般连分式方法误差逐渐增加，而本文中的扩展Michalik 连分式算法所计算出的函数随着x的增加，误差反而逐渐变小，这就表明了该扩展方法的有效性。

下面对两种连分式插值函数做积分，积分区间为x∈[1.1,10.9]:

图3 扩展Michalik 连分式插值函数误差图像

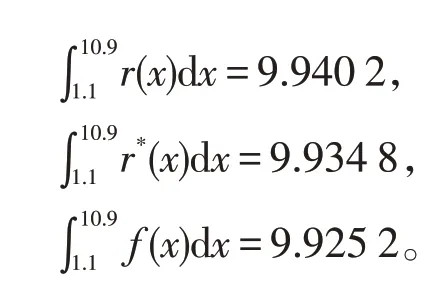
显然，上述例子的比较验证了一个结论：加一个插值节点的扩展Michalik 连分式插值方法得出的函数误差会较小，使给出的连分式插值更加准确，因此该方法更加有效，具有可行性。

5 小结

本文首先将原有的插值节点进行一般的连分式插值算法，然后通过加一个插值节点，进行扩展Michalik 连分式算法，并将偶数个节点化为奇数个节点，使连分式插值的分子次数比分母次数高一次。然后通过添加不同的插值节点，给出不同的节点值，比较验证得出更加精确的扩展的插值函数。通过确定其增加的插值节点，使给出的Michalik 连分式更加趋近于原来给出的函数。这种方法使扩展的连分式插值误差比原来更小，连分式插值算法更加准确，提高了精确度。这是一种可行的有效插值方法，对插值计算和误差估计有重要的影响和推动作用。