一类Caputo分数阶脉冲微分方程Cauchy问题解的存在性
李耀红,张海燕
(宿州学院数学与统计学院,安徽宿州234000)
分数阶微分方程模型由于能更精确的描述一些复杂的自然科学现象,其理论研究在多个学科中有广泛应用,如化学、生物学、材料学、医学、控制理论、信号和图像处理等[1-5]。脉冲微分方程一般用于描述具有不连续跳跃或者突变的物理过程模型。近年来,随着分数阶微分应用理论研究的深入,分数阶脉冲微分方程引起国内外学者的广泛关注,并获得了一些优秀的研究成果[6-13]。特别地,在文[6]中一类Caputpo 分数阶脉冲微分方程Cauchy 问题
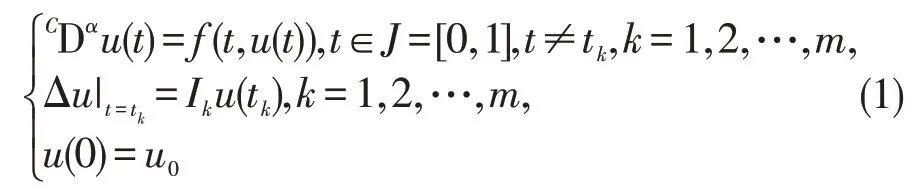
1 预备知识
为方便叙述,引入如下符号和常用定义:

定义1[2]函数g:(0,+∞)→R 的α>0 阶Riemann-Liouville 分数阶积分定义为
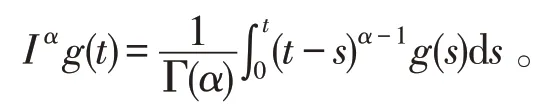
定义2[2]连续函数g:(0,+∞)→R 的α>0 阶Caputo 分数阶导数定义为
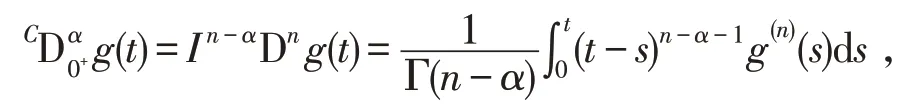
其中当α为非正整数时,n=[α]+1,[α]表示α的整数部分;当α为正整数时时,n=α。
引理 1[2]若函数g∈Cn(0,1)⋂L1[0,1]且α>0,则分数阶微分方程有解
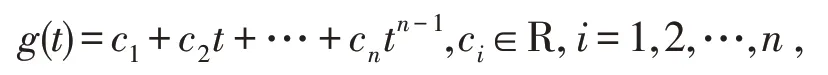
其中n如定义2所述。
引理2[2]若函数g∈L1([0,1],R)且p>q>0 ,则对任意t∈[0,1],有
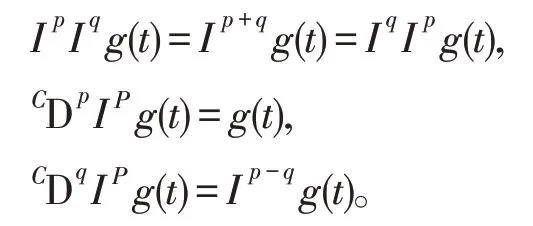
令L1([0,1],R+)表示在范数下从[0,1]到R的可积函数的Banach空间。
引理3[15]若q>0,f∈L1([0,1],R+),则有
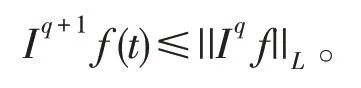
引理4[19](Leray-Schauder 不动点定理)设E是实Banach 空间,D是E中有界凸闭集,T:D→D是一个全连续算子,则T在D中必具有不动点。
引理5[14]若函数u∈L1(0,1)是分数阶脉冲微分方程Cauchy 问题(1)的解当且仅当u∈L1(0,1)是如下积分方程的解:
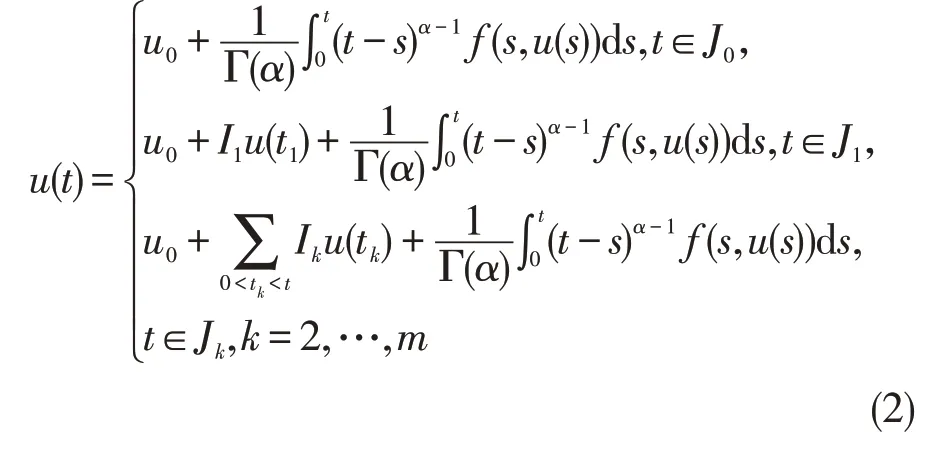
2 主要结果
为叙述方便,给出如下关于函数f的若干非线性增长条件:
(H1)存在非负函数a1i(t)∈L1([0,1],R+),i=1,2 和非负常数lk,k=1,2,…,m,使得对∀t∈[0,1]和u∈R,有
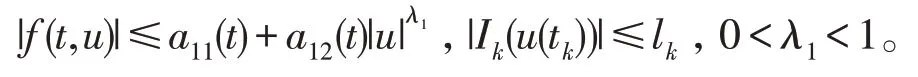
(H2)存在非负函数a2i(t)∈L1([0,1],R+),i=1,2 和非负常数lk,k=1,2,…,m,使得对∀t∈[0,1]和u∈R,有
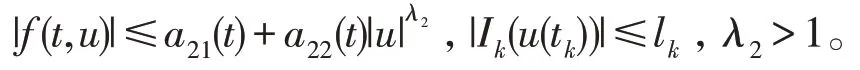
(H3)存在非负函数a3i(t)∈L1([0,1],R+),i=1,2 和非负常数lk,k=1,2,…,m,使得对∀t∈[0,1]和u∈R,有
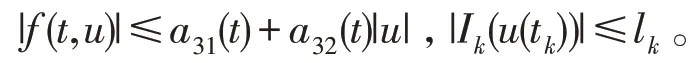
为简便,记
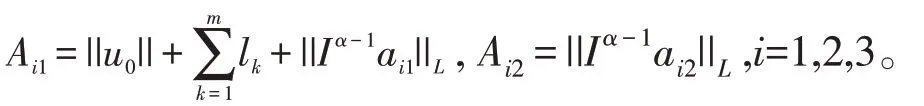
定理1如果条件(H1)满足,则分数阶脉冲微分方程(1)在PC[J,E]中至少存在一个解。
证明定义算子F:PC[J,E]→PC[J,E],令
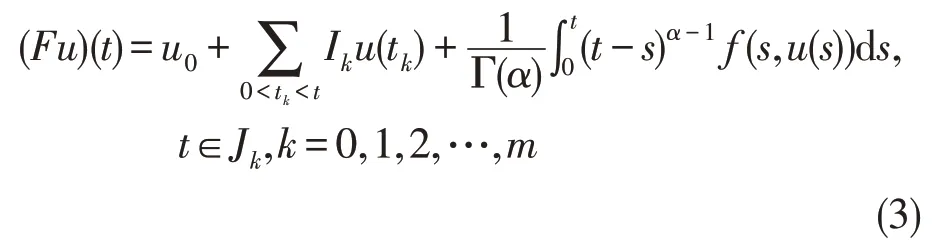
由引理5 知,分数阶脉冲微分方程(1)在PC[J,E]中至少存在一个解,当且仅当算子F在PC[J,E]中至少存在一个不动点。首先令
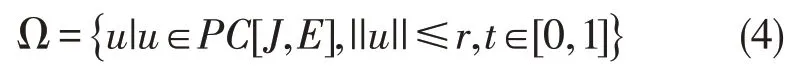
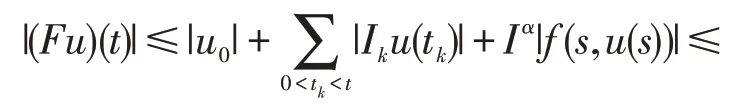
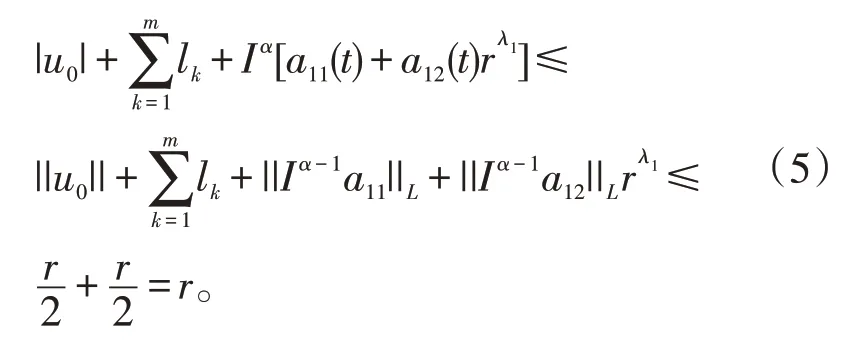
因此算子FΩ ⊆Ω。同时注意到f是连续函数,类似于文献[14],可证得F在Ω 中连续。记
下面证明F在Ω 中是全连续的。对∀u∈Ω,t,τ∈Jk=(tk,tk+1],τ 显然,当τ→t时,|(Fu)(t)-(Fu)(τ)|→0,即FΩ是等度连续的,又注意到FΩ ⊆Ω,知算子F在Ω中是一致有界的。因此由Azela-Ascoli 定理知算子F在Ω 中是全连续的。从而由引理4 知算子F在PC[J,E]中至少存在一个不动点。 定理2如果条件(H2)和满足,则分数阶脉冲微分方程(1)在PC[J,E]中至少存在一个解。 证明与定理1 相似,将式(4)中r满足条件修改为即可。 定理3如果条件(H3)和A32<1 满足,则分数阶脉冲微分方程(1)在PC[J,E]中至少存在一个解。 证明与定理1 相似,将式(5)中r满足条件修改为即可。 例1考虑下列分数阶脉冲微分方程 这里α=0.5,0<λ<1,a11(t),a12(t)为非负可积函数,故由定理1可知分数阶脉冲微分方程至少有一解。 本文利用Leary-Schauder 不动点定理,结合一些非线性增长条件和分数阶积分不等式,获得了一类分数阶脉冲微分方程Cauchy 问题解的存在性。改进了已有文献仅考虑线性增长条件的结果,如[8,14]。同时也注意到,若问题(1)中的分数阶为高阶或非线性项函数中含有分数阶导数,本问题将更具一般性,应用范围也将更广泛。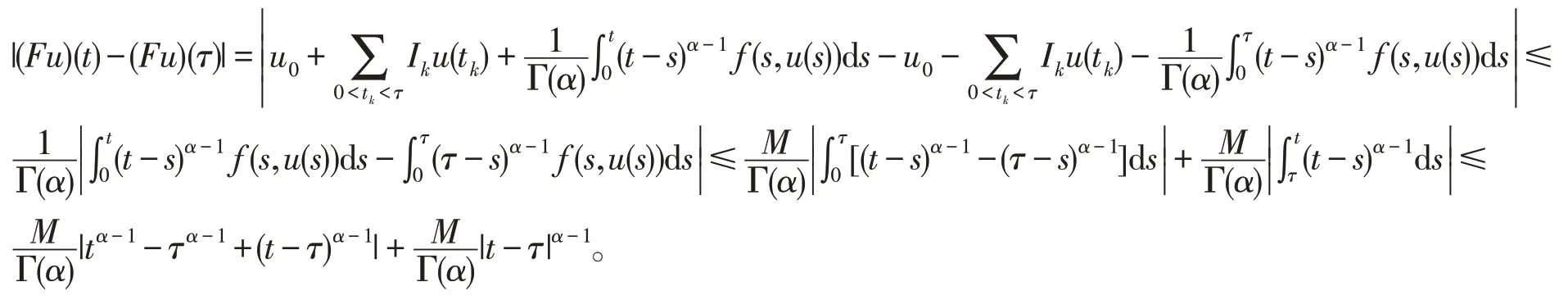
3 例题
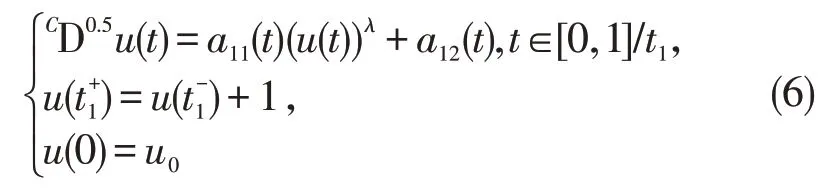
4 小结

