借助伸缩变换 化圆解椭圆

广东省广州市第十六中学(510080) 温伙其

设点P(x,y) 是平面上的任一点，在变换φ:的作用下，点P(x,y) 对应到点P′(x′,y′)，则称φ为平面直角坐标系中的伸缩变换.在此变换下，有以下常用性质:

性质1在φ的作用下，点仍然对应点，直线仍然对应直线，若一个点在直线上，变换后的对应点也在对应直线上.

性质2在φ的作用下，两条平行直线的像仍然平行，两条相交直线像仍然相交，共点的直线的仍然是共点直线.

性质3在φ的作用下，A,B两点分别对应到A′,B′两点，若直线AB的斜率为k，直线A′B′的斜率为k′，则

性质4在φ的作用下，线段AB对应到线段A′B′，设它们的长度分别为|AB|,|A′B′|，则

性质5在φ的作用下，不共线的三点A,B,C分别对应到不共线的三点A′,B′,C′，设ΔABC的面积为S，ΔA′B′C′的面积为S′，则

特别的，在φ的作用下，椭圆=1(a ＞b ＞0)变换为单位圆x′2+y′2=1.

根据上述伸缩变换的特殊性质，我们可把椭圆变换为圆，则直线与椭圆的位置关系转化为直线与圆的位置关系.而圆是我们相当熟悉的几何图形，具有较多特殊性质.在圆中研究图形的特征和位置关系后再还原到椭圆中，从而得到椭圆的相应特征和位置关系，以此开辟研究椭圆问题的另一途径，也可达到简化计算的功能.下面通过高考真题阐述以上伸缩变换性质的应用.

一、求斜率的应用

例1(2015年高考新课标Ⅱ卷理科第20 题(节选))已知椭圆C:9x2+y2=m2(m ＞0)，直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M.

(Ⅱ)若l过点(,m)，延长线段OM与C交于点P，四边形OAPB能否为平行四边形? 若能，求此时l的斜率;若不能，说明理由.

解析令椭圆变换为单位圆x′2+y′2=1，点(,m) 变换为点(1,1)，如下图1.1∼1.2，要使四边形OAPB为平行四边形，根据伸缩变换的图形不变性知，四边形O′A′P′B′应为菱形，则O′到直线A′B′的距离为设直线A′B′的斜率为k′，且知直线A′B′过点(1,1)，故直线A′B′的方程为y′-1=k(x′-1)，即kx′-y′-k′+1=0，则由伸缩变换性质3 知所以k=3k′，因此解得直线l的斜率

图1.1

图1.2

感悟原椭圆的平行四边形在伸缩变换后变为菱形，点(,m)在伸缩变换后变为点(1,1)，因此圆心O′到直线A′B′的距离就等于容易求得直线A′B′的斜率为k′，进而求得原直线l的斜率.所以涉及椭圆弦斜率的处理，我们都可类似解决.

二、求弦长的应用

例2(2016年高考四川卷理科第20 题) 已知椭圆=1(a ＞b ＞0) 的两个焦点与短轴的一个端点是直角三角形的3 个顶点，直线l:y=-x+3 与椭圆E有且只有一个公共点T.

(Ⅰ) 求椭圆的方程及点T的坐标;

(Ⅱ) 设O是坐标原点，直线l′平行于OT，与椭圆E交于不同的两点A、B，且与直线l交于点P.证明: 存在常数λ，使得|PT|2=λ|PA|·|PB|，并求λ的值.

图2.1

图2.2

解析(Ⅰ)易得椭圆E的方程为;点T的坐标为(2,1);

②×③得:

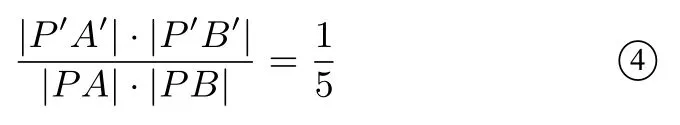
①÷④得:

再根据相交弦定理，有|P′T′|2=|P′A′|·|P′B′|，代入⑤得所以存在常数使得|PT|2=

感悟椭圆的弦长公式而圆的弦长公式两者对比，圆的弦长垂径定理几何处理天然优胜于椭圆的弦长的代数处理.所以涉及椭圆的弦长计算，不妨借助伸缩变换，先转换为求单位圆的弦长，然后再还原为椭圆弦长.

三、求椭圆内接三角形的面积及其最值的应用

例3(2011年高考山东卷理科第22 题(节选))已知直线l与椭圆交于P(x1,y1)，Q(x2,y2)两不同点，且ΔOPQ的面积SΔOPQ=其中O为坐标原点.(Ⅲ) 椭圆C上是否存在点D，E，G，使得SΔODE=SΔODG=SΔOEG=若存在，判断ΔDEG的形状;若不存在，请说明理由.

解析令变换为单位圆x′2+y′2=1，椭圆上的点D，E，G，变换为单位圆上的点D′，E′，G′，由伸缩变换性质5 知同理根据正弦定理面积公式，有

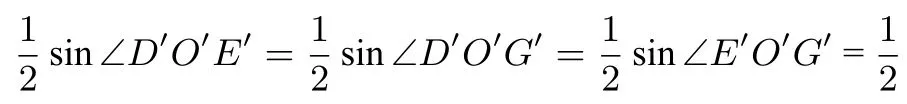
解 得∠D′O′E′=∠D′O′G′=∠E′O′G′=因 为∠D′O′E′+∠D′O′G′+∠E′O′G′=/=2π，所以单位圆上不存在三点D′，E′，G′，使得SΔO′D′E′=SΔO′D′G′=因此椭圆C上不存在点D，E，G，使得SΔODE=SΔODG=SΔOEG=

感悟椭圆的内接三角形面积问题一般都是弦长结合点线距离求解，而伸缩变换到单位圆后，三角形面积可以正弦定理转化为角解决，也可用圆的垂径定理求得底和高解决，极大的拓展了解题方向.

四、求椭圆内接四边形的面积及其最值的应用

例4(2008年高考全国Ⅱ卷理科第21 题(节选))设椭圆中心在坐标原点，A(2,0)，B(0,1)是它的两个顶点，直线y=kx(k ＞0)与AB相交于点D，与椭圆相交于E、F两点.(Ⅱ)求四边形AEBF面积的最大值.

解析依题意得椭圆的方程为直线AB的方程为x+2y=2.在伸缩变换下，椭圆变换为单位圆x′2+y′2=1，且点A′,B′的坐标分别为(1,0),(0,1)，如下图3.1∼3.2，由圆的图形性质知，当A′B′⊥E′F′时，SA′E′B′F′取最大值，所以

图3.1

图3.2

感悟特殊四边形，容易求得其面积;非特殊四边形面积的解决，应充分挖掘其几何特征，如对角线相互垂直.更特殊的，椭圆内接四边形其中一条对角线过对称中心，则对应单位圆中它则为直径，这些都为为椭圆内接四边形面积的解决开辟了新的方向.

五、其它考题链接

1.(2016年高考四川卷文科第20 题(节选)) 已知椭圆=1(a ＞b ＞0)的一个焦点与短轴的两个端点是正三角形的三个顶点，点在椭圆E上.

(Ⅱ)设不过原点O且斜率为的直线l与椭圆E交于不同的两点A，B，线段AB的中点为M，直线OM与椭圆E交于C，D，证明:|MA|·|MB|=|MC|·|MD|.

(Ⅰ) 求椭圆C的方程; (Ⅱ) 求ΔAPB面积取最大值时直线l的方程.(参考答案: (Ⅰ)=1; (Ⅱ)

3.(2015年高考上海卷理科第21 题(节选)) 已知椭圆x2+2y2=1，过原点的两条直线l1和l2分别与椭圆交于A、B和C、D，记得到的平行四边形ACBD的面积为S.(Ⅱ)设l1与l2的斜率之积为求面积S的值.(参考答案: 2)

伸缩变换使得椭圆问题化归圆解决，如本文所述，当对应圆中图形涉及中点、斜率、长度、面积、平行、垂直等特殊几何关系时，先在圆的几何背景下求解问题，然后根据伸缩变换性质，还原到椭圆得到相应结论，能有效避免椭圆的繁杂代数运算过程，使得数形结合思想进一步深化.