合作探究 实验建模 能力提升
——以“锐角三角函数”单元复习课教学为例

■霍 燕

数学建模，是运用数学的语言和方法，通过抽象、简化，建立起能近似刻画并解决实际问题的模型。它是一种强有力的数学手段。简而言之，数学建模既是一种重要的数学思想方法，也是数学核心素养之一。数学课程标准指出，学习活动中需注重学生合作探究能力的培养。因此，在锐角三角函数的单元复习课教学中，教师应鼓励学生合作探究、实验建模，从而培养学生解决问题的能力及创新意识。

笔者认为，基础知识的了然于心是建模的前提，首先需理清基础知识；建立模型是学生的学习难点，而给予学生充分的时间合作实验有助于学生更好地讨论交流，是建模的有效方式；建立模型后的巩固也是至关重要的，因此需进一步练习，以便消化；建模最终是为了更好地解决实际问题，因此，回归问题的本质，利用模型，尝试解决实际问题也是很重要的一个环节。

一、夯实基础，提升建模信心

数学基础知识的牢固掌握是数学建模能力提升的前提，学生只有充分理解并掌握了相关的基础知识，方可更好地运用知识本质。因此，在教学中，教师需精心选择问题的切入点，从直击核心的简单问题出发，提升学生学习的积极性和建立下一步学习的信心。为了更好地培养学生的建模意识，在这节复习课的开始，笔者对教材内容进行了整合，从实际问题出发，展开教学。

案例1 锐角三角函数的简单运用

问题1如图1，小亮为了测量校园里教学楼AB的高度，将测角仪C D竖直放置在与教学楼水平距离为的地面上，若测角仪的高度为1.5m，测得教学楼的顶部A处的仰角为30度，求教学楼的高度。

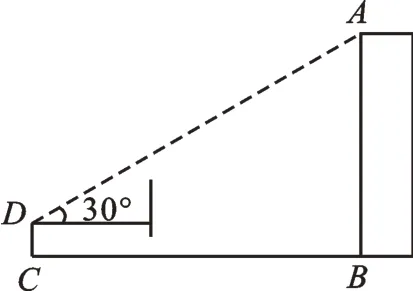
图1

从实际问题出发，将实际问题抽象成数学问题。模型一：在Rt△A B C中，已知∠C=90°，∠A=30°。结论1.若B C=x，则，AB=2x；结论2.若AC=x，则；结论3.若AB=x，则。将条件延伸至等腰直角三角形中，从而建立模型二：结论1.若斜边为x，则两直角边均为；结论2.若两直角边为x，则斜边为

此题给出了具体的图形，学生只需在图形中找寻解决问题的方法，实现建模学习的低起点。在教学中，教师引导学生说出特殊角的直角三角形中的边、角关系，通过比较所设未知数，学生容易得出结论；采用设最短边的长度的方法，可以更方便地求解问题，从而领会到理解基础知识本质特征的重要性。建模后问题的顺利解决，让学生觉得原来建模并不是高不可攀的复杂技能，提升了学习的积极性，为后续更复杂的建模尝试做正面的心理建设与铺垫。

二、合作实验，助力建模

建构主义认为，知识的获得依赖于学生自身已有的知识和经验，进而主动建构。因此，教师应放弃满堂灌及填鸭式的教学，而采用小组合作的形式组织教学。学生通过动手操作、自主探索、合作交流，从而达到建模、解模的目的。为了解决本节课的核心问题，笔者设计了如下实验活动，引导学生从实验出发，在实验活动中合作交流，得出实验结果，进而得出模型，解决问题。该环节既是本节课的重点，也是本节课的难点。笔者给予学生充分的时间操作、探究、合作、交流、质疑，最终构建出了初中阶段锐角三角函数这一章中最重要的六个基本模型。

案例2 实验活动及实验结果

问题2活动1.△AB C中，∠C=90°，∠A=30°，沿着过点C的直线折叠，折叠后点B落在线段A B上。若BC=1，思考：可以求出哪些线段的长度及哪些角的度数？

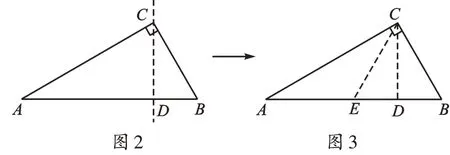
活动2.用两张三角形纸片拼接三角形（可重叠）。

操作：将图3纸片沿着CD剪下，得到△AD C与△C D B。若有Rt△C DM（C M为斜边，C D=DM），思考：将△AD C、△CDB、Rt△CD M重新拼接，能拼成一个新的三角形，则Rt△CD M（CM为斜边，CD=D M）有什么样的要求？请完成拼图，并写出实验结果。

通过两个实验活动，学生在实验合作过程中，建立如下6个模型（如图4所示）。

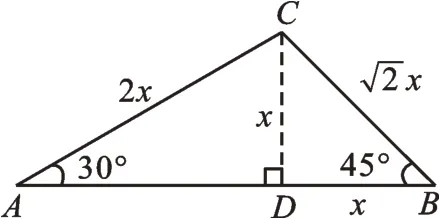
图4

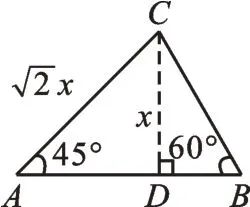
图5

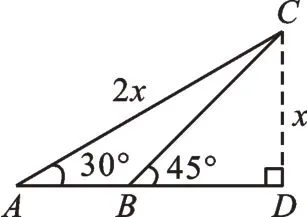
图6

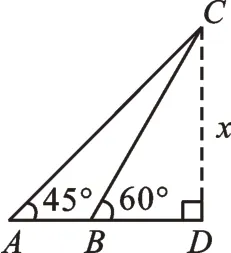
图7

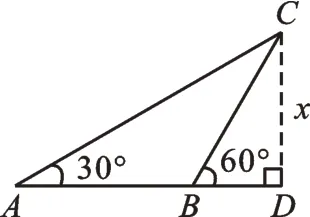
图9

学生发现在作出高CD后，如果设CD=x，那么含特殊角的斜△A B C所有边都可用含x的代数式表示出来，实现了解特殊斜三角形的目的。学生还感知到添高是解决问题的关键。另外，学生还在讨论交流中，得出了添哪条高更合适，实现了不破坏特殊角，构建含特殊角的三角形解决一类问题。基于案例1，有学生指出，设最短边来表示出的△ABC的各边更简单，例如在图8中，如果设B D=x，则，B C=2x，A D=3x，，AB=4x。学生感悟到今后遇到此类问题，未知数既可以直接设，也可以间接设，选取合适的方法，能使计算变得简便。

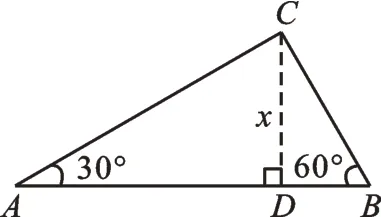
图8

学生在剪一剪、拼一拼的过程中，感受到通过动手实践可以得出结论。在合作交流中，学生思维火花的不断碰撞产生的精彩生成，不仅发展了学生的表达能力，更提升了小组的竞争意识与凝聚力。教师给予及时的点拨、评价有助于学生理解并反思。学生在“做”数学中思维得到拓展，创新意识和自主学习的能力得以进一步提升。

三、巩固提高，内化模型

通过实验活动的开展，学生得出了模型，而知识的灵活运用需要在已学的基础上进行巩固、变式练习，使数学学习从表层走向深层。在开展变式练习时，教师应鼓励并引导学生洞察变化的外在特征，发现并抽象出不变的内在结构。为了全面复习所得到的6个模型，笔者设计了如下开放性题目。

案例3 提出问题，强化模型

问题3如图10是一副学生用的三角板，在△ABC中，∠C=90°，∠A=60°，∠B=30°；在△A1B1C1中，∠C1=90°，∠B1A1C1=45°，∠B1=45°，且A1B1=CB。若将边A1C1与边CA重合，其中点A1与点C重合。将三角板A1B1C1绕点C（A1）按逆时针方向旋转，旋转角度为α，旋转过程中边A1C1与边A B的交点为M，设A C=a，两块三角板重叠部分的面积为S。若α为15°，试计算S。根据今天所学内容，你能再对α进行改变，并求出S吗？

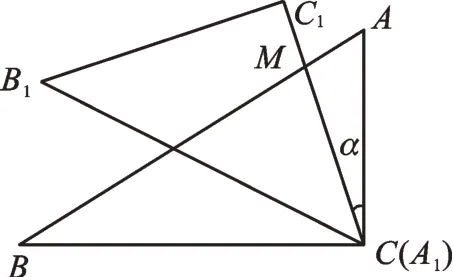
图10

在教学过程中，引导学生通过转一转三角板的方式加深对题目的理解与认识，体会图形运动的过程，接着对α角展开讨论，从特殊的角度出发，如30°，解决问题后，再次变换角度为45°、60°，最后学生发现解决这些特殊角的问题，只需找出6个模型，所有问题就能顺利解决，再次感悟到建模的重要性。甚至还有学生指出如果α角是一般角，也能利用之前的方法解决问题，区别在于涉及参数多了，还要对α角的范围进行讨论。该名学生还大胆预测，如果得出了一般模型的答案，那么之前的特殊角问题就只需要完成代数式求值即可。笔者表扬并肯定其提出了一个极其价值的问题，鼓励其他学生参与进去，课后再进行深入思考，以期得到上述6个模型的一般公式。

四、回归实际，运用模型

当学生经历了从简单建模到复杂建模，再到模型的巩固运用这一过程后，就基本具备了计算三角形边的能力。历史上三角函数的产生是基于对测量的需求。数学来源于生活，又服务于生活。

案例4 实际问题，创意解决

问题4课后拓展：请同学们利用所学知识测量学校的旗杆高度。

将现实生活的问题带到数学课堂中，引导学生积极动脑、勤于动手，在利用建模解决问题的过程中，培养了学生对知识的迁移能力，让他们用数学的眼光来研究问题，体现数学的实用价值。课后的拓展题，学生贡献出了多种测量学校旗杆高度的方法，让人再次感受到数学建模的魅力。

“实战演练”加深了学生对知识的理解，有助于学生建构属于自己的知识结构，一定程度上激发了学生的学习动机，缓解了数学学习过程中的枯燥乏味，学生运用数学的意识得以培养，最终提升了学生的创造性思维和可持续发展素养。

本课时的设计与实施，建立在学生已有的学习基础上，笔者对教材中的核心知识点进行了整合。学生在数学建模时经历了从无到有的过程，从简单基础走向高阶思考，思维得到进阶。

通过这节课的尝试，我们看到了孩子们智慧火花的飞溅，看到了孩子们对知识的渴求，感受到数学不仅拥有“冰冷的美丽”，还能绽放灵动的色彩。

在今后的教学中，需不断整合合适的教学资源，在课堂中注意对学生数学建模能力的培养，引领学生直击知识的精髓，培养学生的数学建模意识、数学模型思想，进而提高学生“学好数学”“用好数学”的能力。