基于MM-GGIW-PMBM 滤波的扩展目标跟踪算法

吴孙勇, 周于松, 谢芸, 蔡如华, 樊向婷

(1. 桂林电子科技大学 数学与计算科学学院, 桂林 541004; 2. 广西精密导航技术与应用重点实验室, 桂林 541004)

多目标跟踪(multiple target tracking, MTT)的目的是从一系列有噪声、带有杂波的测量数据中检测和跟踪目标。 在大多数应用(如雷达)中,由于目标和传感器之间的距离较远或者传感器分辨率过低,目标被看作是点目标,每个点目标在每个时间间隔内最多产生一个测量值。 然而,随着传感器的分辨率越来越高,目标将占据传感器的多个分辨率单元,使得单个目标在每次扫描时会产生多个量测,从而点目标的模型假设就不再成立,此时则需要将目标模型建模为扩展目标。 区别于传统意义上的点目标,扩展目标的演化是递归估计目标外形和运动状态的过程,每个目标在每个时刻可能会产生多个量测,其详细的概述在文献[1]中给出。

在贝叶斯框架下,Mahler[2]将随机有限集(random finite set, RFS)应用于MTT 问题之中,早期基于RFS 的MTT 算法通过逼近后验多目标密度的一阶矩来跟踪目标,如概率假设密度(probability hypothesis density, PHD)滤波器[3-5]和势概率假设密度(cardinality PHD,CPHD)[6-7]滤波器。 而近年来基于RFS 的共轭MTT 问题引起了广泛的关注,MTT[8]中的共轭性意味着所有的先验和后验概率密度都具有相同的函数形式,即通过共轭先验可以为目标概率密度提供闭式解,理论上保证了最优。

在文献中可以找到2 种类型的多目标滤波满足共轭先验的性质:广义标签多伯努利滤波(generalized labeled multi-Bernoulli filtering, GLMB)[8-9]和泊松多伯努利混合滤波(Poisson multi-Bernoulli mixture filtering, PMBM)[10]。 相较于GLMB,PMBM的滤波精度更高且计算代价更小。 PMBM 滤波允许将扩展目标集合划分成2 个不相交的子集:已检测到的目标集合和还没有被检测到的目标集合。 文献[10]提出了一种GGIW-PMBM 滤波算法,该算法假设目标状态服从伽马高斯逆威夏特(Gamma Gaussian inverse Wishart,GGIW)分布[11],通过单一的运动模型对扩展目标的演化进行建模,然而当该运动模型无法与目标运动相匹配时,就会导致跟踪精度下降。

在Granström 等[10]提出的GGIM-PMBM 多机动扩展目标跟踪算法中,本文结合交互式多模型[12-14](interacting multiple model, IMM)算法的思想,提出了一种多模型的GGIM-PMBM (MMGGIW-PMBM) 算法。 首先,在预测阶段利用IMM算法融合多种运动模型,实现对扩展目标的混合估计;然后,引入强跟踪滤波器(strong tracking filter, STF)的渐消因子,使输出残差正交,增强算法对目标的跟踪能力和估计精度,使得当扩展目标在做机动运动时,能够快速地为目标匹配准确的运动模型;最后,在PMBM 更新阶段利用似然函数完成模型概率的更新。 此外,本文采用广义最优子模式[15](generalized optimal sub-pattern assignment, GOSPA)距离衡量算法的跟踪性能,该方法将误差分解成目标位置误差、漏检目标数量和误检目标数量3 部分,能够直观地展现扩展目标跟踪算法的性能。

1 模型框架

假设在k时刻将扩展目标建模为

式中:Nx,k为k时刻目标的数量;为第i个目标的泊松分布量测比率;为第i个目标质心的运动学状态,包含目标的位置、速度及转弯率等参数;为第i个目标的外形状态,包含目标的形状和大小。 将扩展目标建模为RFS,根据RFS 的性质,目标的势(Nx,k)为时变离散随机变量,目标的状态()为随机变量。

利用线性高斯动态模型[16]为多运动模型下目标的质心建模,即

式 中:M为 转 移 模 型 总 数 量;为 第r个 模 型的转移概率;为第r个转移模型对应的过程噪声,其均值为0,协方差为;为第r个模型对应的转移矩阵;Id为单位矩阵,d为目标外形的维度;“⊗”表示克罗内克积。

假设Zk=为k时刻的量测集,其同样被假设为RFS,通过线性高斯模型建模,可表示为

量测集合Zk由杂波量测和目标产生量测的并集组成,表示为

式中:θ(z)为由目标产生的量测;k(z)为杂波量测,假设它们相互独立。 杂波量测k(z) =λc(z),λ为杂波量测数量对应的泊松率,c(z)为杂波的空间概率分布函数。

设扩展目标的状态ξ的检测概率为pD(ξ),如果被检测到,产生的量测数量服从泊松分布,密度为γφ(),γ为目标产生的量测数量对应的泊松率,φ(z|ξ)为依赖目标状态的量测分布函数。 则对于非空量测集(＞0),其似然函数可表示为

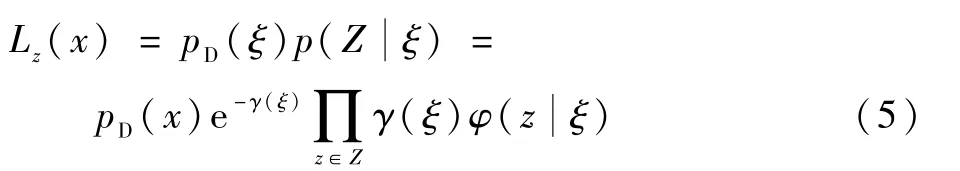
式中:p(ξ)为预测似然函数。 因为量测服从泊松分布,所以目标至少产生一个量测的概率为1 - e-γ(ξ),则 扩 展 目 标ξ的 有 效 检 测 概 率 为pD(ξ)(1- e-γ(ξ)), 漏检的概率可以表示为

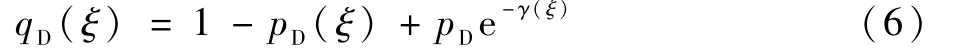
注意,qD(ξ)同样也是量测集合为空集时的条件似然,即Lz=∅(ξ) =qD(ξ),∅为空集。

2 扩展目标状态的概率密度分布

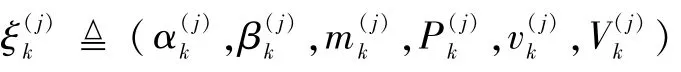
式中:Γ(·)为伽马函数。

x～N(x;m,P)表示质心的运动学状态分布,m为均值,P为协方差。

式中:etr(·) =exp(tr(·))表示矩阵迹的指数;Γd为多元伽马函数。

根据式(7) ～式(9),扩展目标状态数服从GGIW 分布,表示为

式中:ξ≜(γ,x,X) 为扩展目标待估计状态,ξ≜(α,β,m,P,v,V)为GGIW 的分量参数。

3 泊松多伯努利混合滤波

3.1 泊松点过程

泊松点过程(Poisson point process, PPP)假设RFS 中目标数量服从泊松分布,且目标状态之间独立同分布。 PPP 可通过单目标状态空间中的强度函数D(x)参数化,而强度函数D(x)可由未知目标数量对应的泊松率μ与扩展目标的分布函数f(x)的乘积表示,即D(x) =μf(x)。 此外,强度函数还具有一个重要的性质,即空间S中扩展目标的总数量可以由∫x∈SD(x)dx表示。 通过强度函数D(x),PPP 的密度可表示为

3.2 多伯努利混合过程

伯努利集合XB同样为RFS,且集合XB中包含的变量最多只能有一个,其概率密度函数为

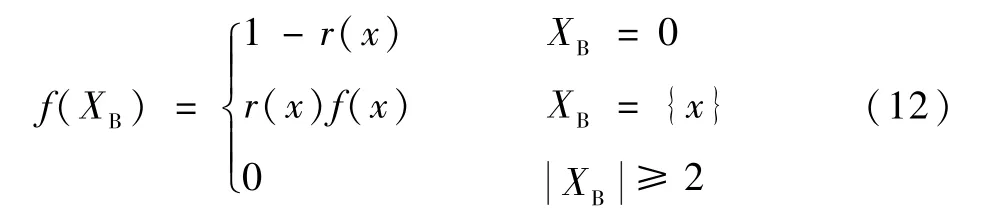
式中:r(x)为存活概率;f(x)为概率密度函数。在MTT,伯努利RFS 包含了单个目标存在情况的不确定性(通过r(x))和目标状态x的不确定性(通过f(x))。

多伯努利(multi Bernoulli, MB)RFSXMB是固定数量的伯努利RFS(n∈Π,Π为索引集)的并集,可表示为

集合XMB概率密度函数为

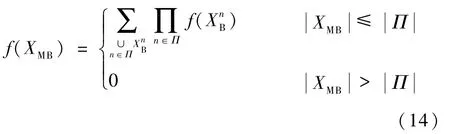
MB 的分布可通过其伯努利参数{r(x),f(x)}Π表示。

多伯努利混合(MB mixture, MBM)密度可以由一系列正则化且带有权重的MB 的概率密度函数混合表示,即MBM 可以由{(ωs,{rs,n(x),fs,n(x)}n∈Πs)}s∈J定义,其中,J为MBM 中MB 的索引集合,Πs为第s个MB 中伯努利成分的索引集合,ωs为第s个MB 的权重。

3.3 PMBM 结构

PMBM 可以用2 个部分表示:一部分为PPP,用来估计多目标演化过程中存在但是并未被检测到的目标,由符号Xu表示;另外一部分为MBM,用来估计多目标演化过程中已经被检测到的目标的分布情况,由符号Xs表示。 因此,目标集合X可以划分成2 个不相交的子集:

PMBM 密度函数可表示为

式中:fs,n(·)为第s个MB 中第n个伯努利的密度函数;设rs,n(·)为第s个MB 中第n个伯努利的存活概率,每个伯努利成分由GGIW 成分混合表示;为MBM 中MB 的数量;Πs为第s个MB 分量中伯努利的数量;Du为未知目标的强度函数。

则PMBM 可以通过参数表示为:Du,{(ωs,{rs,n(x),fs,n(x)}n∈Πs)}s∈J。

3.4 PMBM 滤波的递归算法

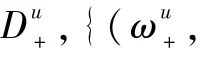
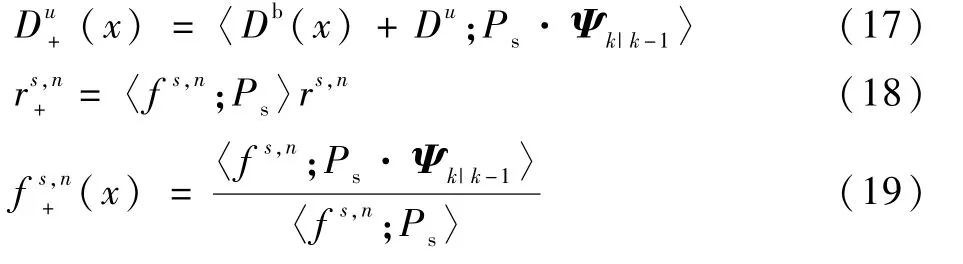
式中:Db(x)为新生分量强度函数;Ps为目标存活概率;Ψk|k-1为转移矩阵的混合估计;=ωs。

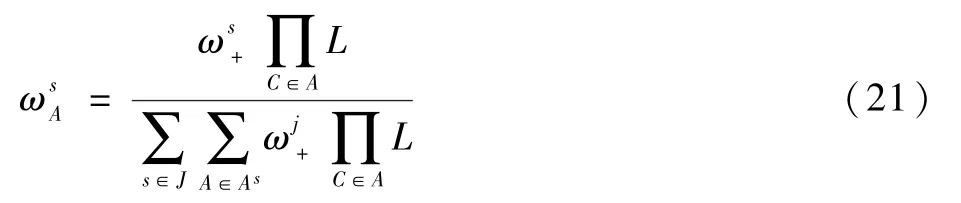
其中:L表示似然函数;A为伯努利成分的数据关联;As为第s个MB 的数据关联集合。

PPP 的密度Du为

4 MM-GGIW-PMBM 的递归

多模型PMBM 算法与单模型PMBM 算法的区别主要在预测阶段。 因为扩展目标的概率密度函数可由式(10)表示,所以可以通过对参数α、β、m、P、v、V的预测来对GGIW 变量进行预测。 而多模型PMBM 算法在预测阶段需要对参数α、β、m、P、v、V进行混合估计预测,且还要使用STF 修正预测之后的GGIW 的协方差,MM-GGIW-PMBM预测阶段算法如下:

4.1 多模型GGIW 分量预测阶段的混合估计

式中:M为运动模型的总数量;ηk-1,r为第r个模型下指数渐消因子;为k- 1 时 刻 第j个GGIW 分量对应第r个模型的概率;πir为模型i到模型r转移概率;τk-1,r为扩展目标在第r个模型下的扩展灵敏度;T为采样时间间隔;为第r个模型 对应 的 转 移 矩 阵;为 第r个 模 型 对应的过程噪声协方差。

4.2 强跟踪滤波器修正

由于扩展目标跟踪算法对转移矩阵模型有非常严格的要求,当实际转移模型参数发生变化时,会使滤波器的状态估计出现较大偏差。 因此,通过引入一种STF,利用时变的渐消因子在线实时调整增益矩阵,从而自适应修正协方差,增强算法对机动目标的跟踪能力。 第j个GGIW 分量的预测协方差的修正公式如下:

式中:Rk为量测噪声协方差;Hk为量测矩阵;为第j个扩展目标的外形参数预测;λ0为弱化因子;为量测子集的数量。

4.3 GGIW 分量的更新

多模型PMBM 算法与单模型PMBM 算法在更新阶段的区别在于多模型PMBM 算法需要对模型概率进行更新,MM-GGIW-PMBM 更新阶段算法如下:

同时在更新阶段完成模型概率的更新。 假设模型的总数量为M,则对于新生目标分量的模型概率为

未检测到的目标分量和已检测到的目标分量的模型概率更新方式相同,其模型概率为

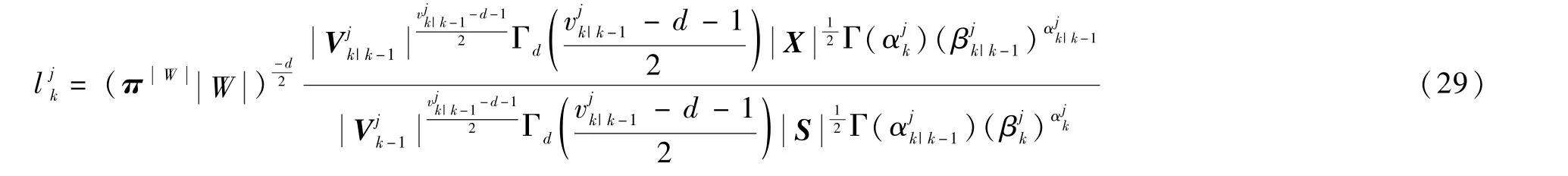
5 仿真实验

5.1 性能评估

对于椭圆外形扩展目标估计的性能评价主要有6 种[17],其中,基于高斯Wassterstein 距离(Gaussian Wassterstein distance, GWD)[18]通常是最佳的选择,而本文则是选择文献[15]中GOSPA多目标度量对所提算法进行评估,其定义为

5.2 仿真场景

在算法实验场景中,假设目标的运动方式有2 种,分别为匀速直线(CV)转弯(CT)运动,对应的模型转移矩阵为

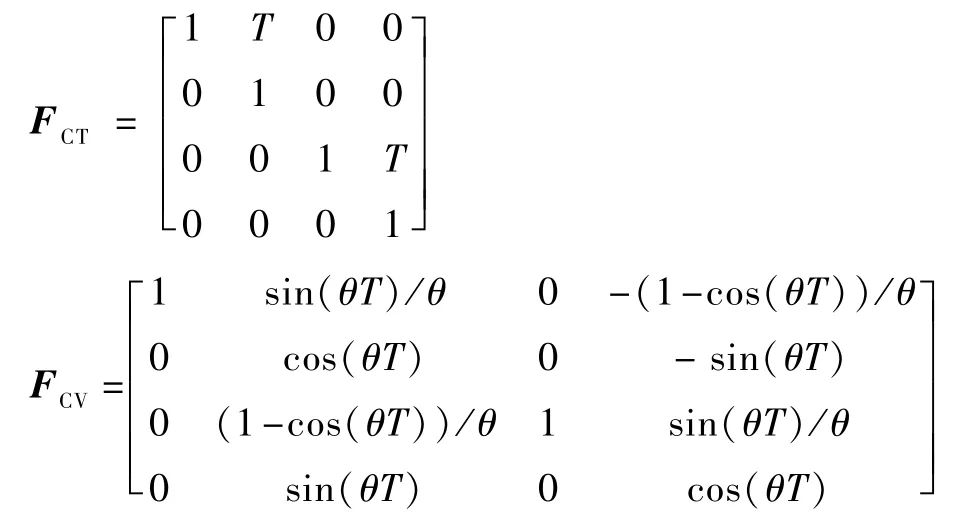
其对应的过程噪声分别为

式中:T=1 s 为时间采样间隔长度。 STF 的弱化因子λ0=1,扩展目标的检测概率Pd =0.8,存活概率Ps =0.99,杂波服从均值为60 的泊松分布,模型i到模型r转移概率矩阵为

5.3 算法性能对比

在图1 和图2 中,存在3 个扩展目标在设定的杂波环境中运动。 第1 个目标质心的初始运动信息为[ - 75 m; - 2 m/s; - 75 m;2 m/s],在1 ～5 s做匀速直线运动,在6 ～20 s 做角速度为-0.2 rad/s的转弯运动,在21 ～30 s 做角速度为0.3 rad/s 的转弯运动。 第2 个扩展目标质心的初始运动信息为[ -75 m; -2 m/s;75 m;2 m/s],在10 ～14 s 做匀速直线运动,在15 ～20 s 做角速度为-0.2 rad/s 的转弯运动,在21 ～30 s 做角速度为0.3 rad/s 的转弯运动。 第3 个扩展目标质心的初始运动信息为[75 m;2 m/s;75 m;2 m/s],在7 ～11 s 做匀速直线运动,在12 ～20 s做角速度为-0.2 rad/s 的转弯运动,在21 ～30 s做角速度为0.3 rad/s 的转弯运动。 3 个扩展目标的椭圆外形的长短轴相同,分别为0. 8 m 和1 m,初始概率分别为[1/3,1/3,1/3],各运动模型对应伽马分布指数的渐消因子分别为2、2、3,而外形随时间变化的灵敏度分别为τ=9、10、10,图1 采用的是MM-GGIW-PMBM 算法,图2 采用的是GGIW-PMBM 算法。 可以看出,相较于采用单个运动模型的GGIW-PMBM 算法,MM-GGIWPMBM 算法对扩展目标的估计更加精确稳定。

图1 MM-GGIW-PMBM 算法下扩展目标运动轨迹及其估计轨迹Fig.1 Trajectory of extended target and its estimated trajectory by MM-GGIW-PMBM algorithm

图2 GGIW-PMBM 算法下扩展目标运动轨迹及其估计轨迹Fig.2 Trajectory of extended target and its estimated trajectory by GGIW-PMBM algorithm

为了进一步验证本文算法的精度及有效性,将MM-GGIW-PMBM 算法与相同条件下的MMGGIW-PHD 算法做对比,一共进行100 次蒙特卡罗实验取估计误差均值,且每一次实验目标运行100 个时刻,共对27 个目标进行跟踪,目标出生及消失的时刻各不相同,在第58 个时刻之前跟踪的目标数量较少,第58 个时刻之后目标数量较多。

图3 和图4 分别为目标数量的估计及目标数量误差的估计。 可以看出,在第58 个时刻之前,由于目标数量较少,MM-GGIW-PMBM 算法估计精度只是略高于MM-GGIW-PHD 算法,但在第58个时刻之后,目标数量增多,MM-GGIW-PHD 算法估计误差出现大幅度波动,而MM-GGIW-PMBM算法估计误差则保持稳定,这是因为PHD 滤波通过泊松分布近似目标的数量分布,但是由于泊松分布的均值与协方差相等这一特性,即目标数量过多时,其估计的误差也会随之增大。

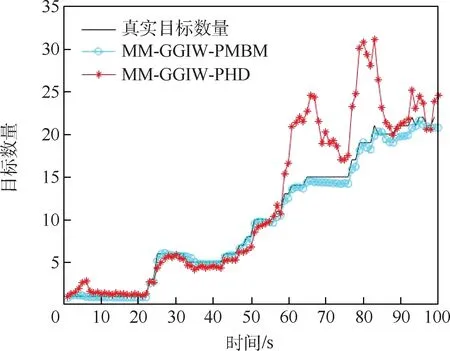
图3 两种算法对目标数量的估计对比Fig.3 Comparison of two algorithms for estimating target numbers

图4 两种算法对目标数量的估计误差对比Fig.4 Comparison of two algorithms for estimating error of target numbers

由于GOSPA 算法的特殊性,可以将GOSPA误差分为目标位置误差、漏检目标数量及误检目标数量3 部分。 其中,2 种算法GOSPA 距离估计的误差如图5 所示,即扩展目标位置误差、漏检目标数量及误检目标数量总体误差对比;图6 为2种算法对目标位置估计的误差;图7 为2 种算法对漏检目标数量的估计;图8 为2 种算法对误检目标数量的估计。 从图5、图7 和图8 中可以看出,当目标数量较少时,相较于MM-GGIW-PHD算法,虽然MM-GGIW-PMBM 算法对扩展目标的GOSPA 距离误差、漏检目标数量及误检目标数量估计更加精确稳定,但这种优势并不明显,甚至对目标位置的估计(在图6 给出)精度还要略低于MM-GGIW-PHD 算法。 而当目标的数量较多时,随着量测信息的积累,MM-GGIW-PMBM 算法在GOSPA 距离误差、漏检目标数量及误检目标数量这3 方面的估计精度要远强于MM-GGIW-PHD算法,其对目标位置的估计精度也强于MMGGIW-PHD 算法。

图5 两种算法GOSPA 距离估计误差对比Fig.5 Comparison of GOSPA distance estimation errors between two algorithms

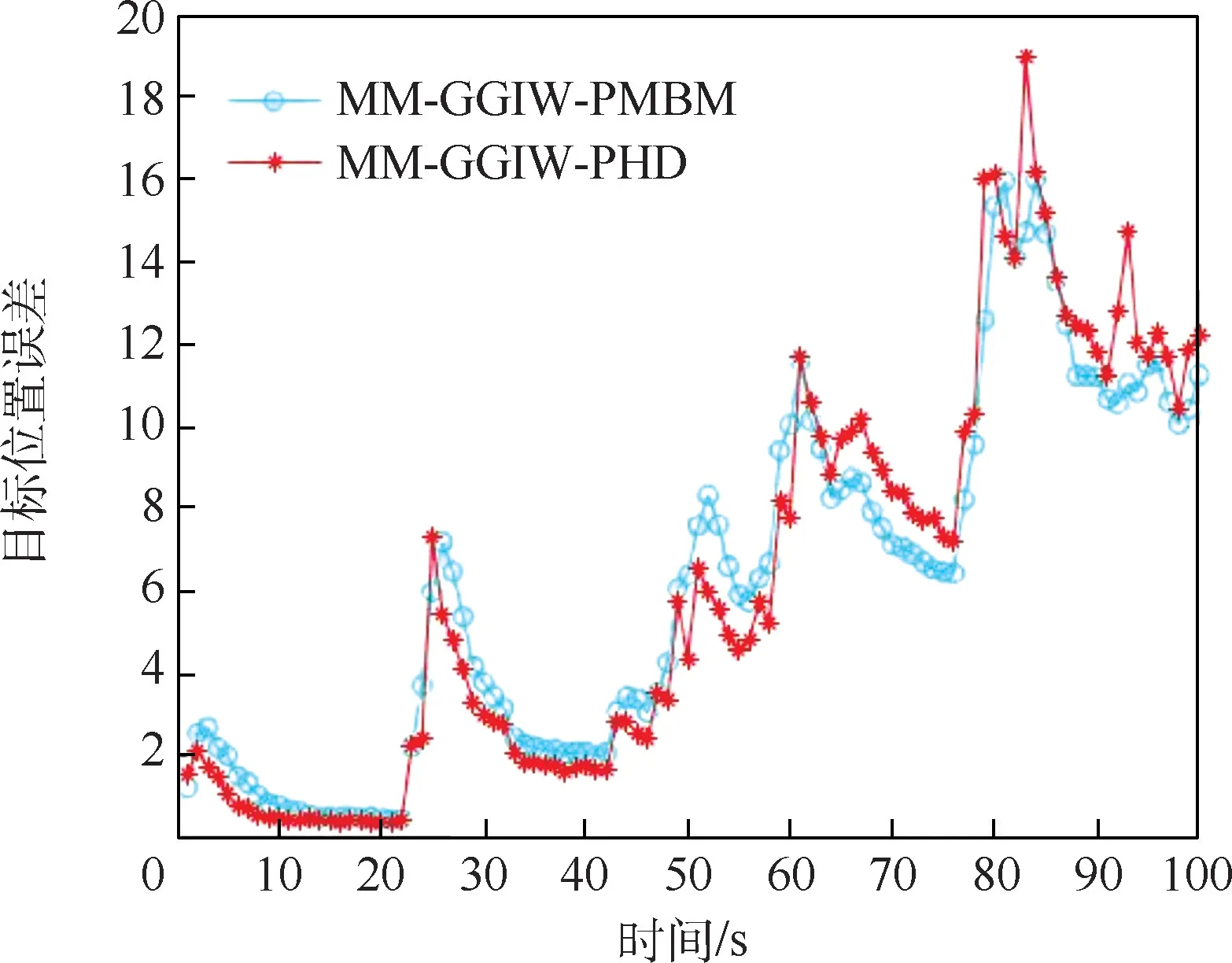
图6 两种算法目标位置估计误差对比Fig.6 Comparison of target location estimation errors between two algorithms

图7 两种算法漏检目标数量估计对比Fig.7 Comparison of estimating missed target numbers between two algorithms

图8 两种算法误检目标数量估计对比Fig.8 Comparison of estimating false detection target numbers between two algorithms

6 结 论

1) 针对扩展目标的机动问题,提出了一种MM-GGIW-PMBM 算法,利用随机矩阵法将扩展外形建模成椭圆,再使用GGIW 分量描述扩展目标状态。

2) 仿真结果表明在扩展目标的交互式算法中引入强滤波跟踪的有效性,在相同条件下,当目标做机动运动时,传统的单模型GGIW-PMBM 算法会逐渐跟丢目标,不能对多机动扩展目标进行有效的估计,而MM-GGIW-PMBM 算法在目标做机动运动时能够快速做出调整。

3) 相较于MM-GGIW-PHD 算法,当目标数量较多时,MM-GGIW-PMBM 算法能够更加稳定有效地对目标进行估计。