地月空间的远距离逆行轨道族及其分岔研究

陈冠华, 杨驰航, 张晨, 张皓,*

(1. 中国科学院空间应用工程与技术中心 太空应用重点实验室, 北京 100094; 2. 中国科学院大学, 北京 100049)

地月空间是近地轨道与月球轨道之间的空间区域,拥有丰富的战略资源。 近年来,地月空间逐渐受到关注。 2017 年,NASA 提出将在未来十年内建立一个连接地月空间与深空的空间运输网络[1]。 对于深空中长期执行的科学研究任务,稳定及近似稳定的轨道,如远距离逆行轨道(distant retrograde orbit, DRO)、近直线晕轨道(near-rectilinear halo orbit, NRHO)及三角平动点轨道(triangular libration points orbits),是这类任务的潜在应用轨道。 NASA 已经提出了在围绕月球的NRHO 轨道上部署深空门户空间站的方案[2]。 在NASA 的小行星重定向任务(ARM)中,航天器与近地小行星交会并将其捕获至地月系统DRO 上,如此小行星能够长期维持轨道稳定而不需要施加控制[3]。

DRO 是圆型限制性三体问题(circular restricted three-body problem, CR3BP)中的一类特殊周期轨道。 地月系统的DRO 位于月球公转平面,绕月逆行,其运动范围广,有着高度稳定性,对地球和月球都有良好的覆盖性,因而是本文关注的重点。

过去数年,学者们对地月空间、日地系统及其他CR3BP 系统的DRO 轨道特性、轨道转移和应用方案进行了一系列的研究。

在DRO 的轨道特性方面,目前学者的理论研究主要集中在轨道有界性、稳定性、摄动力影响及延拓求解等方面。 对地月空间的DRO,Bezrouk等[4-5]研究了地月系统中摄动力对DRO 的影响,证明了大幅值DRO 的轨道稳定性主要由太阳光压影响,而小幅值DRO 的轨道稳定性主要由月球固体潮所影响;彭超等[6]利用延拓求解DRO 共振轨道,并分析了其非开普勒特性与轨道稳定性;吴小婧等[7]研究了DRO 在实际力学环境中的摄动,发现太阳引力、月球偏心率是主要的摄动因素,为DRO 的精确建模和标称轨道设计奠定了一定的理论基础。 对火星系统的DRO,陈泓儒等[8]研究了在火卫一附近如何设计具有期望稳定特性和观测特性的有界轨道,并验证了稳定性水平。

在DRO 的轨道转移方面,目前学者的理论研究集中在DRO 与地球低轨道(low Earth orbit,LEO)、NRHO、深空轨道等轨道之间的低能耗转移。 在地月空间中,Capdevila 等[9-10]利用脉冲机动实现从LEO 到DRO、从DRO 到周边的周期轨道,以及DRO 与NRHO 之间的转移,并将有代表性的解转化到星历模型,比较了任务成本;张瑞康等[11]研究了从DRO 向轨道倾角为0° ～90°的月球低轨道之间的转移,对转移路径进行了分类,并比较了脉冲成本和飞行时间;曾豪等[12]研究了NRHO 与DRO 的低能往返轨道转移在月球探测中的应用,结合天体借力飞行技术和混合优化技术系统分析了关键参数的影响,给出了往返轨道设计初值的选择策略。 在深空转移方面,Cavallari等[13]研究了从地月系统DRO 到火星的低能耗转移;Conte 和Spencer[14]设计了从LEO 出发进入火星系统DRO 轨道的转移方案,并探讨了地月系统DRO 作为中转站的可行性;Scott 和Spencer[15]计算了从LEO 到日地系统DRO 的转移轨道族;Ocampo 和Rosborough[16]研究了使用脉冲和连续推力从近地停泊轨道转移到日地系统DRO 的能量。

在DRO 的轨道应用方面,对地月空间的DRO,徐明和徐世杰[17]提出在DRO 上放置中继卫星的概念;王文彬等[18]将DRO 用于深空自主导航,提出在DRO 卫星与另一个卫星之间进行星间测距以确定绝对轨道状态,并给出了动态模型误差和星载时钟误差下的导航性能评估。 对其他系统的DRO,Ocampo 和Rosborough[16]提出了在日地系统DRO 上部署太阳风暴预警系统等应用;在木星冰封卫星任务中,木星系统DRO 为航天器在木卫二欧罗巴周围的逃逸和捕获提供了瞬时稳定的转移路径[19];在欧洲航天局的DePhine 任务中,火星系统DRO 被用作该项目中火卫一与火卫二基地的备选轨道之一[20-21]。

可以看出,尽管目前与DRO 的应用相关的研究有很多,但对DRO 的轨道基础特性研究仍待完善。 由于DRO 的稳定性,长期的轨道保持所需的燃料成本较低,但其缺乏双曲流形结构,进出DRO 轨道附近区域的转移轨道的设计会受到一定制约,并可能需要更高的燃料成本;另外,由于DRO 位于小天体绕大天体的公转平面内,其应用受到了该平面的诸多限制。 因此,对DRO 附近动力结构的进一步探索,有助于深入了解该区域复杂的轨道特性和设计转移轨道。 例如,由于分岔成三维的DRO 轨道族具有平面外法向振幅,可用于规避日食、保持和地球连续通信等,其应用范围更广,而多周期DRO 的周边可能存在流形结构,因此通过DRO 轨道族的分岔研究其附近的周期性结构,能为轨道转移提供很大的设计便利。 为此,本文探讨了地月系统DRO 轨道族的相关特性。 首先,给出了动力学模型、周期轨道和流形的计算方法、稳定性理论相关的理论知识;然后,研究了DRO 轨道族的分岔、稳定性及周边的流形结构;最后,讨论了不同分支平均轨道周期与能量的关系。

1 周期轨道与流形计算

1.1 圆型限制性三体问题

采用CR3BP 进行建模。 在该近似模型中,地球P1与月球P2围绕其公共质心做圆周运动,航天器P3受地月2 个主天体引力的影响。 在图1 所示的旋转坐标系中,原点O设在P1和P2的共同质心,x轴沿P1指向P2,z轴与系统角动量方向平行,y轴由右手定则确定。 本文将其无量纲化处理:2 个主天体质量m1+m2= 1,定义μ=m2/(m1+m2)为系统质量参数,则通过计算可知:m1=1 -μ,m2=μ。P1和P2的位置坐标分别为( -μ,0,0)和(1 -μ,0,0)。

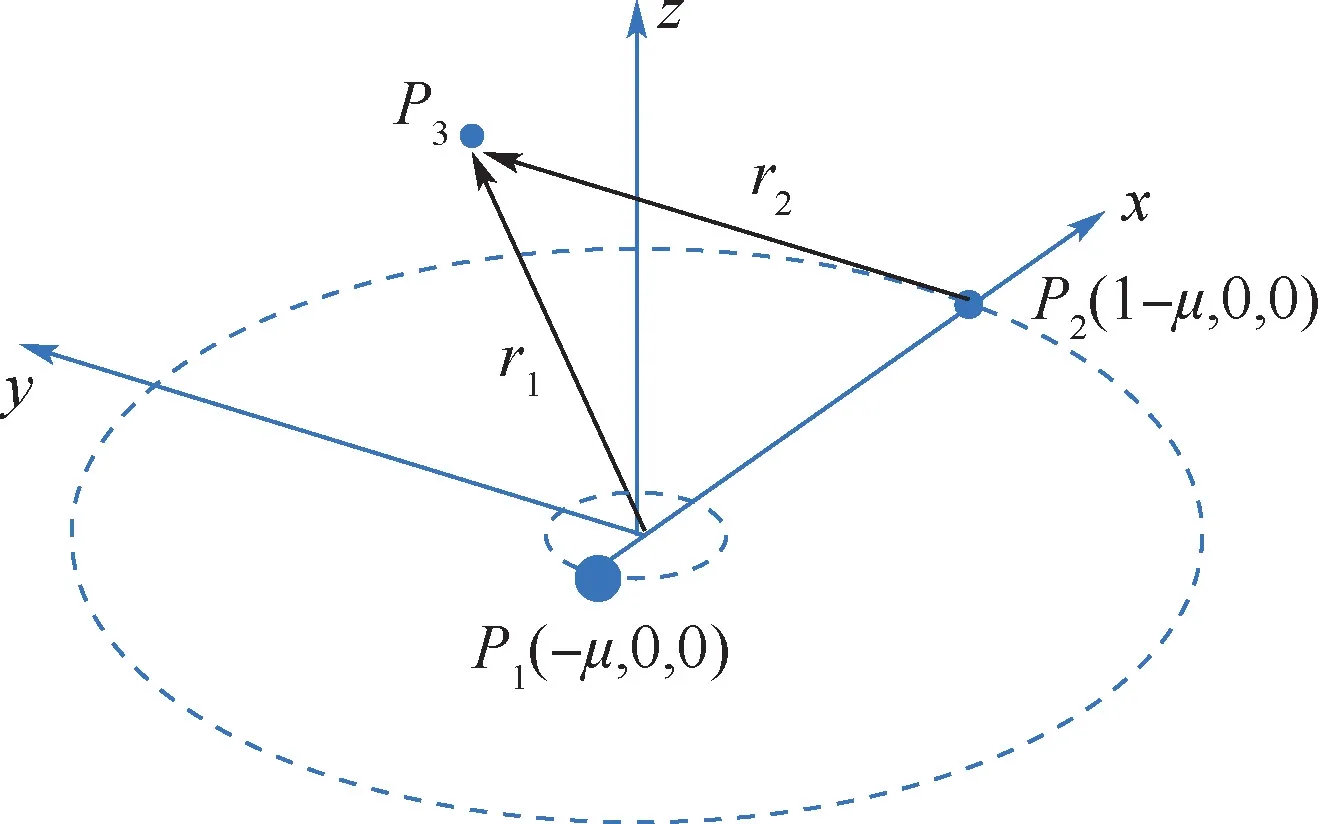
图1 圆型限制性三体问题Fig.1 Circular restricted three-body problem

在上述系统中,航天器P3的状态矢量为x=[x,y,z,vx,vy,vz]T,其动力学方程可表示为[21]˙x=f(x)=

式中:r1= [(x+μ)2+y2+z2]1/2;r2= [(x+μ-1)2+y2+z2]1/2。

在天体力学中,定义系统能量的-2 倍为雅可比积分常数J,数学表示为[22]

1.2 周期轨道的微分修正与数值延拓

记方程(1)的解为xt=φ(x0,t), 表示从初始状态x0运动t时间后的状态。 则方程(1)的周期解需要满足:

式中:T为轨道周期。 求解周期解实际上即为求解满足式(3)的轨道初值x0与周期T。

一般采用庞加莱截面降低式(3)的维度,庞加莱截面是多维相空间中的一种广义曲面,动力系统中连续的轨迹映射在庞加莱截面上表现为同性质的离散的点[23-24]。 由于DRO 轨道族在旋转系中关于x-z平面对称,本文选取平面y=0 作为庞加莱截面。 需注意,在计算轨道周期T时,单周期轨道的周期T为穿越一次庞加莱平面的时间,而N-周期轨道的周期T为穿越N次庞加莱平面的时间。

对平面周期轨道的求解,在应用庞加莱截面后,维度降低的迭代初值记为w= [x0,vy,0]T,对应的周期轨道初值为x0= [x0,0,0,0,vy,0,0]T。此时,周期轨道需要满足的式(3)改写为

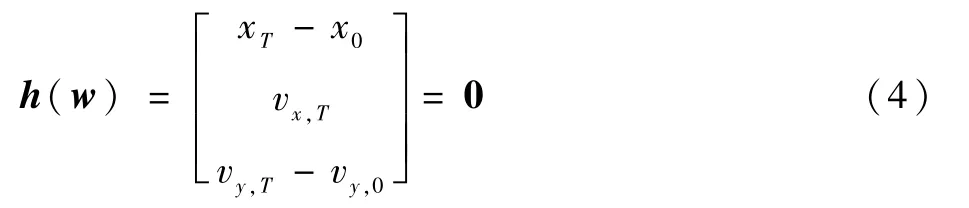
式(4)可以通过牛顿迭代法进行求解。 在求出一个周期解之后,就可以进行数值延拓,求解得到整个周期解族。 在延拓时,选择合适的延拓参数(本文选择轨道能量J),延拓初值可以由式(5)预测:

式中:k为周期轨道族中的轨道编号。

对三维周期轨道的求解,在应用庞加莱截面后,维度降低的迭代初值记为w= [x0,z0,vy,0]T,对应的周期轨道初值为x0= [x0,0,z0,0,vy,0,0]T。 此时,周期轨道需要满足的式(3)改写为

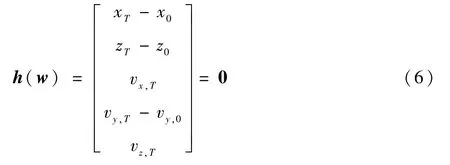
对式(6)的延拓求解时,选取参数为z。 延拓方程如下:

周期解求出之后,求解其变分方程就可以得到其单值矩阵M。M是该周期轨道一个轨道周期的状态转移矩阵,数学表示如下[25]:

满足初始条件M(0) =I。

1.3 流形的计算

由单值矩阵M的特征值对应的特征向量所张成的空间称为该系统的不变流形。 在CR3BP中,周期轨道单值矩阵M的特征值集C具有如下形式[25]:

式中:λ1＜1 为系统的稳定特征值,对应的特征向量v1产生了稳定流形;1/λ1＞1 为系统的不稳定特征值,对应的特征向量v2产生了不稳定流形。由于稳定流形和不稳定流形关于x-z平面对称,在得到稳定流形后通过翻转即可得到不稳定流形[22]。

记对应稳定流形和不稳定流形的特征向量分别为vs和vu。 沿着vs方向给一个小扰动ε,得到稳定流形的积分初值:

式中:xp为周期轨道的初值;在地月系统中一般取ε=50 km;“ ±”表示沿x轴正负方向稳定流形的2 个分支。 对xs数值积分即可得到xp初值对应稳定流形上的2 条轨道。 对周期轨道均匀取若干个离散点,分别按照上述方法计算其轨道,则可以绘制出该周期轨道的流形结构。

对于多周期轨道等几何形状较为复杂的轨道,直接绘制其流形会显得杂乱,不利于后续分析。 因此,仍采用庞加莱截面的方式呈现流形,即定义一个庞加莱截面,记录流形穿越该截面的坐标。 一个周期轨道的流形将会在该截面上构成一个或多个封闭的形状。

2 稳定性理论

衡量轨道稳定性的指标是稳定性指数,定义为

式中:λi为单值矩阵M的特征值,i=1,2,3。 若所有稳定性指数vi= 1,则该轨道线性稳定,并具有稳定子空间;若任何一个稳定性指数vi＞1,则轨道不稳定,轨道存在稳定及不稳定流形[25]。

在CR3BP 下,非平凡(不为1)的特征值的特征方程有以下形式[26]:

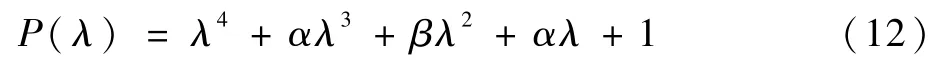
式中:α与β可由单值矩阵M与周期T计算得出:

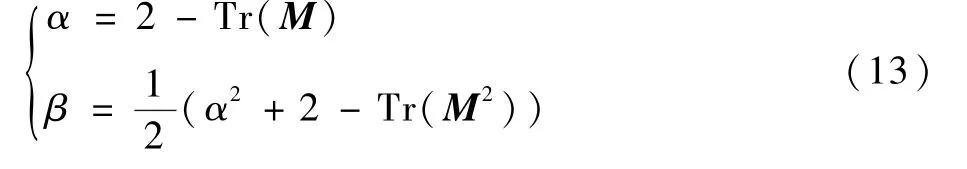
求解特征方程P(λ) =0 可得λi,从而可以判断周期解的稳定性。 实际上,可以通过直接观察α和β的值而得到周期解稳定性情况,而不必求解四次方程P(λ) =0。

稳定性与α-β的几何关系称为Broucke 图,如图2 所示[26]。 Broucke 图中有3 条关键曲线:β= -2α-2,β=2α-2,β=α2/4 +2。 这3 条曲线将α-β参数空间分为若干区域,每一个区域对应了不同的稳定性。 中心区域内部所代表的特征值都在复平面单位圆上,表示轨道稳定,而其余区域均有不稳定流形。 同一周期轨道族在Broucke图中体现为一条连续曲线,该曲线与上述关键曲线相交的地方就会产生分岔。 分岔是动力系统中一种常见的现象,会出现稳定性变化或/和产生新的轨道族分支。 本文主要考虑了切分岔、倍周期分岔、二次Hopf 分岔与修正二次Hopf 分岔,如表1所示[25-28]。

图2 稳定性图[26]Fig.2 Stability diagram[26]

表1 分岔类型[25-28]Table 1 Bifurcation type[25-28]

3 DRO 轨道族的分岔及延拓

3.1 DRO 轨道族的稳定性与分岔

研究的DRO 轨道族的能量范围为2≤J≤3.2,涵盖了地月之间大部分区域,轨道形状如图3 所示。 在这个能量范围内绘制DRO 轨道族的稳定性指数随轨道能量的变化,如图4 所示。

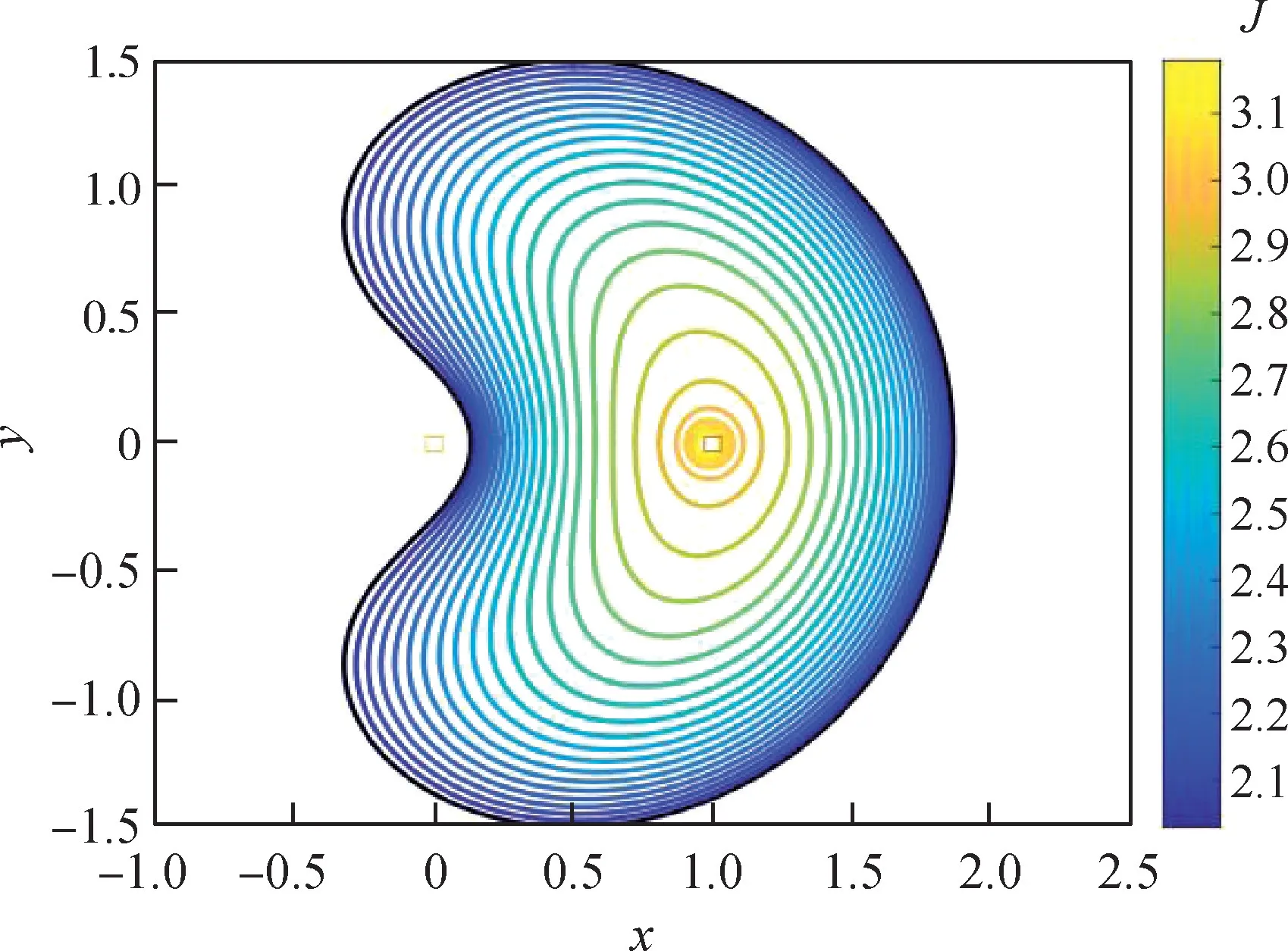
图3 地月空间DROFig.3 DRO in Earth-Moon system

图4 DRO 稳定性指数Fig.4 Stability indices of DRO

观察可知,当2.365≤J≤3.2 时,所有稳定性指数vi=1,表示该范围的DRO 轨道均线性稳定。而当J＜2.365 时,稳定性指数开始偏离,并始终略大于1,此时对应的平面DRO 轨道略不稳定。

为了更深入理解DRO 轨道族的特征结构演化,在Broucke 稳定性图上绘制了其特征参数α和β的变化,如图5 所示。

图5 DRO 轨道族的Broucke 稳定性图Fig.5 Broucke stability diagram of DRO family

观察可知,DRO 轨道族主要发生的分岔类型为切分岔和倍周期分岔。 分岔方程分别使用不同颜色的虚线标注,DRO 在与分岔方程的相交点处发生分岔,用与分岔方程相同颜色的“*”标记,此时产生对应分岔类型的轨道族。 可以看到,J＞2.355 时的交叉点均发生倍周期分岔;而在J＜2.355时,DRO 轨道族的稳定性曲线与切分岔轨迹线相交并过渡到不稳定区域,平面DRO 不再稳定。 这时产生了新的轨道族,即三维的DRO。

分岔到三维的DRO 分支的几何特征如图6 所示。 三维DRO 轨道族均具有z向的振幅,其中某些轨道能够避开月球的遮挡,与地球进行连续通信。

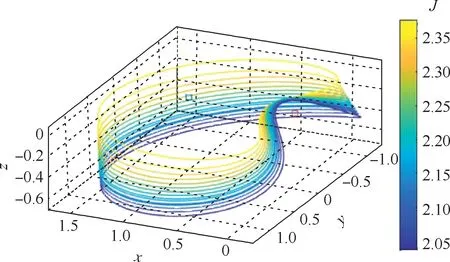
图6 三维DROFig.6 3D DRO

三维DRO 轨道族分支的稳定性指数如图7所示。 所有稳定性指数vi=1,轨道均线性稳定。这是因为在发生切分岔时,单值矩阵的2 个非平凡特征值趋于统一,此时λ1=1/λ1= +1,轨道稳定性从平面DRO 过渡到了三维DRO 分支上[29-30]。

图7 三维DRO 的稳定性指数Fig.7 Stability indices of 3D DRO

3.2 DRO 周边多周期轨道族的延拓与稳定性

在J＞2.355 的稳定区域内,从Broucke 图的分岔点处向外延拓求解其余周期轨道分支,得到如下一系列多周期轨道族。

1) 三周期平面DRO

在Broucke 图上,DRO 与3 倍周期分岔方程(见图5 中深蓝色虚线)分别在J= 2. 85、J=2.955两处相交。 三周期平面DRO(P3DRO)在整个2 ≤J≤3. 2 范围内都存在,均为平面轨道。图8为P3DRO 的延拓结果。

图8 P3DROFig.8 P3DRO

图9 分别展示了该轨道族在不同延拓阶段下的几何形状,对应了不同的轨道能量。 可见,随着J的数值从2 开始逐渐增大,P3DRO 的轮廓逐渐变小缩窄,轨道之间的间隔也不断缩小;直到J=2. 85 处,P3DRO 与DRO 重合。 当J开始偏离2.85时,P3DRO 立即与DRO 分离。 随着J的增大,一开始其内侧轨道相对外侧轨道的缩小速度更大,随后外侧轨道相对缩小速度加快,最终在J=2.955 处P3DRO 再次与DRO 重合。 当J偏离2.955 后P3DRO 又分离演变成另一种形状。 可以看出,同一轨道分支在发生分岔前后的几何形状差异很大,可以根据几何形状应用于多种任务场景。

图9 P3DRO 的几何特性Fig.9 Geometric properties of P3DRO

图10 展示了P3DRO 的稳定性指数。 可以发现,除2 处分岔点之外,其余轨道均有vi＞1,轨道均非常不稳定。

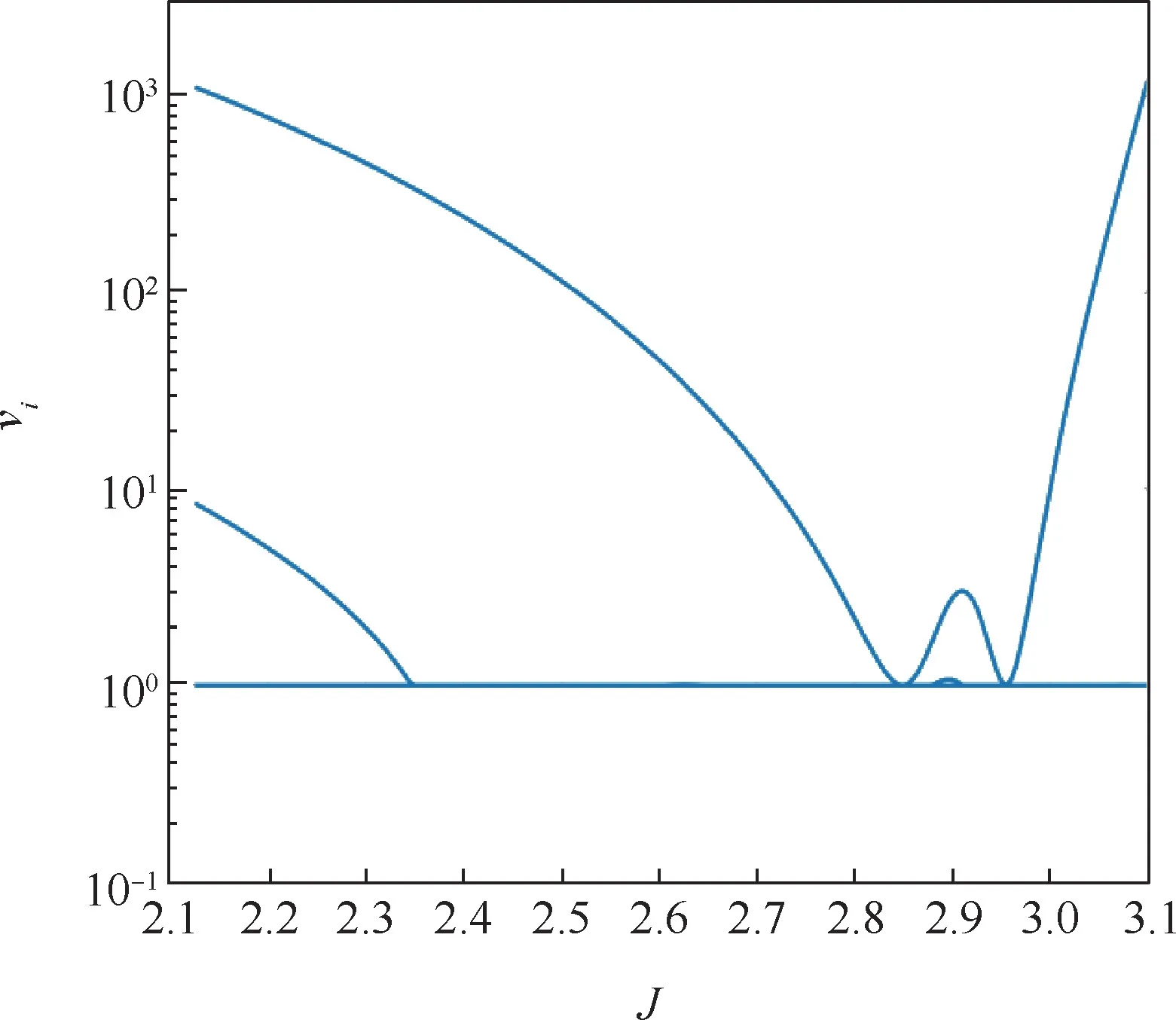
图10 P3DRO 的稳定性指数Fig.10 Stability indices of P3DRO

2) 四周期平面DRO

在Broucke 图上,DRO 与4 倍周期分岔方程(见图5 中红色虚线)分别在J=2.72、J=2.995两处相交,沿J≤2. 72 及J≥2. 995 方向延拓出2 个平面分支。 图11 和图12 显示了四周期平面DRO(P4DRO)2 个分支的延拓结果。

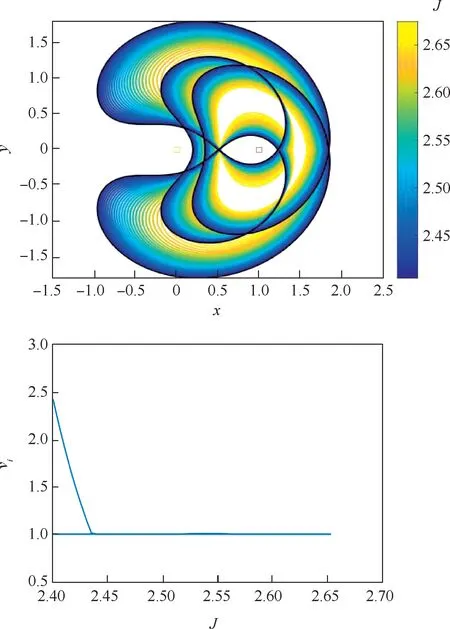
图11 P4DRO 分支1 的延拓及其稳定性指数Fig.11 Stability indices of P4DRO-1

图12 P4DRO 分支2 的延拓及其稳定性指数Fig.12 Stability indices of P4DRO-2

可以看出,P4DRO 的前一个分支在J≥2.43的范围内线性稳定,而后一个分支均不稳定。

3) 五周期平面与三维DRO

在Broucke 图上,DRO 与5 倍周期分岔方程(见图5 中黑色虚线)分别在J=2. 45、J=2. 9、J=2.99、J=3.025 四处相交,发生了4 次分岔。其中,在J≤2.45、J≥3.025 两处延拓出2 个平面分支,而在J≤2.9、J≥2.99 两处延拓出2 个三维分支。 图13 和图14 展示了五周期平面与三维DRO(P5DRO)的2 个平面分支。 图15 和图16 则展示了三维P5DRO。

图13 P5DRO 平面分支1 的延拓及其稳定性指数Fig.13 Stability indices of 2D-P5DRO-1

图14 P5DRO 平面分支2 的延拓及其稳定性指数Fig.14 Stability indices of 2D-P5DRO-2

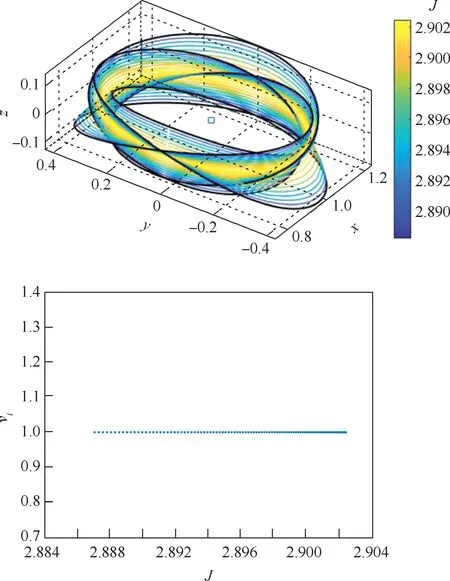
图15 P5DRO 三维分支1 的延拓及其稳定性指数Fig.15 Stability indices of P5DRO-3D-1

图16 P5DRO 三维分支2 的延拓及其稳定性指数Fig.16 Stability indices of P5DRO-3D-2

P5DRO 的2 个平面分支均不稳定。 对三维分支而言,能量在J=2.9 附近的P5DRO 分支均线性稳定,而后一个三维P5DRO 分支在J＞2.996处开始则表现不稳定。 仔细观察可以发现,P5DRO 存在同一能量对应超过3 个稳定性指数的现象,这是因为在P5DRO 的分支中,可能存在同一能量下对应多个轨道的情况,如图17 所示。此时需要根据延拓情况更改延拓参数的选择。

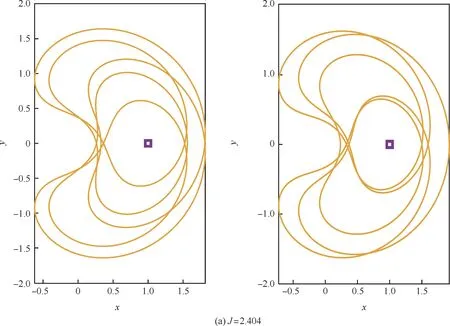
图17 同一能量对应多个P5DROFig.17 Different P5DRO with same Jacobi energy

3.3 多周期轨道族的流形

对于3.2 节得到的轨道分支,可以看到不同轨道分支的最大稳定性指数范围各异,除了P3DRO 的最大稳定性指数涵盖了[100,103]区间范围以外,其余轨道分支稳定性指数大都有vmax＜10。 为了更直观理解稳定性指数大小对轨道流形的影响,分别选取了最大稳定性指数为12.319 9、22.711 7、61.241 4、129.665 6 的多个P3DRO 进行对比,绘制2 个轨道周期时间内的稳定流形,如图18 所示;以及最大稳定性指数为6.634 4 的三维P5DRO 在3 个周期时间内的轨道稳定流形,如图19 所示。 其中,黄色和绿色分别表示稳定流形沿正负方向的2 个分支。 观察可知,当最大稳定性指数vmax＜10 时,其轨道流形并不明显。 在之前各周期轨道的延拓分支中,三维DRO 及三维P5DRO 的其中一个分支均线性稳定,其余轨道分支稳定性指数大都处于近似稳定或略微不稳定的状态。 因此在设计转移轨道时,可主要利用P3DRO 周围的流形。

图18 不同稳定性指数下的稳定流形Fig.18 Manifold in different stability indices

图19 不同稳定性指数下的稳定流形(J =3.003 5,vmax =6.634 4)Fig.19 Manifold in different stability indices(J =3.003 5,vmax =6.634 4)

为了在设计转移轨道时能更方便地利用流形,选取了vmax=55.495 2 的二维P3DRO 和vmax=6.634 4 的三维P5DRO,在庞加莱截面分别绘制了稳定流形穿越的坐标,如图20 和图21 所示。对平面轨道,选取y=0 作为截面,绘图坐标分别为x和vx;对于三维轨道,选取x=1 -μ作为截面,绘图坐标分别考虑为y-z-vx和y-z-vy。 其中,蓝色和灰色分别表示积分3、12 个轨道周期内的流形映射在截面上的点,红色点表示周期轨道本身。从这些区域的点中读取状态信息,可选取合适的值进行转移轨道的设计。

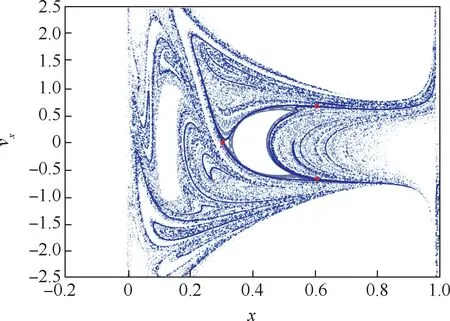
图20 y =0 截面处二维P3DRO 的稳定流形(J =2.58,vmax =55.495 2)Fig.20 Manifold section of 2D P3DRO in y =0 section(J =2.58,vmax =55.495 2)

图21 x =1 -μ 截面处三维P5DRO 的稳定流形(J =3.003 5,vmax =6.634 4)Fig.21 Manifold section of 3D P5DRO in x =1 -μ section(J =3.003 5,vmax =6.634 4)

3.4 分岔结构与轨道周期

将DRO 轨道族发生分岔后的延拓结果绘制成如图22 所示的能量-状态(J-x-vy)关系图,可以更清晰地展示DRO 轨道族的分岔结构。

图22 分岔图Fig.22 Bifurcation chart

定义N-周期DRO 的平均周期为T/N,T为轨道完整重复一次的轨道周期。 图23 绘制了不同周期轨道族的能量与平均周期关系,图24为放大显示的P5DRO 四个分支的能量与平均周期关系。

图23 能量-周期关系Fig.23 Relationship between energy and period

由图23 可知,不同周期轨道的平均周期T/N均随J的增加而单调下降。 其中,分岔到三维的DRO 分支与平面DRO 的平均周期相同。 P3DRO 的 中 间 分 支, 即 在2. 85 ≤J≤2.955 处, 其 平 均 周 期 与 DRO 相 同。 三 维P5 DRO 与平面P5DRO 的能量-周期关系放大后如图24 所示,存在同一能量对应多个轨道周期的情况。 二维平面的倍周期分岔轨道的平均周期均在P3 DRO 与DRO 的周期范围之间。 研究周期轨道族的平均周期T/N,可以为一些空间任务提供选择初始参数的参考依据,如对在DRO 的多个轨道族上进行卫星编队进行周期匹配等。

图24 P5DRO 的能量-周期关系放大图Fig.24 Relationship between energy and period of P5DRO and its local magnification

4 结 论

1) DRO 轨道族主要发生切分岔和倍周期分岔,其中切分岔会改变轨道稳定性,倍周期分岔的稳定性则不变。 分岔后的不同分支之间几何形状差异大。

2) P3DRO 的稳定性指数范围最大,流形结构明显,其余轨道分支则线性稳定或近似稳定。

3) DRO 轨道族的平均周期T/N随着能量值J升高而单调下降。 其中分岔到三维的DRO 分支与平面DRO 的周期相同,P5DRO 存在同一能量对应多个轨道周期的情况,平面倍周期分岔轨道的平均周期介于DRO 与P3DRO 之间。