凸域上拟双曲测地线直径的Gehring-Hayman恒等式

钱伟茂,张益池

(1.湖州广播电视大学远程教育学院,浙江湖州 313000; 2.湖州职业技术学院机电工程学院,浙江湖州 313000)

凸域上拟双曲测地线直径的Gehring-Hayman恒等式

钱伟茂1,张益池2

(1.湖州广播电视大学远程教育学院,浙江湖州 313000; 2.湖州职业技术学院机电工程学院,浙江湖州 313000)

将平面Jordan域上关于双曲测地线直径的Gehring-Hayman不等式推广到n维空间凸域上的拟双曲测地线.利用M¨obius变换和拟双曲度量证明了n维空间凸域上连接任意二点x和y的拟双曲测地线的直径等于x与y之间的Euclidean距离.所得结果推广和改进了相关已有结果.

凸域;拟双曲长度：拟双曲距离;拟双曲测地线;Gehring-Hayman不等式

1 引言

其中(1)式中的下确界是对D中全体连结x,y二点的可求长曲线γ所取,f(z)为D到单位圆B2(0,1)上的任一共形映射.称(1)式中达到下确界的曲线γ为D中连结x与y二点的双曲测地线.

1962年,文献[2]得到:

定理1.1[2]设D是R2中的Jordan域,x,y∈D是任意二点,γ是D中连结x与y二点的双曲测地线.若α是D中连结x与y二点的任意可求长曲线,则

其中4.5≤c1≤17.5是一绝对常数.

称不等式(2)为双曲测地线长度的Gehring-Hayman不等式.

1998年,文献[3]得到:

定理1.2[3]设D是R2中的Jordan域,x,y∈D是任意二点,γ是D中连结x与y二点的双曲测地线.若α是D中连结x与y二点的任意可求长曲线,则

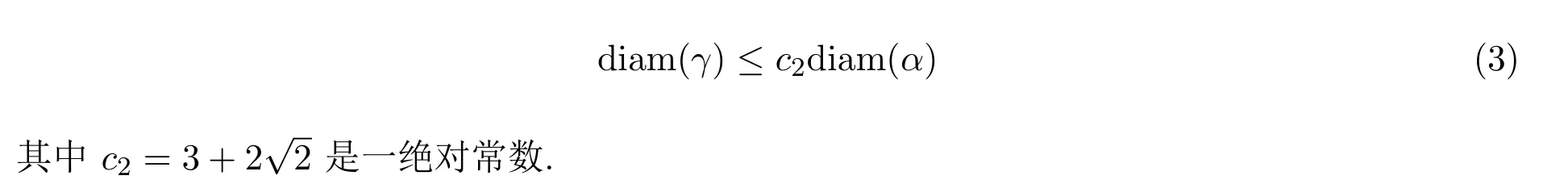
称不等式(3)为双曲测地线直径的Gehring-Hayman不等式.

上述不等式(2)或(3)在平面拟共形映射[4-6]、共形几何[7-10]、John圆几何[11]、Gromov双曲性[12]及调和测度[13-14]等理论中均有广泛的应用.

由于Riemann映射定理在高维空间的一般Jordan域上已不再成立,因此在高维空间的一般Jordan域上就不能类似于平面一样来定义双曲距离.为此Gehring和Palka在文献[15]中定义了空间区域上的拟双曲度量.其定义如下:

设D是Rn中的区域,x1,x2∈D,γ是D中连结x1与x2二点的任一可求长曲线,称

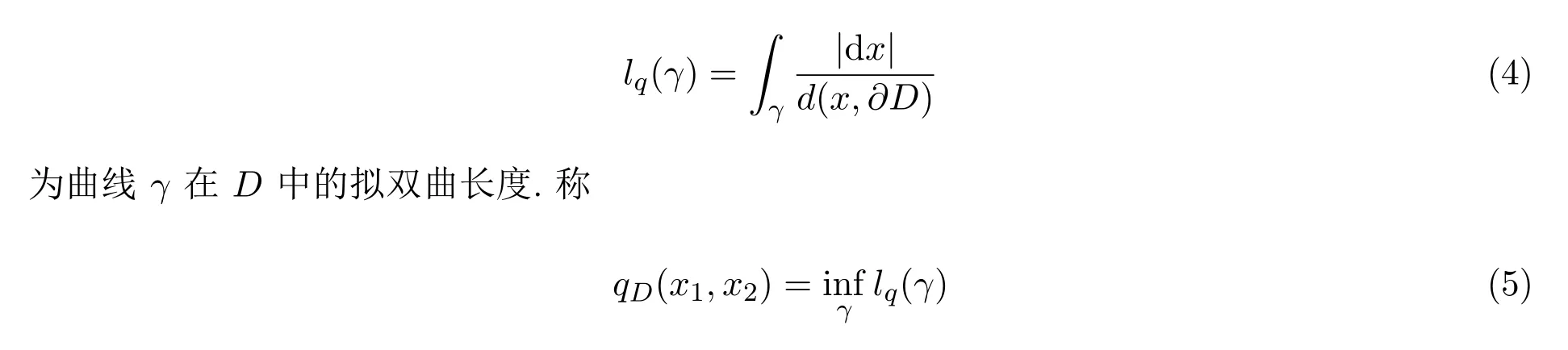
为x1,x2在D中的拟双曲距离,其中(5)中的下确界是对D中全体连结x1,x2二点的可求长曲线γ所取.称(5)中达到下确界的可求长曲线β为D中连结x1与x2二点的拟双曲测地线.

1999年文献[16]中证明了Rn中的任意区域上连结任意二点的拟双曲测地线存在且唯一.拟双曲测地线和拟双曲距离有着双曲测地线和双曲距离许多类似的几何与分析性质.特别是拟双曲测地线和拟双曲测距离在高维拟共形映射[17-19]和John域[20-21]等理论中恰好发挥着双曲测地线和双曲距离在平面相应理论研究中的作用.

1994年文献[22]证明了当n=2时,不等式(3)对单连通区域D上的拟双曲测地线是成立的;当n≥3时,若D可以拟共形映射到单位球,则不等式(3)对区域D上的拟双曲测地线也是成立的.Pommerenke和Rohde在文献[3]中猜测不等式(3)对Rn中单连通区域D上的拟双曲测地线成立.本文的目的是证明当D是Rn中的凸域时,上述Pommerenke和Rohde猜想成立,即证明下面凸域上拟双曲测地线的Gehring-Hayman恒等式.

定理设D是Rn中的凸域,x,y是D中任意二点.若γ是D中连结x,y二点的拟双曲测地线,则diam(γ)=|x-y|.

2 引理

为了定理证明过程中叙述的方便,在定理证明之前首先建立下列四则引理.

引理2.1[23]设D⊆Rn是一凸域,则对任意x,y∈D和0≤α,β≤1,α+β=1,恒有

3 定理的证明

参考文献

[2]Gehring F W,Hayman W K.An Inequality in the theory of conformal mapping[J].J.Math.Pure Appl., 1962,41:353-361.

[3]Pommerenke Ch,Rohde S.The Gehring-Hayman inequality in conformal mapping[C]//Gehring F W, Duren P L.Quasiconformal Mapping and Analysis.New York:Springer Verlag,1998.

[4]Heinonen J.The diameter conjecture for quasiconformal maps is true in space[J].Proc.Amer.Math.Soc., 1995,123(6):1709-1718.

[5]Martio O,Nakki R.Boundary H¨older continuity and quasiconformal mappings[J].J.London Math.Soc., 1991,44(2):339-350.

[6]Jaenisch S.Length distortion of curves under conformal mappings[J].Michigan Math.J.,1968,15:121-128.

[7]Oyma K.Harmonic measure and conformal length[J].Proc.Amer.Math.Soc.,1992,115(3):687-689.

[8]Fern´andez J L,Hamilton D H.Length of curves under conformal mappings[J].Comment.Math.Helv., 1987,62(1):122-134.

[9]Gehring F W,Hayman W K,Hinkkanen A.Analytic functions satisfying H¨older conditions on the boundary[J].J.Approx.Theory,1982,35(3):243-249.

[10]Kaufman R,Wu J M.Distances and the Hardy-Littlewood property[J].Complex Variables Theory Appl., 1984,4(1):1-5.

[11]Kim K.Harmonic measure and hyperbolic distance in John disks[J].Math.Scand.,1998,83(2):283-299.

[12]Balogh Z M,Buckley S M.Geometric characterizations of gromov hyperbolicity[J].Invent.Math.,2003, 153(2):261-301.

[13]Bishop C J,Jones P W.Harmonic measure and arclength[J].Ann.Math.,1990,132(3):511-547.

[14]Llorente J G.On the Gehring-Hayman property,the Privalov-Riesz theorems,and doubling measures[J], Michigan Math.J.,2004,52(3):553-571.

[15]Gehring F W,Palka B P.Quasiconformally homogeneous domains[J].J.Analyse Math.,1976,30:172-199.

[16]Gehring F W,Osgood B G.Uniform domains and the quasi-hyperbolic metric[J].J.Analyse Math., 1979,36:50-74.

[17]Herron D A,Koskela P.Conformal capacity and the quasihyperbolic metric[J].Indiana Univ.Math.J., 1996,45(2):333-359.

[18]Martin G J.Quasiconformal and bi-Lipshitz homeomorphisms uniform domains and the quasihyperbolic metric[J].Trans.Amer.Math.Soc.,1985,92(1):169-191.

[19]Martin G J,Osgood B G.The quasihyperbolic metric and associated estimates on the hyperbolic metric [J].J Analyse Math.,1986,47:37-53.

[20]Herron D A.John domains and the quasihyperbolic metric[J].Complex Variables Theory Appl.,1999,39(4): 327-334.

[21]Gehring F W,Hag K,Martio O.Quasihyperbolic geodesics in John domains[J].Math.Scand.,1989,65(1): 75-92.

[22]Heinonen J,Nakki R.Quasiconformal distortion on arcs[J].J.Anal.Math.,1994,63:19-53.

The Gehring-Hayman identity for the diameter of quasihyperbolic geodesics in convex domain

Qian Weimao1,Zhang Yichi2
(1.School of Distance Education,Huzhou Broadcast and TV University,Huzhou313000,China;
2.School of Mechanical and Electrical Engineering,Huzhou Vocational and Techincal College, Huzhou313000,China)

Generalize the Gehring-Hayman inequality for the diameter of the hyperbolic geodesics in the plane Jordan domain to the quasihyperbolic geodesics in the convex domain of n-dimensional space.Making use of the M¨obius transformation and the quasihyperbolic metric,we prove that the diameter of the quasihyperbolic geodesics with the endpoints x and y in the convex domain of n-dimensional space is equal to the Euclidean distance between x and y.The obtained result is a generalization and improvement of some known results.

convex domain,quasihyperbolic length,quasihyperbolic distance,quasihyperbolic geodesics, Gehring-Hayman inequality

O174.55

A

1008-5513(2013)03-0241-05

10.3969/j.issn.1008-5513.2013.03.004

2012-08-13.

浙江省自然科学基金(LY13A010004);国家开放大学基金(Q1601E-Y);浙江省教育厅基金(Y201223519).

钱伟茂(1962-),副教授,研究方向:复分析.

2010 MSC:30F45