极小素子模及其拓扑性质
张国印
(金陵科技学院公共基础课部,江苏 南京 211169)
本文假定所涉及到的环都是带单位元的结合环,模都是酉模。一个环R的左纯理想(理想)P被称为是素左理想[1](素理想),如果a,b∈R且aRb⊆P,则a∈P或b∈P。设M是左R-模,M的左零化子记作M⊥={r∈R|rM=0},因此(M/N)⊥={r∈R|rM⊆N},其中N是M的子模。本文用Spec(R)、Max(R)分别表示R的所有素理想的集合、所有极大理想的集合。
设M是左R-模且K是M的纯子模,如果满足rRm⊆K,m∈M,r∈R,则r∈(M/K)⊥或m∈K,则称K是M的素子模[2]。M的极大子模是素子模。显然,环R的素左理想、素理想都是R作为左模RR的素子模。用Specl(M)、Maxl(M)、Minspecl(M)分别表示左R-模M的所有素子模的集合、所有极大子模的集合、所有极小素子模的集合。设R是任意环,M是左R-模,如果对任意M的子模N,都存在R的理想I,使得N=IM,则称M是左乘法R-模[3]。关于乘法模的研究见文献[4-6]。本文证明(见命题1.5):如果M是左乘法R-模,对任意Q∈Max(R)且Q⊇M⊥,都有QM≠M,则:M一定存在极大子模和极小素子模,且极大子模可表示为:Max(M)={QM|Q∈Max(R),Q⊇M⊥};进一步若M是交换环R上的乘法模,则极小素子模与极小素理想的关系为:Minspec(M)={PM|P⊇M⊥,(P/M⊥)∈Minspec(R/M⊥)},且其所有素子模可表示为:Specl(M)={PM|P∈Spec(R),P⊇M⊥}。
设M是左R-模,N是M的子模,Ul(N)表示所有不包含N的M的素子模的集合,且Vl(N)=Specl(M)Ul(N)。显然Ul(0)=Ø,Ul(M)=Specl(M),文献[2]给出了如下定义:对左R-模M,如果对任意M的子模L1,L2,都存在M的子模N,使得Ul(L1)∩Ul(L2)=Ul(N),则称M是拓扑模。关于拓扑模的研究见文献[2,7-8]。
称作f:X→Y是保核收缩映射(其中X是拓扑空间且Y⊂X),如果f是连续映射,且f|Y是恒等映射,也称作Y是X的保核收缩(Retraction)。Demarco与Orsatti在文献[9]中表明如果R是交换环R,则Spec(R)是正规的拓扑空间的充分必要条件是Max(R)是Spec(R)的保核收缩。本文将此结果推广到非交换环上的左拓扑R-模M上(见定理2.3):如果左R-模M是有限生成的拓扑模,则Maxl(M)∪Minspecl(M)是正规的拓扑空间的充分必要条件是Maxl(M)是Maxl(M)∪Minspecl(M)的保核收缩且Maxl(M)是Hausdorff空间。关于环、模的一系列拓扑性质的研究见文献[1,2,5,7-12]。
1 极小素子模
引理1.1对任意环R,M是左R-模且Specl(M)≠Ø,则任意M的素子模都包含有极小素子模。

命题1.2如果R是环且M是有限生成的左R-模,则M一定存在极小素子模。
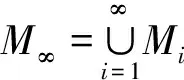
R是环,M是左R-模,N是M的子模,定义(M/N)⊥为子模N的左乘理想,记作Il(N),即Il(N)=(M/N)⊥。特别是对M的任意元素m,Rm的左乘理想简称为元素m的左乘理想,记作Il(m),即Il(m)=Il(Rm)=(M/Rm)⊥。如果M是左乘法R-模,对M的子模N,一定有N=(M/N)⊥M=Il(N)M。理由如下:M的子模N,一定有R的理想I,使得N=IM,显然I⊆(M/N)⊥,因此N=IM⊆(M/N)⊥M⊆N。环R称作左quasi-duo环[13]如果每一个左极大理想是双边理想。
命题1.3如果R是左quasi-duo环,M是非零的左乘法R-模,且对R的任意极大理想Q和M的任意元素m的左乘理想Il(m)满足QIi(m)=Ii(m)Q,则它一定存在极小素子模。
证明下边只要证明非零乘法左R-模M一定包含一个极大子模,而极大子模一定是素子模,然后Specl(M)≠Ø,根据引理1.1,该命题即可证明。
设N是非零左乘法R-模M的一个纯子模,则M/N也是非零左乘法R-模。设m∈M且m≠0,则l(m)={a∈R|am=0}是一个纯左理想,因此l(m)一定包含在某极大左理想Q中。又因R是左quasi-duo环,因此Q是极大理想。因M是左乘法R-模,故对m的左乘理想I=Il(m),一定有Rm=IM。反设M=QM,由命题条件知Rm=IM=I(QM)=Q(IM)=QRm=Qm,因此存在元素b∈Q,使得m=bm,即(1-b)m=0,因此1-b∈l(m)⊆Q,显然b,1-b不能同时属于极大理想Q中,这是矛盾的。因此M≠QM。下证明QM是M的极大子模。假设存在M的一个子模N满足QM⊆N⊆M且N≠M,由M是乘法模条件知,则一定存在R的理想J,使得N=JM,记作(M/N)⊥=P,显然J⊆P,N=JM⊆PM⊆N,因此JM=PM=N。又因且QM⊆N⊆M,则Q⊆(M/N)⊥=P,因此Q=P,进而N=QM,因此QM是M的极大子模。 证毕。
由命题1.3直接可得,交换环上乘法模一定存在极小子模。关于交换环上乘法模的研究见文献[5-6]。
推论1.4如果R是交换环,且M是非零乘法R-模,则它一定存在极小素子模。
如果R是环且M是左R-模,如果存在Q∈Max(R)且Q⊇M⊥,有QM≠M,则(M/QM)⊥=Q,由文献[13]引理1.3知,QM一定是素子模,即有Specl(M)≠Ø,进而由引理1.1知,Minspecl(M)≠Ø。
命题1.5如果R是环且M是左乘法R-模,对任意Q∈Max(R)且Q⊇M⊥,都有QM≠M,则:
1)M一定存在极大子模,且Max(M)={QM|Q∈Max(R),Q⊇M⊥};
2)M一定存在极小素子模;
3) 如果R是交换环,则Spec(M)={PM|P∈Spec(R),P⊇M⊥};
4) 如果R是交换环,则有:
Minspec(M)={PM|P⊇M⊥,(P/M⊥)∈Minspec(R/M⊥)}。


前边已证明M存在极大左R-子模,对任意H∈Maxl(M)≠Ø,由于M是左乘法R-模,记(M/H)⊥=Q⊇M⊥,则H=QM。如果Q⊆Q1且Q1∈Max(R),则H=QM⊆Q1M≠M,因此H=QM=Q1M,因而Q1⊆(M/H)⊥=Q,因此Q=Q1,有Maxl(M)⊆{QM|Q∈Max(R),Q⊇M⊥}。反过来对任意Q∈Max(R),且Q⊇M⊥,下证明QM(≠M)是左极大子模。若存在H∈Maxl(M)使得QM⊆H,令Q1=(M/H)⊥⊇M⊥,则Q1≠R,Q⊆Q1,因此Q=Q1,进而有QM=Q1M=H∈Maxl(M),即{QM|Q∈Max(R),Q⊇M⊥}⊆Maxl(M)。综合上述有Maxl(M)={QM|Q∈Max(R),Q⊇M⊥}。
2) 以上1)中已经证明M一定存在极大左R-子模,而每一个极大左R-子模都是左素子模,因此Specl(M)≠Ø,然后根据引理1.1知它一定存在极小素子模。
3) 如果R是交换环,由文献[6]的推论2.11知,R-模M的一个纯的子模N是素子模,当且仅当(M/N)⊥是素理想,当且仅当存在R的素理想P⊇M⊥,使得N=PM。⟹):如果N是R-模M的素子模,则(M/N)⊥=P是R的素理想且N=PM≠M。⟸):任意P∈Spec(R),P⊇M⊥,则存在极大子模Q⊇P,使得M⊇QM⊇PM,且M≠QM,因此,由文献[6]的推论2.11知,PM是R-模M的一个纯的子模,因此PM是M的素子模。
4) 文献[6]中有结果:N是极小素子模的充分必要条件是存在素理想P⊇M⊥且(P/M⊥)∈Minspec(R/M⊥),使得N=PM≠M,因此Minspec(M)⊆{PM|P⊇M⊥,(P/M⊥)∈Minspec(R/M⊥)};反过来,任取P⊇M⊥,(P/M⊥)∈Minspec(R/M⊥),则存在极大子模Q⊇P,使得M⊇QM⊇PM,且M≠QM,故PM是R-模M的一个纯的子模,进而有:{PM|P⊇M⊥,(P/M⊥)∈Minspec(R/M⊥)}⊆Minspec(M)。证毕。
Lu(1995,定理6)[14]表明:如果R是交换环且M是有限生成的乘法R-模,则映射ψ:Spec(M)→Spec(R/M⊥)是一一映射,且对任意K∈Spec(M),ψ(K)=(M/K)⊥/M⊥,因此对任意Q∈Max(R)且Q⊇M⊥,都有唯一的素子模K,使得(M/K)⊥=Q,因而由K=QM是素子模知QM≠M。从而直接由命题1.5可得两个限制映射:
ψ|Max(M):Max(M)→Max(R/M⊥)与ψ|Minspec(M):Minspec(M)→Minspec(R/M⊥)也是一一映射,且有如下结果。
推论1.6如果R是交换环且M是有限生成的乘法R-模,则有1) 对任意Q∈Max(R)且Q⊇M⊥,都有QM≠M;2)Max(M)={QM|Q∈Max(R),Q⊇M⊥};3)Spec(M)={PM|P∈Spec(R),P⊇M⊥};4)Minspec(M)={PM|P⊇M⊥,(P/M⊥)∈Minspec(R/M⊥)}。
2 极小素谱的拓扑性质
称作左R-模M是pm模[2,5],如果M的任意纯子模都包含在一个极大子模之中,且M的任意素子模都包含在唯一的一个极大子模之中。
命题2.1如果左R-模M的任意纯子模都包含在一个极大子模之中,则M是pm模当且仅当M的任意极小素子模都包含在唯一的一个极大子模之中。
证明:⟹):显然。⟸):如果左R-模M的任意纯子模都包含在一个极大子模之中,则Specl(M)≠Ø。任取K∈Specl(M),由引理1.1知,每一个素子模都包含一个极小素子模,不妨设K0∈Minspecl(M),使得K⊇K0,又因K0包含在唯一的一个极大子模之中,从而K必包含在唯一的一个极大子模之中。 证毕。
命题2.2如果左R-模M是拓扑模,M的任意纯子模都包含在一个极大子模之中,且Maxl(M)是Maxl(M)∪Minspecl(M)的保核收缩,则M是pm模。

定理2.3如果R是任意带单位元的结合环,左R-模M是有限生成的拓扑模,则Maxl(M)∪Minspecl(M)是正规的拓扑空间的充分必要条件是Maxl(M)是Maxl(M)∪Minspecl(M)的保核收缩且Maxl(M)是Hausdorff空间。
证明由于R-模M是有限生成的,由命题1.2知,M的极大子模与极小子模都存在。由于左R-模M是拓扑模,故Specl(M)上定义了Zariski拓扑,因而Maxl(M),Minspecl(M),Maxl(M)∪Minspecl(M)上都有相应的诱导拓扑或相对拓扑。根据文献[8]知,Maxl(M)是紧致的拓扑空间。
⟹):如果Maxl(M)∪Minspecl(M)是正规的拓扑空间,任取两个不相等的极大理想H1,H2,{H1},{H2}是两个不相等闭集,存在两个互不相交的Maxl(M)的开集,分别包含{H1},{H2},故Maxl(M)是Hausdorff空间。
对M的子模N1,N2,容易验证如下三条件等价:1)N1+N2=M;2)Vl(N1)∩Vl(N2)∩[Maxl(M)∪Minspecl(M)]=Ø;3)Vl(N1)∩[Maxl(M)∪Minspecl(M)]⊆Ul(N2)∩[Maxl(M)∪Minspecl(M)]。
Maxl(M)∪Minspecl(M)是正规的拓扑空间,即:如果两不相交闭集Vl(N1)∩Vl(N2)∩[Maxl(M)∪Minspecl(M)]=Ø,一定存在两个不相交的开集Ul(L1)∩Ul(L2)∩[Maxl(M)∪Minspecl(M)]=Ø,使得Vl(Ni)∩[Maxl(M)∪Minspecl(M)]⊆Ul(Li)∩[Maxl(M)∪Minspecl(M)],i=1,2。因此,Maxl(M)∪Minspecl(M)是正规的拓扑空间,当且仅当,对左R-模M的子模N1,N2,如果N1+N2=M,则一定存在M的子模L1,L2,使得Ni+Li=M,i=1,2,且Ul(L1)∩Ul(L2)∩[Maxl(M)∪Minspecl(M)]=Ø。
对K∈Maxl(M)∪Minspecl(M),定义集合AK表示所有满足N+K=M的M的子模N的集合,则AK有如下性质(1)如果N1∈AK且N1⊆N2,则N2∈AK;性质(2)如果N1+N2∈AK,则N1∈AK或者N2∈AK;这是因为N1+N2∈AK,即(N1+N2)+K=M=N1+(N2+K),由于Maxl(M)∪Minspecl(M)是正规的拓扑空间,则一定存在M的子模L1,L2,使得N1+L1=M,(N2+K)+L2=M且Ul(L1)∩Ul(L2)∩[Maxl(M)∪Minspecl(M)]=Ø,若H∈Maxl(M)∪Minspecl(M),则H⊇L1或H⊇L2。因此对于上边的K,K⊇L1或者K⊇L2,进而N1+K=M或(N2+K)+K=N2+K=M,所以N1∈AK或者N2∈AK。

⟸):如果映射f:Maxl(M)∪Minspecl(M)→Maxl(M)是保核收缩映射,由命题2.2知,M是pm左R-模,对任意K∈Maxl(M)∪Minspecl(M),f(K)=H∈Maxl(M),H是唯一包含K的M的极大子模(看命题2.2的证明过程知)。对任意闭集Vl(N)∩[Maxl(M)∪Minspecl(M)],其中N是R-模M的子模,则有f{Vl(N)∩[Maxl(M)∪Minspecl(M)]}=Vl(N)∩Maxl(M)。如果B1,B2是Maxl(M)∪Minspecl(M)的两个闭集且B1∩B2=Ø,由于Maxl(M)是紧致的Hausdorff空间,由文献[15]的定理5.9知,Maxl(M)是正规的,因此对不相交的两个闭集B1∩Maxl(M),B2∩Maxl(M),必存在不相交的两个开集U1,U2,使得B1∩Maxl(M)⊆U1,B2∩Maxl(M)⊆U2,因此f-1(U1),f-1(U2)是两个不相交的开集且B1⊆f-1(U1),B2⊆f-1(U2),因此Maxl(M)∪Minspecl(M)是正规的拓扑空间。 证毕。
左乘法R-模一定是拓扑模,见文献[3],因此直接可得如下结论。
推论2.4如果左R-模M是有限生成的乘法模,则Maxl(M)∪Minspecl(M)是正规的充分必要条件是Maxl(M)是Maxl(M)∪Minspecl(M)的保核收缩且Maxl(M)是Hausdorff空间。
3 结 语
对于存在素子模的左R-模M,尽管Maxl(M)∪Minspecl(M)⊆Specl(M),但∩{K∈Maxl(M)∪Minspecl(M)}=∩{K∈Specl(M)}都等于模M的素根,因此对拓扑模或乘法模上拓扑空间Maxl(M)∪Minspecl(M)与Specl(M)的拓扑性质(如正规性、连通性、谱空间性等)的比较研究,及其这些拓扑性质与模的性质的关系等,都有待进一步研究。
[1] ZHANG Guo-yin,TONG Wen-ting,WANG Fang-gui.Spectrum of a Noncommutative Ring[J].Comm Algebra,2006,34(8):2795-2810
[2] 张国印.拓扑模的谱[J].金陵科技学院学报,2006,22(3):5-8
[3] ZHANG Guo-yin.Multiplication Modules over any Rings[J].J of Nanjing Univ.Math Biquarterly,2006,23(1):59-69
[4] Tuganbaev A A.Multiplication Modules over Non-communicative Rings[J].Sbornik:Mathematics,2003,194(12):1837-1864
[5] ZHANG Guo-yin,WANG Fang-gui,TONG Wen-ting.Multiplication Modules in which Every Prime Submodule is Contaied in a Unique Maximal Submodule[J].Comm Algebra,2004,32(5):1945-1959
[6] Abd El-Bast,Z,Smith,P F. Multiplication Modules[J].Comm Algebra,1988,16(4):32-36
[7]张国印.单列模与拓扑模[J].金陵科技学院学报,2006,22(2):1-4
[8] Zhang Guo-yin,Tong Wen-ting.Spectral Spaces of Top Right R-modules [J].J of Nanjing Univ Math Biquarterly,2000,17(1):26-33
[9] Demarco G,Orsatti A.Commutative Rings in which Every Prime Ideal is Contained in a Unique Maximal Ideal[J].Proc Amer Math Soc,1971,30(3):459-466
[10] 张国印.非交换环上的Zariski拓扑[J].金陵科技学院学报,2008,24(1):1-5
[11] 王景昕,张国印.环的幂等元与素谱的开闭集[J].金陵科技学院学报,2007,23(3):5-8
[12] 张国印.GELFAND商环和正规素谱[J].金陵科技学院学报,2007,23(2):1-4
[13] 张国印,王景昕.素子模及其伴随素理想[J].四川师范大学学报,2007,30(5):598-601
[14] Lu C P.Spectra of Modules[J].Comm Algebra,1995,23(10):3741-3752
[15] Kelly J P.General Topology [M].New York:Springer-Verlag,1950

