基于算子李代数的子代数结构研究

陆长安

陕西工商职业学院,陕西西安710119



基于算子李代数的子代数结构研究

陆长安

陕西工商职业学院,陕西西安710119

摘要:李代数是重要的非结合代数，对于代数结构的刻划，使用较多的是算子李代数结构，这也是李代数理论的重要组成部分。本文针对顶点算子代数的研究，提出一种基于算子李代数的子代数结构，由L1[σ]、L2[σ]两类子代数构造算子李代数g(G,M)[σ]，论述了向量空间的生成，并根据两类子代数的定理与结构证明，为顶点算子代数的研究工作提供理论基础。

关键词:李代数;代数结构;算子李代数;子代数

作为非结合代数的重要理论，李代数被广泛研究及应用，而算子构成的李代数，则是该领域使用较多的代数结构，因此对算子李代数的代数结构进行探讨研究，有着一定的实践意义.当前研究较多的算子李代数结构是g(G,M)与g(G,M)[σ]，例如Andrea、Ando等人使用算子李代数g(G,M)对无扭量子环面李代数进行刻划[1,2]，Gordina等人使用算子李代数g(G,M)刻划了部分无限维李代数的顶点算子[3]，也有学者对算子李代数g(G,M)[σ]进行构造[4,5].此次研究提出了基于算子李代数g(G,M)[σ]的子代数构造，分别为L1[σ]和L2[σ]两类子代数，并采用实例深入探讨了算子李代数g(G,M)[σ]的子代数结构，从而为顶点算子代数的研究工作提供理论基础.

1　顶点算子代数向量空间的生成

向量空间的计算是研究顶点算子代数的基本步骤，此处假设M为一个正整数集，C×的允许子群为G，顶点算子代数的向量空间为V，根据李代数理论，可得以下方程：

式（1）中，a,bϵG,i,jϵM，形式变量为z，xij(k,a,b)ϵEndV.

设顶点算子代数的向量空间为算子李代数g(G,M)[σ]，该向量空间由1和顶点算子的系数构成，其中顶点算子的系数表达式为(a,b, z)，1≤i,j≤M,a,bϵG，根据文献X可知，算子李代数结构之

一为g(G,M)[σ].

若a1a2≠b1b2，可以得出下式：

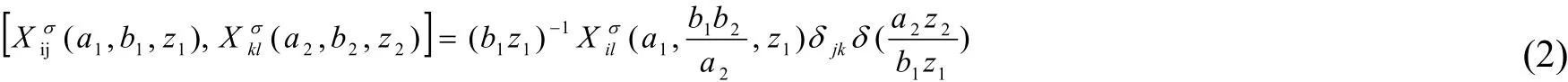
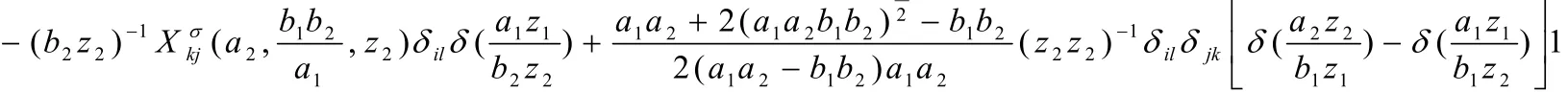
1

若a1a2=b1b2，可以得出下式：

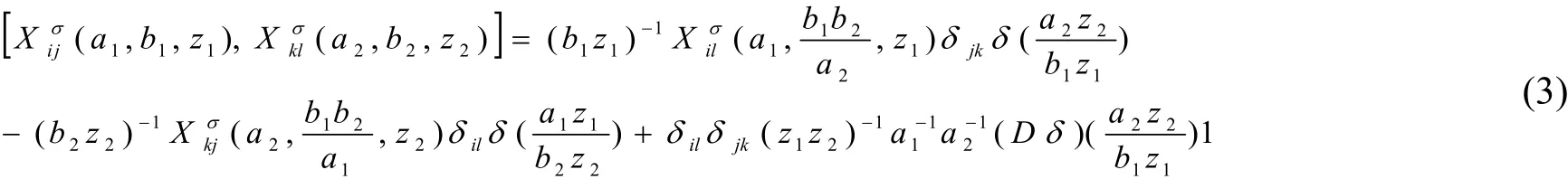
当M,N(≥2)为整数时，G=(ξ,q)为C×的允许子群，其生成条件有2个：（1）非单位根q(≠0)；（2）N次本原单位根ξ.文献X对算子李代数g(G,M)[σ]的代数结构进行了深入讨论，此次研究基于前人的理论，提出g(G,M)[σ]子代数的结构推断.

2　算子李代数的子代数结构推理结果

定义1：根据Yσ=(a,b,z),a,bϵG的系数生成的算子李代数g(G,M)[σ]的子代数称为L1[σ].

定理1：子代数L1[σ]的代数结构如下：

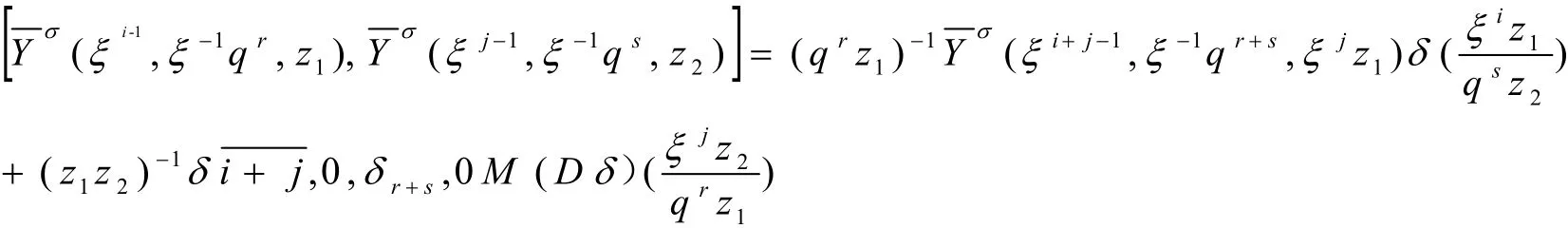
则算子李代数g(G,M)[σ]的子代数L1[σ]是由顶点算子代数的系数生成的，系数表达式为：

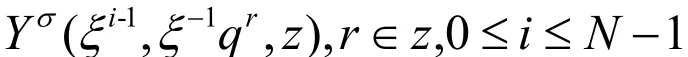
由式（1）和式（2）可知：

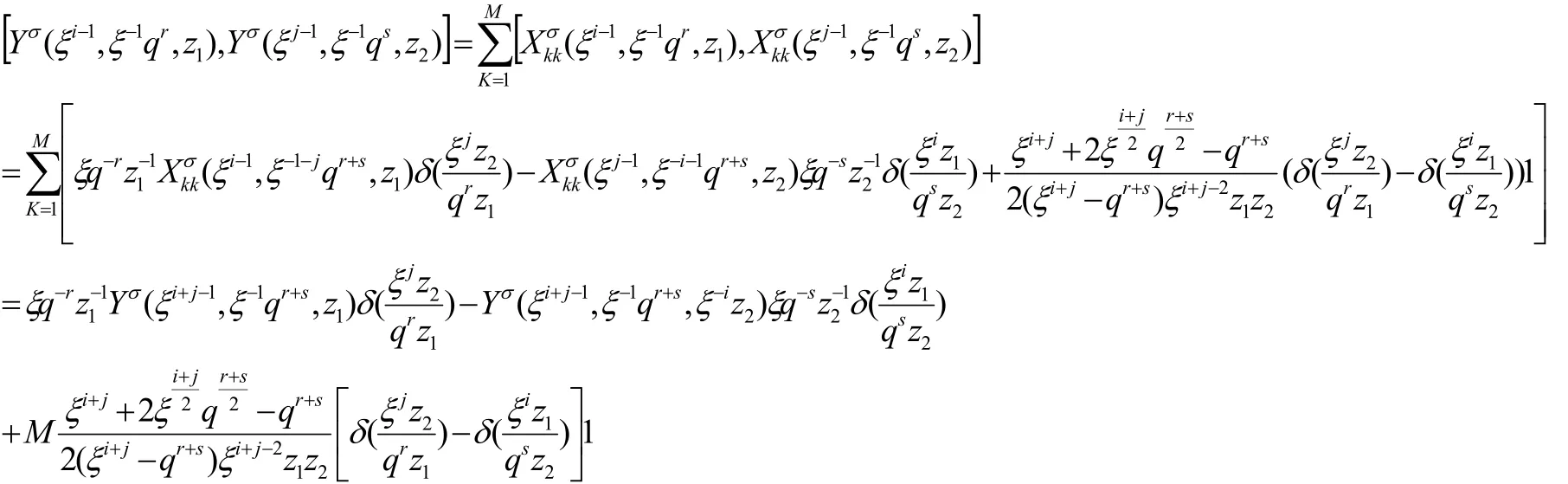
（2）若r+s=0，且i+j=0(mod N)，则：

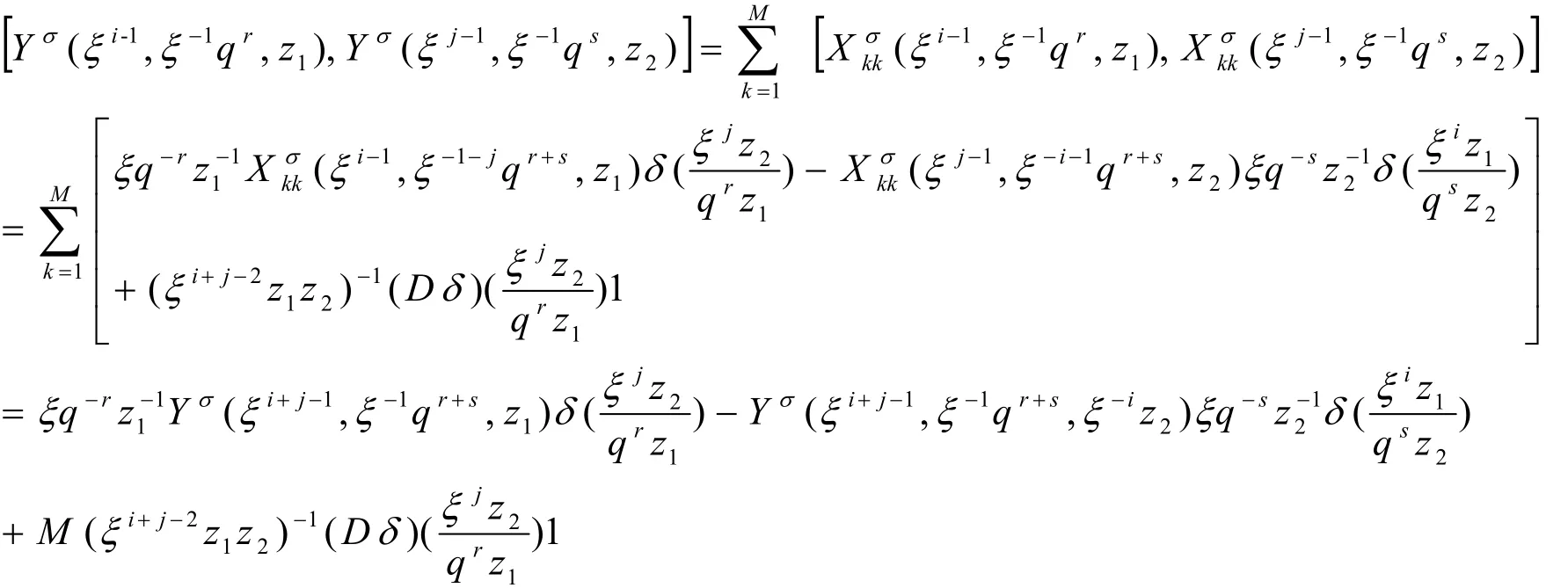
根据以上推算，设：

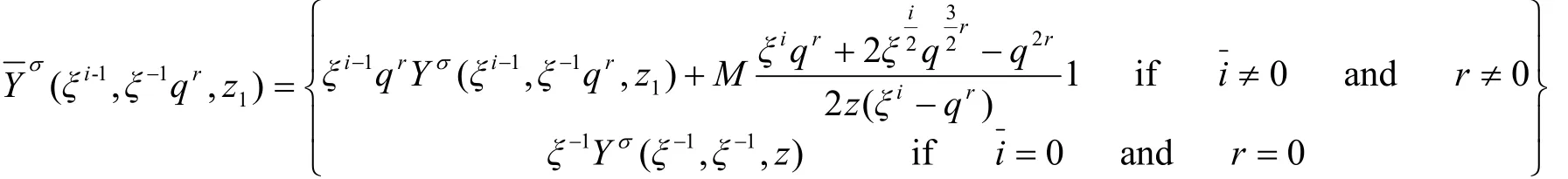
由此可知，定理1成立.

设g(‹q›,M)[σ]=span{1 and xij(m,1,qr)|m,rϵZ,1≤i,j≤M}

定义2：L2[σ]=span{1,xij(Nm,1,qr)|m,rϵz,1≤i,j≤M}

定理2：L2[σ]作为算子李代数g(‹q›,M)[σ]的子代数，并且与算子李代数g(‹q›,M)[σ]同构，根据相同结构的映射：

定理3：设m,n,r,sϵZ, i≠0(modN)，1≤k≠l≤M，可得出下式：

证明：由式（1）和式（2）可知：

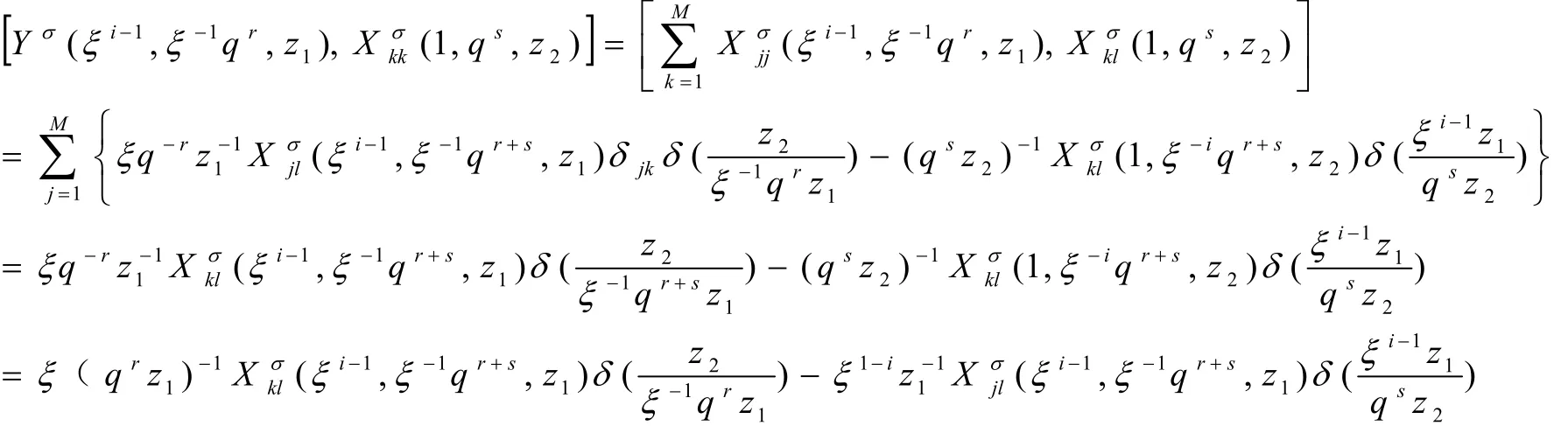
根据以上推断，定理3成立，令：

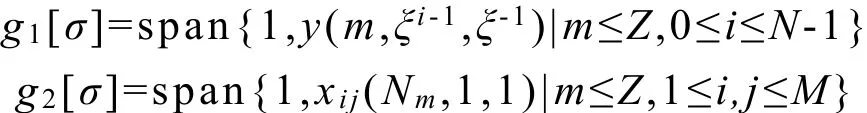
则：g1[σ]ϵLi[σ]ϵg(‹ξ,q›,M)[σ],i=1,2

定理4：算子李代数g(‹ξ,q›,M)[σ]的子代数g1[σ]和g2[σ]分别表示level M、level N的扭仿射李代数ĝlN(C)[σ]和ĝlM(C)[σ].

证明：令：

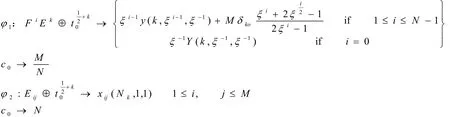
根据文献6的推论1,2[6]，可知定理4成立.

参考文献

[1] Andrea B. An ODE's Version of the Formula of Baker, Campbell, Dynkin and Hausdorff and the Construction of Lie Groups with Prescribed Lie Algebra[J]. Mediterranean journal of mathematics, 2010,7(3):105-108

[2] Ando H. Yasumichi M. Lie group-Lie algebra correspondences of unitary groups in finite von Neumann algebras[J]. Hokkaido Mathematical Journal, 2012,40(1):66-70

[3] Gordina M. Melcher T. A subelliptic Taylor isomorphism on infinite-dimensional Heisenberg groups[J]. Probability Theory and Related Fields, 2013,155(2):321-325

[4] Martini A.Analysis of joint spectral multipliers on Lie groups of polynomial growth[J]. Annales de l'Institut Fourier,2012,62(4):395-398

[5] Sun Siling, Ma Xiaofang. Lie Subalgebras in a Certain Operator Lie Algebra with Involution[J]. Acta Mathematica Sinica English Series, 2011,27(8):214-219

[6]李立,王辉.扭量子环面李代数LQ[σ]的代数结构[J].数学的实践与认识,2011,41(9):225-228

Study on the Sub-algebra Structure Based on Operator Lie Algebra

LU Chang-an

Shanxi Business College, Xi’an 710119, China

Abstract:The Lie algebra is important non-associative algebra, its algebraic structure to be used more is the operator Lie algebra, it is an important part of the theory of lie algebra. According to the research of vertex operator algebra, this paper put forward a kind of sub-algebra structure based on operator Lie algebra structure, L1[σ]、L2[σ] two kinds of sub-algebra structure made of operator Lie algebra g(G,M)[σ] to discuss the generation of vector space and take the theorem and structure of two classes of sub-algebra as the proof to provide the theoretical basis for the research work of vertex operator algebra.

Keywords:Lie algebra; algebraic structure; operator lie algebra; sub-algebra

作者简介:陆长安(1960-),男,河北省景县人,汉族,副教授,研究方向:高等数学、初等数学教学与研究.E-mail:lucaan@163.com

收稿日期:2014-06-20修回日期: 2014-07-02

中图法分类号:O171

文献标识码:A

文章编号:1000-2324(2015)04-0618-03