Parametric Instability Analysis of Deepwater Top-Tensioned Risers Considering Variable Tension Along the Length

ZHANG Jie, and TANG Yougang



Parametric Instability Analysis of Deepwater Top-Tensioned Risers Considering Variable Tension Along the Length

ZHANG Jie, and TANG Yougang*

,,,300072,

Parametric instability of a riser is caused by fluctuation of its tension in time due to the heave motion of floating platform. Many studies have tackled the problem of parametric instability of a riser with constant tension. However, tension in the riser actually varies linearly from the top to the bottom due to the effect of gravity. This paper presents the parametric instability analysis of deepwater top-tensioned risers (TTR) considering the linearly varying tension along the length. Firstly, the governing equation of transverse motion of TTR under parametric excitation isestablished. This equation is reduced to a system of ordinary differential equations by using the Galerkin method. Then the parametric instability of TTR for three calculation models are investigated by applying the Floquet theory. The results show that the natural frequencies of TTR with variable tension are evidently reduced, the parametric instability zones are significantly increased and the maximum allowable amplitude of platform heave is much smaller under the same damping; The nodes and antinodes of mode shape are no longer uniformly distributed along the axial direction and the amplitude also changes with depth, which leads to coupling between the modes. The combination resonance phenomenon occurs as a result of mode coupling, which causes more serious damage.

deepwater risers; parametric instability; variable tension; modecoupling

1 Introduction

It is known that a sinusoidally varying coefficient in the stiffness term of a mass-spring system can result in system instability. This phenomenon is called parametric instability. Parametric instability of slender marine structures (such as cables, risers and tethers) is caused by fluctuation of its tension in time (Brouwers, 2011; Zhang., 2010; Wang and Xie, 2012). In oil production riser is installed between wellhead at the sea bed and floating platform. The heave motion of floating platform induces a fluctuation in the axial tension of the riser. A possible and undesirable phenomenon is the excitation of a transverse vibration caused by this fluctuation. The fluctuating tension might destabilize the straight equilibrium of the riser and cause it to vibrate at a dangerously high level which creates serious damage to structure, and thus cause environment pollution and economical loss (Kuiper., 2008; Yang and Li, 2009).

Parametric instability of offshore cables, risers and tethers has received close attention of researchers in the past. Hsu (1975) was one of the first who analyzed parametric resonance for offshore cable applications, he studied the role played by the velocity square damping of the fluid in limiting the amplitude growth of such an unstable mode. Patel and Park (1995) studied dynamic behavior of buoyant platform tethers assuming a constant tension over the height and considering combined lateral and axial excitation at the top. The partial differential equation, governing the transverse motion of a tether, is reduced by them to a set of Mathieu equations with the help of the Galerkin method. Simos and Pesce (1997) studied dynamic behavior of TLP tethers considering the linearly varying tension along the tether length. The equation of motion is governed by a parametric Mathieu equation and the natural modes of lateral vibration are obtained in terms of Bessel functions. A comparison between the proposed dynamic model and the one presented by Patel shows that tension variation plays an important role in the stability analysis. However, they did not consider the coupling between the modes. Chandrasekaran. (2006) used the same method presented by Simos for investigating dynamic behavior of TLP tethers, and they concluded that TLP tethers with higher initial pretension are more stable in deep water. Xu(2011) used L-P (Lyapunov-Poincareper), modified L-P and harmonic balance methods to study parametric instability of long slender marine structures.Fujiwara(2011) performed a large-scale experiment in water with a Teflon tube of 28.5m long that was parametrically excited at the top.

Tension in the riser is typically assumed to be constant over the length. However, tension actually varies linearly from top to bottom due to the gravity. The aim of this study is to find the effects of variable tension on parametric instability of deepwater top-tensioned riser (TTR).

2 Assumptions and Equations

The heave compensator is modeled as a pre-tensioned vertical spring with a stiffness that is much lower than the axial stiffness of the riser. At the bottom, the connection between the riser and the wellhead is modeled by a hinge as shown in Fig.1.

Fig.1 Simply supported riser.

The equation of motion governing the transverse displacement(,) of the riser from its straight vertical equilibrium as a function of depthand timecan be written as:

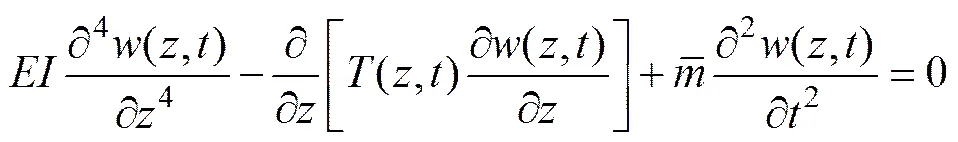
whereis the bending stiffness of the riser,is the mass per unit length of the system (riser with internal fluid and added mass), and(,) is the effective tension in the riser of the form:

, (2)

whereWis the submerged weight of the riser per unit length;Tis tension force at riser top with the formT=topWz(topbeing a dimensionless pretension factor which is generally varied between 1.1 and 1.6, and is taken to be 1.3 in this paper); In Eq.(2)is the stiffness of the heave compensator with the form=WL/10 (Kuiper., 2008);and Ω are the amplitude and frequency of platform heave respectively.

Assuming that the connection of the heave compensator to the riser can be modeled as a hinge, the boundary conditions at the ends of the riser are given as:

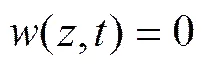
Theth natural frequency is given as (Zhang and Tang, 2014):

. (4)

Theth mode function for the low modes is given by (Senjanovic, 2006; Zhang and Tang, 2014):

whereTis tension force at riser bottom.

3 Parametric Instability of the Riser

Eq. (1) is reduced to a system of ordinary differential equations by using the Galerkin method. A solution to Eq. (1) is written in the form:

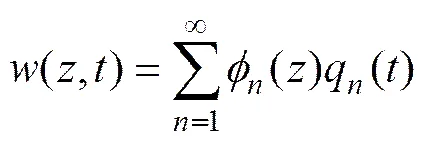
In a mathematically simplified form, Eq. (1) yields (Yang and Li, 2009):

wherefare coupling factors with the form:

, (). (8)

The damping caused by the surrounding water leads to an extra term in the set of differential equations (Brugmans, 2005):

whereis damping coefficient andis mode dependent coefficient:

, (10)

whereφmaxis the maximum value of displacement amplitude of the mode.

Eq. (9) can be approximated by a finite system of 2first-order coupled equations:

whereandstand for, respectively, the mode number and the total number of modes considered. For the present case:=8.

In matrix notation, Eq. (9) can be written as Eq. (12):

Stability of Eq. (12) can be studied by employing the Floquet theory (Tang and Shao, 2012).

4 Numerical Examples

4.1 System Parameters and Basic Calculations

The values of the system parameters are shown in Table 1. The natural frequencies and mode shapes of TTR are calculated by Eqs. (4) and (5) as shown in Table 2 and in Fig.2.

Table 1 Base set of system parameters

Table 2 Natural frequencies

Tension in the riser decreases linearly from top to bottom due to the effect of gravity, which is equivalent to reducing the stiffness of the riser. Comparing with the constant tension, the natural frequencies of riser with variable tension are evidently reduced. The single mode shape of the rise is no longer a standard sine function. The nodes and antinodes are no longer uniformly distributed along the axial direction, and the antinode amplitude increases as the depth increases. The mode shapes of riser with variable tension are not orthogonal; this leads to a coupling between the modes.

The frequency Ω varies between 0.2 and 2.2rads−1, since the period of wave generally varies between 3 and 20s. It shows that the excitation frequency range is concentrated in the low-order mode frequencies of TTR.

Fig.2 The fifth mode shape.

4.2 Parametric Instability Analysis of TTR

In order to study the effects of variable tension on parametric instability of risers, three calculation model are established:

(a) Constant tension uncoupling model:

(b) Variable tension uncoupling model:

. (14)

(c) Variable tension coupling model:

According to the Floquet theory, the numerical simulated results of stability charts are shown in Figs.3 and 4, where the shaded parts are instability zones.

Fig.3 Stability chart without damping.

Fig.4 Stability chart with damping (c=0.27).

4.2.1 Constant tension uncoupling model

The parametric resonance of the simply supported riser with constant tension occurs in the case of Ω=2ω/, whereis natural number which defines the order of the instability zones. For larger value of, the instability zones are smaller. The low-order instability zones are more important than high-order instability zones which are very narrow and become smaller rapidly if a linear damping term is introduced to these zones (Brugmans, 2005).

Fig.3(a) shows that the first order instability zones of the first six modes (Ω=2ω,=1, 2,…, 6) are excited in the frequency range (Ω=0.2–2.2rads−1). The spectrum of natural frequencies of TTR is very dense due to the high slenderness ratio, which leads to overlapping of different instability zones, and that is why the second order instability zones of the even number modes (Ω=ω,=2, 4, 6, 8) are not exhibited. In fact, the second and other higher order instability zones are difficult to be exhibited accurately due to the overlap of instability zones and the unsufficient accuracy of numerical algorithm.

Fig.4(a) shows that the linear damping can effectively reduce instability zones, especially the high-order instability zones rapidly decrease. Therefore, the effect of high-order instability zones can be negligible due to the existence of damping. The first order instability zones are the focus of research.

4.2.2 Variable tension uncoupling model

Comparing Fig.3(a) with Fig.3(b), the instability zones of variable tension uncoupling model are evidently increased. The natural frequencies of TTR are evidently reduced and more dense due to the variable tension (as shown in Table 2). Therefore, more modes are excited in the frequency range (the first order instability zones of the first eight modes are excited in Fig.3(b)), and there is more overlap of instability zones.

Comparing Fig.4(a) with Fig.4(b), the maximum allowable amplitude of platform heave for variable tension model is much smaller than for constant tension model under the same damping. This suggests that in the case of variable tension model, small platform heave may excite parametric resonance. Thus the stability cases for con- stant tension model might be unstable for variable tension model.

4.2.3 Variable tension coupling model

Fig.3(c) shows many instability zones, and this is the result of taking into account the coupling between the first eight modes. The combination resonance phenom- enon occurs as a result of mode coupling (Ω=2ω: the primary resonance; Ω=ω+ω: the combination resonance).

Fig.4(c) shows that linear damping can effectively reduce combination instability zones, and the maximum allowable amplitude of platform heave is a little smaller than the value as shown in Fig.4(b). However, the effects of mode coupling on parametric instability of risers can not be negligible.

According to Fig.4(c), assuming=1.90m, Ω=25(the parameters lie on the dividing line between stability zones and instability zones), initial values:,. The time functions of the vibration of riser are shown in Fig.5.

Fig.5 Time functions.

Fig.5 shows that the fifth-order mode is excited, and the other modes are characterized by a relatively large amplitude of the time function due to the mode coupling. This phenomenon is different from the results of constant tension model presented by Yang and Li (2009). They concluded that only one mode is excited, and the other modes are not excited in which the time functions go to zero.

The dynamic response is numerically simulated consi- dering combination of the first eight modes as shown in Fig.6. The maximum deflection of TTR is 0.23m(at 282s) and the corresponding maximum bending stress is 1.62MPa. The maximum deflection and bending stress are at the bottom of the riser. It can be seen that the vibration response of TTR at the bottom is greatly influenced by the axial tension which decreases as the depth increases.

Fig.6 Deflection of TTR.

Assuming=2.77m and Ω=4+5, initial values:q=1,. The Time functions under this parametric excitations are shown in Fig.7.

Fig.7 shows that the 4–6th modes are characterized by a relatively large amplitude of the time function when combination resonance occurs. The maximum deflection of TTR is 0.64m(at 260s) and the corresponding maximum bending stress is 4.69MPa, suggesting that the combination resonance is more dangerous.

5 Conclusions

Tension in the riser decreases linearly from top to bottom due to the effect of gravity, and this is equivalent to reducing the stiffness of the riser. Comparing with the case of constant tension, there are two differences:

1) The natural frequencies of riser with variable tension are evidently reduced, and more modes are excited in the frequency range. The parametric instability zones are significantly increased and the maximum allowable amplitude of platform heave is much smaller under the same damping.

2) The nodes and antinodes of mode shape are no longer uniformly distributed along the axial direction and the amplitude also changes with depth, which leads to coupling between the modes. The combination resonance phenomenon occurs as a result of mode coupling. The combination resonance causes more serious damage, which should be avoided.

Acknowledgements

The study is supported by the National Natural Science Foundation of China (51239008, 51279130, 51079097) and Science Fund for Creative Research Groups of the Na- tional Natural Science Foundation of China (51021004).

Brouwers, J. J. H., 2011. Asymptotic solutions for Mathieu instability under random parametric excitation and nonlinear damping., 240: 990-1000.

Brugmans, J., 2005.Parametric instability of deep-water risers. Master thesis. Delft University of Technology, Netherlands.

Chandrasekaran, S., Chandak, N. R., and Anupam, G., 2006. Stability analysis of TLP tethers., 33: 471-482.

Fujiwara, T., Uto, S., and Kanada, S., 2011. An experimental study of the effects that change the vibration mode of riser VIV. In:. OMAE2011-49677, Rotterdam, Netherlands, 487-492.

Hsu, C. S., 1975. The response of a parametrically excited hanging string in fluid., 39: 305-316.

Kuiper, G. L., Brugmans, J., and Metrikine, A. V., 2008. Destabilization of deep-water risers by a heaving platform., 310: 541-557.

Patel, M. H., and Park, H. I., 1995. Combined axial and lateral responses of tensioned buoyant platform tethers., 17 (10): 687-695.

Senjanovic, I., Ljustina, A. M., and Parunov, J., 2006. Natural vibration analysis of tensioned risers by segmentation method., 61 (5): 647-659.

Simos, A. N., and Pesce, C. P., 1997. Mathieu stability in the dynamics of TLP’s tethers considering variable tension along the length., 29: 175-186.

Tang, Y. G., and Shao, W. D., 2012. Study of vibration instability of TTR with varying axial force and tension ring. In:. OMAE2012-83072, Rio de Janeiro, Brazil, 57-63.

Wang, J. R., and Xie, B., 2012. Mathieu instablity study of a deepwater semi-submersible platform.,29 (10): 347-353 (in Chinese).

Xu, W. H., Wu, Y. X., Zhong, X. F., He, Y., Liu, P. L., and Feng, X. H., 2011. Methods for parametric excitation instability analysis of slender flexible cylindrical structures in offshore engineering., 30 (9): 79-83 (in Chinese).

Yang, H. Z., and Li, H. J., 2009. Vibration analysis of deep-sea risers under parametric excitations., 28 (9): 65-69 (in Chinese).

Zhang, J., and Tang, Y. G., 2014. Further analysis on natural vibration of deep-water risers., 18 (1-2): 165-171 (in Chinese).

Zhang, L. B., Eltaher, A., and Jukers, P., 2010. Mathieu instability of TTR tension fluctuation due to VIV. In:IOPF2010-2002, Houston, USA.

(Edited by Xie Jun)

DOI 10.1007/s11802-015-2374-x

ISSN 1672-5182, 2015 14 (1): 59-64

© Ocean University of China, Science Press and Springer-Verlag Berlin Heidelberg 2015

(April 24, 2013; revised June 8, 2013; accepted July 11, 2014)

* Corresponding author. E-mail: tangyougang_td@163.com