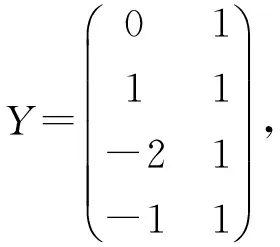求解广义模糊线性系统的一类迭代法
顾 颖, 陈 新
(1.宿迁学院 教师教育系, 江苏 宿迁 223800; 2.南京师范大学 数学科学学院, 江苏 南京 210046)
求解广义模糊线性系统的一类迭代法
顾 颖1, 陈 新2
(1.宿迁学院 教师教育系, 江苏 宿迁 223800; 2.南京师范大学 数学科学学院, 江苏 南京 210046)
研究给出了求解广义相容模糊线性系统和不相容系统的一类迭代法,给出两个数值例子.结果表明,无论系统相容与否,该迭代法都能快速求出它的极小解或极小最小二乘解.
广义模糊线性系统; 极小解; 极小最小二乘解; 迭代法
0 引言
考虑广义模糊线性系统
Ax=b
(1)
其中系数矩阵A为m×n实矩阵,未知项x和右端项y为模糊数.当(1)为相容系统时,求出它的解,否则考虑最小二乘解.在这所有的解或最小二乘解中,人们最为关注的又是具有极小范数的那一个.
B.Asady[1]通过嵌入式方法,将该问题转化为一个求解2m×2n线性方程组
(2)
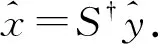
SX=Y
(3)
通过求解此矩阵方程得到当式(1)或式(2)为相容系统时的极小解,但该迭代法的一个主要的局限性是它对不相容的系统是无效的.
本文以矩阵方程(3)为模型,给出了求解广义模糊线性系统的一种算法.该算法的特点是无需事先判断系统是否相容,便可直接求出它的极小解或极小最小二乘解.
1 预备知识
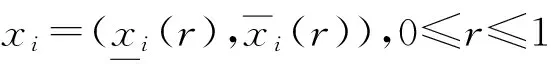
其中1≤i≤m则称模糊数向量x=(x1,x2,…,xn)T为广义模糊线性系统的一个解.
将广义模糊线性系统转化为矩阵方程(3),由广义模糊线性系统(1)中的第i个方程
可得如下方程组
其中1≤i≤m,0≤r≤1,于是,广义模糊线性系统(1)等价转化为一个未知量
右端向量
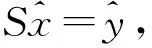
若aij≥0,则
Sij=Si+m,j+n=aij,Si+m,j=Si,j+n=0.
若aij<0,则
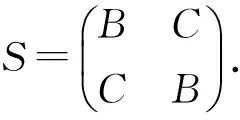
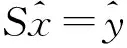
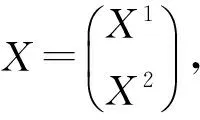

因此矩阵方程SX=Y又可写作
(4)
2 主要结果
对于形如AX=B的矩阵方程,王金林[5]等人给出了求解它的一种有效算法.本文中广义模糊线性系统转化所得的矩阵方程(3)或(4)是它的一种特殊情况.现将该算法应用于式(3)或(4),从而得到求解广义模糊线性系统(1)或(2)的一种算法.
对于式(3),构造迭代格式
Xk+1=Xk+βSTRk,Rk=Y-SXk,k=0,1,2,…,
初始值X0=STD(D为任一2m×2矩阵);β为一非零实数,当且仅当β满足

(5)
时,迭代法收敛,其中⊗表示克罗内克乘积.为了节约存储空间并减少计算量,现依据矩阵方程(3)的另一种形式(4)书写该算法.
算法: 1)选取满足式(5)的实数β和任意两个m×2阶矩阵D1,D2;
3)令k=1;
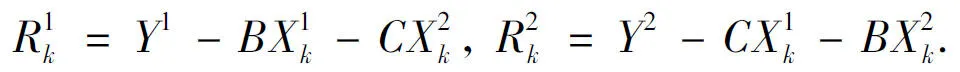
如果‖Xk+1-Xk‖ 根据文[5]的结论,若矩阵方程(3)或(4)相容,迭代法所得结果为它的极小解,否则为极小最小二乘解.据此可知,若广义模糊线性系统(1)或(2)相容,则本算法所得结果为其极小解;若不相容,则结果为其极小最小二乘解.相比 Feng[4]的算法,该算法无需事先判断系统相容与否便可直接进行求解. 例1[2]考虑2×3相容广义模糊线性系统 在Zheng[2]等人通过计算系数矩阵S的Moore-Penrose 逆求得该相容模糊系统的极小解.此处应用本算法,利用 Matlab 编程计算,只需迭代40次,耗时0.092016s便可得到如下近似解 其误差不超过1.0×10-7. 由此进一步得到原模糊线性系统的极小解为 若 Feng[4]的算法仅需3步便可得到如上精度的解,但是它仅对相容的广义模糊线性系统有效. 例2[3]考虑2×3不相容广义模糊线性系统 在 Wang[3]等人通过计算系数矩阵S的 Moore-Penrose 逆求得该不相容模糊系统的极小最小二乘解.此处应用本算法,利用 Matlab 编程计算,迭代40次,耗时0.118716s得到 其误差不超过1.0×10-7. 由此进一步得到原不相容模糊线性系统的极小最小二乘解为 因为这是不相容的系统,所以Feng[4]的算法对本例无效. [1]Asady B,Abbasbandy S,Alavi M. Fuzzy general linear systems[J]. Applied Mathematics and Computation,2005,169(1):34-40. [2]Zheng B,Wang K. General fuzzy linear system[J]. Applied Mathematics and Computation,2006,181(2):1276-1286. [3]Wang K, Zheng B. Inconsistent fuzzy linear system[J]. Applied Mathematics and Computation,2006,181(2):973-981. [4]Feng Y. An iterative method for fuzzy linear systems[J]. in: Fifth Interational conference on Fuzzy Systems and Knowledge Discovery (FSKD’08), IEEE, 2008,1(1):565-569. [5]王金林, 张帆.一类矩阵方程的迭代解法[J].南昌航空大学学报:自然科学版,2008, 22(1): 40-42. GU Ying1, CHEN Xin2 [责任编辑:李春红] AnIterativeMethodforSolvingGeneralFuzzyLinearSystems (1.Department of Teachers Education, Suqian College, Suqian Jiangsu 223800, China); (2.School of Mathematical Science, Nanjing Normal University, Nanjing Jiangsu 210046, China) It studies an iterative method for solving consistent and inconsistent general fuzzy linear systems. Two numerical examples are given to illustrate that the minimal solution or minimal least squares solution can be obtained quickly by this method no matter the system is consistent or not. general fuzzy linear systems; minimal solution; minimal least squares solution; iterative method 2015-03-29 国家自然科学基金资助项目(11271196); 江苏省教育厅自然科学研究基金资助项目(07KJD110094) 顾颖(1986-),女,江苏宿迁人,讲师,硕士,研究方向为数值代数. E-mail: guying-1986@126.com O241 : A : 1671-6876(2015)02-0100-04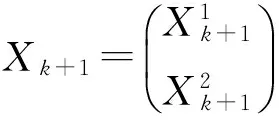
3 数值例子