一个数学结论的拓展及其应用

杨晓俊

（贵州省福泉市第一中学）

在中学数学教学中经常见到这样一个性质：等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高。关于此性质的证明有如下两种方法：

方法1：如（图1）利用面积，连结AP，两个三角形面积之和等于大三角形面积可得。

图1

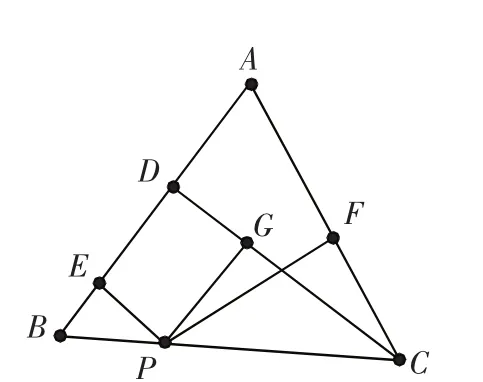
图2

方法 2：如（图 2）截长，作 PG垂直 CD于 G，易证 PE=DG，后证三角形CPG与三角形CPF全等，可得CG=PF，即得。

该性质是教学中经常遇见的命题，但是对该命题进行研究，发现该性质可以作如下拓展：等边三角形内（含边）任意一点到三边距离之和等于等边三角形的高。

对于这个拓展命题的证明，我们可以仿照原命题的证明方法进行，这里从略，下面主要列举原命题和拓展命题在数学竞赛题上的应用。

例1.如（图3），在矩形ABCD中，O是对角线AC，BD的交点，AB=3，AD=4，P是AD边上的一个动点，且PE⊥AC于E点，PF⊥BD 于 F点，则 PE＋PF=_________

解：作AG⊥BD于G点.在Rt△ABD中，BD=5.

∵△ABD是直角三角形，且AG是斜边BD上的高，

∴S△ABD=AB·AD=BD·AG，AG=2.4.

由四边形ABCD为矩形，可知OA=OD，即△OAD为等腰三角形.

∵P是底边AD上的任意一点，且PE⊥AC于E点，PF⊥BD于F 点，根据原命题有 PE＋PF=AG.即 PE＋PF=AG=2.4

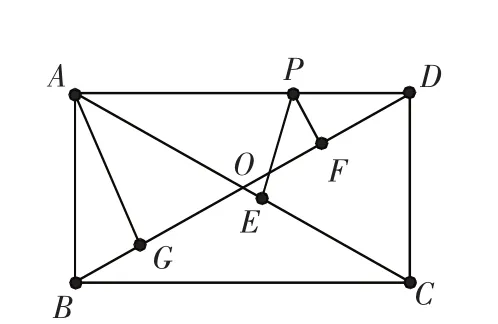
图3

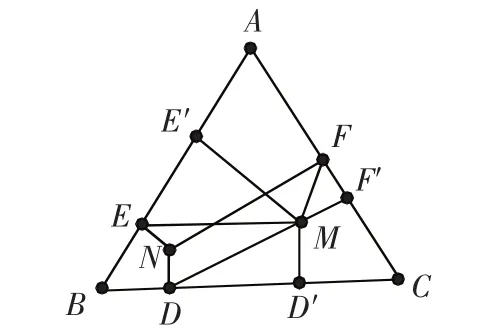
图4

例2.如（图4），已知等边三角形 ABC内有一点 N，ND⊥BC，NE⊥AB，NF⊥AC，D，E，F 都是垂足，M 是三角形 ABC 中异于 N的另一点，若 P1=ND+NE+NF，P2=MD+ME+MF，那么 P1与 P2的大小关系是

解：设△ABC高为h，过M点分别作BC、AB、AC的垂线，垂足分别是 D′、E′、F′

∵N 是等边三角形内一点，NE⊥AB，ND⊥BC，NF⊥AC，

根据拓展命题有 NE＋ND＋NF=h=P1，同理 MD′+ME′+MF′=h

又 ∵MD′≤MD，ME′≤ME，MF′≤MF（ 三个等号中最多有一个成立）

∴P1=NE+ND+NF=MD′+ME′+MF′＜MD+ME+MF=P2

∴P1＜P2

例3.如（图5），等边三角形ABC内有一点 P，过点P向三边作垂线，垂足分别是 S、Q、R，且 PQ=6，PR=8，PS=10，求△ABC 的面积。

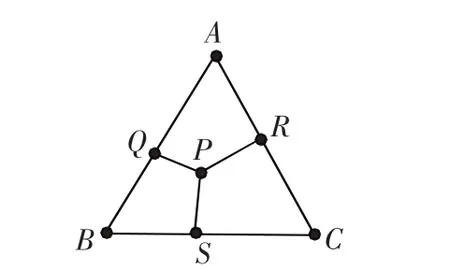
图5

解：设等边三角形边长为a，高为h，

则根据拓展命题有h=6+8+10=24

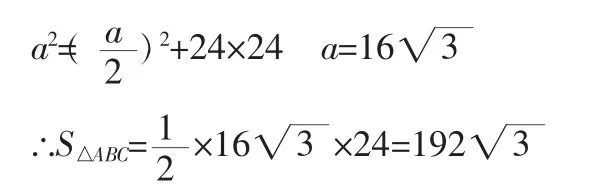
例4.如（图6），设P是等边三角形 ABC内任意一点，从点 P作三边的垂线 PD、PE、PF，点 D、E、F 是垂足，则

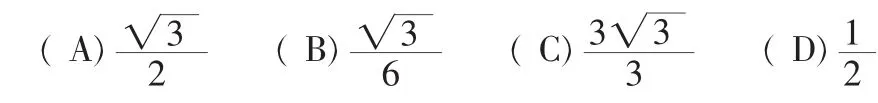
解：设等边三角形边长为a，高为h，

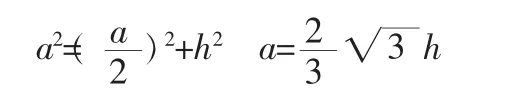
图6

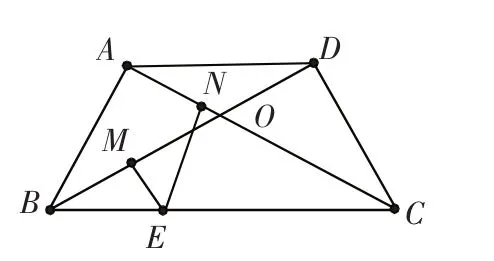
图7

例 5.如（ 图 7），在等腰梯形 ABCD 中，AD∥BC，∠ABC=60°，AB=AD=CD=2，E是 BC 上任意一点，EM⊥BD，EC⊥AC 于 N，求EM+EN的值

解：在等腰梯形 ABCD 中，AB=AD=CD=2，∠ABC=60°，

则容易得 BC=4，∠BDC=90°，

OB=OC，从而根据原命题有EM+EN=CD=2

学习数学，不能只记忆书本上的几条定理，应该将例题、习题中反映的性质做深入研究，争取做到融会贯通，举一反三，这种学习方法对于提高学生解题能力会有很大帮助。

朱克祥.初等几何研究［M］.高等教育出版社，2103-01-01.