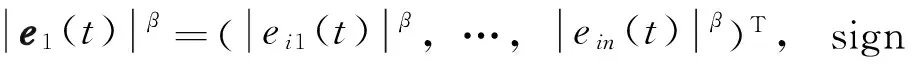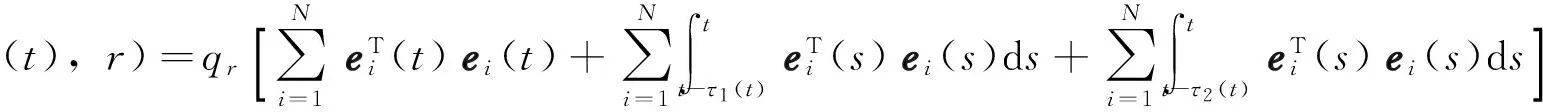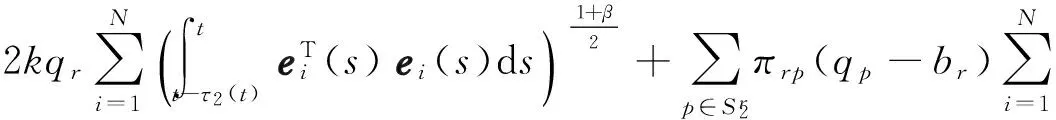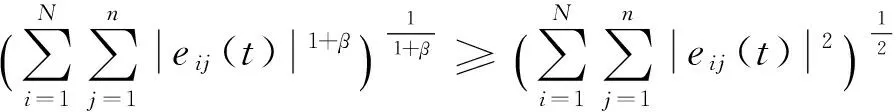具有马氏跳拓扑复杂网络的有限时间同步
李 娜,丰建文,赵 毅
深圳大学数学与统计学院,广东深圳 518060
具有马氏跳拓扑复杂网络的有限时间同步
李娜,丰建文,赵毅
深圳大学数学与统计学院,广东深圳 518060
摘要:考虑一类带有部分未知转移率,以及含有内部时滞和耦合时滞的马氏跳复杂网络的有限时间同步问题.通过构造适当的随机Lyapunov-Krasovskii函数,利用有限时间稳定定理以及矩阵不等式得到保证该网络在一个确定时间内达到同步的判据.有限时间同步意味着可获得最佳收敛时间及较好的鲁棒性和抗干扰性.数值模拟验证了所得理论结果的有效性.
关键词:复杂网络;马氏跳;时滞;转移率;有限时间同步;控制器
复杂网络是复杂系统的一种网络形式,是对复杂系统相互作用的一种本质抽象,普遍存在于现实世界中,如万维网、电力网、通讯网及生物网等[1-3].同步是指网络中耦合节点的动力学行为经过一段时间的演变最终达到相同的状态,是网络上典型的集体运动形式和网络结构导致的涌现现象,近年已成为网络科学的研究热点之一,受到不同学科研究者的广泛关注,并取得大量研究成果,这些研究大都涉及完全同步[4]、指数同步[5]、渐近同步[6]及广义同步[7]等的讨论.
上面所提及的网络同步指的都是当时间趋于无穷时达到的同步,然而,在工程领域却经常需要尽可能快地达到同步,即在一定的时间内达到同步,也就是有限时间同步[8-9].例如,在安全通信中通常需要在较短时间内恢复传递信号,以此来提高其有效性和保密性,所以有限时间同步不仅能在收敛时间内达到最佳性,而且对外部不确定因素具有更好的抗干扰能力,并能增强系统的鲁棒性[10-12].2010年,Yang等[13]首先讨论一类复杂网络的有限时间随机同步问题,2013年,他们又研究了非恒同不连续节点网络的有限时间同步[14].与此同时Mei等[15]研究了带有不确定参数驱动响应系统的有限时间结构识别和同步.但上述研究忽略了时滞,而时滞在现实世界中普遍存在[16],如电话通信,QQ联系时由于通信信道阻塞等多种原因是存在时间延迟的.近来的一些研究中也注意到时滞的影响,如Mei等[17]利用脉冲控制和间歇控制实现了带有耦合时滞的复杂动力网络的有限时间同步;Li等[8]对带有时变时滞的耦合网络有限时间同步问题进行讨论;Cui等[18]给出了带有部分未知转移率和内部时滞的马氏跳复杂网络的有限时间同步充分条件,但仅考虑了内部时滞或者耦合时滞.本研究考虑内部时滞和耦合时滞均存在且为时变的实际网络.另一方面,网络结构是随着时间演变在不断变化的,为使所研究的情形更加符合实际,现有研究引入马尔可夫链(简称为马氏跳)来描述网络的结构变化,即网络的结构只在有限个状态下发生变化,且由一种状态依一定概率变化到另一种状态,事实上,这种现象存在于现实网络中,如神经网络[19]、基因调控网络[20]及Hopfield网络[21]等.然而在大多数情况下,马氏跳网络的转移率是未知的,且对状态转移率的估计值可能引起网络的不稳定或降低系统的表现,最近得到一些有关不确定转移率的拓展结果[22-24],但上述这些工作中均要求不确定转移率是有界的.通过上述分析,对未知转移率无任何附加条件下考虑带有部分未知转移率的马氏跳复杂网络的有限时间同步是非常有意义的.
受相关研究启发,本研究考虑带有内部时滞(发生在节点内部的时滞)和耦合时滞(节点之间产生的时滞),且有部分未知转移率马氏跳复杂网络的有限时间同步问题,通过设计一系列控制器,根据有限时间稳定定理,经过严格的数学证明得到该类网络的有限时间同步判据.最后,通过数值模拟论证所得理论结果的有效性.
1模型描述与准备工作
考虑如下复杂网络模型:


τ2(t))),i=1,2,…,N
(1)



网络(1)的初始条件为
xi(z)=φi(z)∈C([-τ,0],Rn),
i=1,2,…,N
其中, τ=max{τ1,τ2}, C([-τ,0],Rn)表示从区间[-τ,0]映射到Rn的连续函数集.
网络(1)的孤立节点方程为

(2)
用s(t)表示式(2)满足初始条件s(t)=ψ(t),t∈[-τ,0]的解.其中, ψ(t)∈C([-τ,0],Rn).
本研究旨在通过设计适当的控制器使系统(1)在给定时间内同步到系统(2),为此首先给出文中所用到的定义、引理及假设.
定义1[18]马氏跳复杂网络(1)是有限时间同步的,若存在t*>0, 对任意的t≥t*,使
(3)
成立.
假设1[18]存在两个常数矩阵Θ=(θij)n×n和Φ=(φij)n×n, 其中, θij≥0, φij≥0, 使得系统(1)中的 f(t,xi(t),xi(t-τ1(t)))满足

∀x=(x1,x2,…,xn)T∈Rn,
y=(y1,y2,…,yn)T∈Rn, i=1,2,…,n.
(4)
注1若式(4)中τ1(t)=0, 则式(4)变为

引理2[17]对于∀x1, x2,…,xn∈Rn是任意向量, 0 2带有时滞的部分未知转移率马氏跳复杂网络的有限时间同步 为实现网络系统(1)在有限时间内同步,需要施加一些控制器ui(t), 这样被控制的网络系统为 (5) 记ei(t)=xi(t)-s(t), 根据式(2)和式(5),并注意到 A和 B的性质可得误差系统为 f(t,s(t),s(t-τ1(t)))+ τ2(t))+ui(t),i=1,2,…,N (6) 设计下述形式的控制器 (7) 在控制器(7)的作用下,我们讨论受控系统(6)在原点处的有限时间稳定.以下为本研究所取得的主要结果. 定理1若函数 f(t, xi(t), xi(t-τ1(t)))满足式(4),且以下不等式成立 (8) 【证】对任意的qr>1和r∈S, 选取如下随机Lyapunov-Krasovskii函数 (9) 根据伊藤公式,代入式(6)得 (10) (11) (12) E[LV(t, e(t),r)]≤ (13) 由引理2可得 则式(13)可改写为 由引理1知, E(V(t, e(t),r))在有限时间内趋于0,同时可估计同步时间的上界为 因此,误差向量 ei(t),i=1,2,…,N在时间t*内将会趋于0.此定理得证. 当内部时滞与耦合时滞都等于零时,相应的系统为 (14) 其孤立节点的方程为 (15) 设计控制器为 ui(t)=-ξi(r)ei(t)- (16) 由此可得如下推论. 推论1若假设1成立,且 (17) 注3定理1讨论了内部时滞与耦合时滞共存这类更符合实际的情形,如果令τ1(t)=0或者τ2(t)=0, 即仅考虑耦合时滞[15]或者内部时滞[18],那么对应改变设计的控制器即可,所以此处所得的结果推广了现有文献[15,18]的相关结果. 3数值模拟 考虑仅有两种模式的马氏跳系统(1),即r=2, 且系统有6个节点,每个节点的维数为二维.定理1中节点动力学f(·)定义如下[25] f(t, xi(t), xi(t-τ1(t)))= -Cxi(t)+Mg(xi(t))+Ng(xi(t-τ1(t))), 不失一般性,令外耦合矩阵定义如下: B(1)=A(1)= B(2)=A(2)= 图1 节点状态xij(t)随时间的演变Fig.1 (Color online) Variation of node state with time 图2 同步误差范数随时间的演变Fig.2 (Color online) Evolution of the norm of error variable over time 图3 同步误差范数随时间的演变Fig.3 Evolution of the norm of error variable over time 结语 本文研究了带有部分未知转移率的马氏跳复杂网络的有限时间同步问题,该系统具有可变的内部时滞和耦合时滞.通过设计一系列控制器及合适的Lyapunov-Krasovskii函数,利用线性矩阵不等式和有限时间稳定理论得到实现所研究系统在给定时间内达到同步的判据.通过数值模拟论证了所得结果的有效性. 引文:李娜,丰建文,赵毅.具有马氏跳拓扑复杂网络的有限时间同步[J]. 深圳大学学报理工版,2016,33(4):359-366. 参考文献/ References: [1] Boccaletti S,Latora V,Moreno Y,et al.Complex networks:structure and dynamics[J].Physics Reports,2006,424(4):175-308. [2] Pagani G A,Aiello M.The power grid as a complex network:a survey[J].Physica,2013,392(11):2688-2700. [3] Tang Jinjun,Wang Yinhai,Liu Fang.Characterizing traffic time series based on complex network theory[J].Physica,2013,392(18):4192-4201. [4] Wang Shuguo, Yao Hongxing, Bian Qiuxiang. Synchronization in complex networks with time-varying delays dynamical nodes via pinning control[J].Mathematical Problems in Engineering,2012,2012(1): 654742. [5] Sheng Li,Yang Huizhong.Exponential synchronization of a class of neural networks with mixed time-varying delays and impulsive effects[J].Neurocomputing,2008,71(16): 3666-3674. [6] Wang Zhanshan,Zhang Huaguang.Synchronization stability in complex interconnected neural networks with non-symmetric coupling[J].Neurocomputing,2013,108(5): 84-92. [7] Wu Xiaoqun,Zheng Weixing,Zhou Jin.Generalized outer synchronization between complex dynamical networks[J].Chaos,2009,19(1):193-204. [8] Li Dong,Cao Jinde.Finite-time synchronization of coupled networks with one single time-varying delay coupling[J].Neurocomputing,2015,166(31):265-270. [9] Huang Junjian,Li Chuandong,Huang Tingwen,et al.Finite-time lag synchronization of delayed neural networks[J].Neurocomputing,2014,139:145-149. [10] Bhat S P,Bernstein D S.Finite-time stability of continuous autonomous systems,SIAM[J].Control Optim,2000,38(3):751-766. [11] Li Shihua,Du Haibo,Lin Xiangze.Finite-time consensus algorithm for multi-agent systems with double-integrator dynamics[J].Automatica,2011,47(8):1706-1712. [12] Du Haibo,Li Shihua,Qian Chunjiang.Finite-time attitude tracking control of spacecraft with application to attitude synchronization[J].IEEE Transactions on Automatic Control,2011,56(11):2711-2717. [13] Yang Xinsong,Cao Jinde.Finite-time stochastic synchronization of complex networks[J].Applied Mathematical Modelling,2010,34(11):3631-3641. [14] Yang Xinsong,Wu Zhiyou,Cao Jinde.Finite-time synchronization of complex networks with nonidentical discontinuous nodes[J].Nonlinear Dynamics,2013,73(4):2313-2327. [15] Mei Jun,Jiang Minghui,Wang Jun.Finite-time structure identification and synchronization of drive-response systems with uncertain parameter[J].Communications in Nonlinear Science and Numerical Simulation,2013,18(4):999-1015. [16] Fei Zhongyang,Gao Huijun,Zheng Weixing.New synchronization stability of complex networks with an interval time-varying coupling delay[J].IEEE Transactions on Circuits and Systems II:Express Briefs,2009,56(6):499-503. [17] Mei Jun,Jiang Minghui,Xu Wangming,et al.Finite-time synchronization control of complex dynamical networks with time delay[J].Communications in Nonlinear Science and Numerical Simulation,2013,18(9):2462-2478. [18] Cui Wenxia,Sun Shaoyuan,Fang Jianan,et al.Finite-time synchronization of Markovian jump complex networks with partially unknown transition rates[J].Journal of the Franklin Institute,2014,351(5):2543-2561. [19] Yang Xinsong,Cao Jinde,Lu Jianquan.Synchronization of Markovian coupled neural networks with nonidentical node-delays and random coupling strengths[J].IEEE Transactions on Neural Networks and Learning Systerms,2012,23(1):60-71. [20] Zhang Wenbing,Fang Jianan,Tang Yang.Stochastic stability of Markovian jumping genetic regulatory networks with mixed time delays[J].Applied Mathematics Computation,2011,217(17):7210-7225. [21] Hopfield J J.Neurons with graded response have collective computational properties like those of two state neurons[J]. Proceedings of the National Academy of Sciences of the United States of America,1984,81(10):3088-3092. [22] Xiong Junlin,Lam J,Gao Huijun,et al.On robust stabilization of Markovian jump systems with uncertain switching probabilities[J].Automatica,2005,41(5):897-903. [23] Costa O L V,Val J B L,Geomel J C.Continuous time state feedback H2-control of Markovian jump linear system via convex analysis[J].Automatica,1999,35(2):259-268. [24] Kalyanasundaram S,Chong E K P,Shroff N B.Markov decision processes with uncertain transition rates: sensitivity and max hyphen min control[J].Asian Journal of Control,2004,6(2):253-269. [25] Gilli M.Strange attractors in delayed cellular neural networks[J].IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications,1993,40(11):849-853. 【中文责编:方圆;英文责编:木南】 中图分类号:O 193 文献标志码:A doi:10.3724/SP.J.1249.2016.04359 基金项目:国家自然科学基金资助项目(61273220,61373087) 作者简介:李娜(1990—),女,深圳大学硕士研究生.研究方向:微分动力学在复杂网络中的应用.E-mail:lina19900305@163.com Finite-time synchronization of Markovian jump complex networks Li Na, Feng Jianwen†, and Zhao Yi College of Mathematics and Statistics, Shenzhen University, Shenzhen 518060, Guangdong Province, P.R.China Abstract:A finite-time synchronization issue on a class of Markovian jump complex networks with partially unknown transition rates and time delays, including internal delay and coupling delay, is studied. With finite-time stability theorem and matrix inequality, some sufficient criteria have been proposed to guarantee the synchronization during a setting time by constructing the suitable stochastic Lyapunov-Krasovskii function. Since finite-time synchronization suggests optimality in convergence time, better robustness and better disturbance rejection properties, the results are important. The validity and effectiveness of the theoretical result are verified with several numerical simulations. Key words:complex networks; Markovian jump; time delay; transition rate; finite-time synchronization; controller Received:2016-03-10;Accepted:2016-05-25 Foundation:National Natural Science Foundation of China (61273220, 61373087) † Corresponding author:Professor Feng Jianwen.E-mail: fengjw@szu.edu.cn Citation:Li Na,Feng Jianwen,Zhao Yi.Finite-time synchronization of Markovian jump complex networks[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(4): 359-366.(in Chinese) 【电子与信息科学 / Electronics and Information Science】