发现几何本质，提高解题效率
——以立体几何动态问题中的隐性轨迹为例

沈新权 潘 虹

浙江省玉环县玉环中学 (317600) 浙江省嘉兴市第一中学 (314050)

发现几何本质，提高解题效率
——以立体几何动态问题中的隐性轨迹为例

沈新权 潘 虹

浙江省玉环县玉环中学 (317600) 浙江省嘉兴市第一中学 (314050)

立体几何是高中数学课程中的经典内容，它承载着培养学生逻辑推理和空间想象能力的不可或缺的任务，在高考中，立体几何也有着其极其重要的地位．空间向量的引入为求解立体几何问题提供了思维上的便利，正因为空间向量兼具几何和代数的双重身份，它成为了用代数方法解决立体几何问题的桥梁，因此从这个角度讲，空间向量无疑是处理立体几何问题的有力工具．在立体几何的教学中，我们感觉到用空间向量解决立体几何问题有时候也是一把双刃剑：对于有些立体几何问题，利用空间向量求解，虽然思路简单，但运算却比较繁杂，解题的效率不高；在实际教学中，有些老师为了在课堂上多讲解几个题目，在分析立体几何问题时，经常以空间向量处理立体几何问题的单一方法来引导学生，这种做法对传统立体几何的教学结构以及教学模式产生了很大的影响，长期下来，这样的教学方式势必与开设立体几何这一课程的目的背道而驰．因此，高中立体几何的教学中如何平衡好利用空间向量解决立体几何问题与充分借助图形的几何性质解决立体几何问题就显得尤为重要．

纵观历年各省市的高考数学试题，很多试题有一个显著的特点：想得多一点，就算得少一点；而想得少一点，就必须算得多一点．因此，解决同一个数学问题，有的解法需要10分钟时间，而有的解法可能只需要3-5分钟时间，这就是解题的效率问题，其中的差别就在于所使用的解题方法的不同．对于立体几何中的一些动态问题，这种差别尤为明显，如果我们在分析立体几何问题时能够发现问题中所蕴含的几何本质，这将会为问题的解决提供极大的便利．

一、发现动点圆的轨迹，利用投影计算线段长度比

立体几何中有一类问题，把一个平面图形按某种要求折起，转化为空间图形，进而研究图形在空间位置关系和数量关系上的变化，这类问题称为“平面图形的翻折问题”．处理这类题型的关键在于“以静制动，静观其变”，也就是画出折叠前后的平面图形与立体图形，抓住图形翻折前和翻折后的特征关系，并弄清折叠前后哪些发生了变化，依靠图形中的这些不变量和不变关系是解决折叠问题的关键．

在立体几何翻折问题中，动点的轨迹为圆，一般有两种情况，一种是互相垂直的线段的交点轨迹为圆；另一类是动点到两个定点的距离之比为常数(不等于1)的点的轨迹为圆(阿波尼斯圆)．

分析：本题是2016学年的台州期末考中的选择题第10题，这是一道立体几何中的最值问题，考试以后统计本题的正确率只有33.7%，大多数学生是想办法建立坐标系寻找函数关系式，从而求出其最大值，但因为运算比较复杂，有的学生虽然解出了答案，但为此浪费了不少宝贵的时间，也有不少学生因为不堪计算在考场上无功而返．

如果以角度为变量，我们还可以有如下的思路．

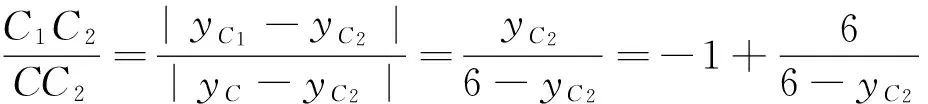
这里C2的轨迹为以CF为直径的圆，这是个隐性轨迹，同样是建立一个函数关系式，但代数与几何相结合，却比思路一简单得多．很多学生忽略了这个隐性轨迹，用思路一和思路二去解决固然可以，但计算量偏大．

二、探求动态图形中的不变元素，借助球的轨迹计算两点间距离的最值

与平面几何中定点到圆上的动点的距离的最值问题一样，立体几何中的两点间的距离的最值问题也可以借助空间中球的轨迹来解决，解决的关键在于能够发现问题中动点的轨迹为球．

例3 如图2，直线l⊥平面α，垂足为O，已知边长为2的等边三角形ABC在空间做符合以下条件的运动，A∈l,C∈α，则O，B两点间距离的最大值为___________．

利用几何法解决问题，关键要抓住几何要素，思路二与思路三中的隐形球可以简化代数法中的运算．

三、追踪动态图形中的圆锥轨迹，快速求解空间角的最值问题

对于一些平面图形的翻折问题，从动态的角度去看，就是平面图形绕着某一条直线旋转的过程中所形成的空间图形，因此平面图形的翻折问题在某种程度上看，其本质上是旋转问题，所以，求解时，如果我们恰如其分的利用隐藏在动态图形当中的圆锥的轨迹，这为问题的解决提供了技术的保障．

例4 如图3，在三棱锥P-ABC中，AB=AC=PB=PC=10,PA=8，BC=12，点M在平面PBC内，且AM=7，设异面直线AM与BC所成角为α，则cosα的最大值为( ).

无独有偶，2015年浙江省高中数学学业水平考试卷中一道选择题的压轴题也可以用这种方法得以轻松的解决．

例5 如图4，在菱形ABCD中，∠BAD=60°，线段AD,BD的中点分别为E,F，现将ΔABD沿对角线BD翻折，则异面直线BE与CF所成角的取值范围是( ).

利用动直线的圆锥轨迹不仅可以快速处理空间中角度的问题，还可以把问题从空间向平面转化，从而降低问题解决的难度．

例6 如图6，在ΔABC中，AB=BC=2,∠ABC=120°．若平面ABC外的点P和线段AC上的点D满足PD=DA,PB=BA，则四面体PBCD体积的最大值是 ．

分析与解：本题是2016年浙江省高考数学理科的第14题，求解四面体PBCD体积的最大值，可以考查学生的观察判断、空间想象、运算推理等能力，对学生有较高的能力要求．求解时，可以从建立坐标系利用代数法或是找到点线面的关系利用几何法去解决，这里不作详解．当没有理清立体几何错综复杂的点、线、面的位置关系时，我们会觉得立体几何很难下手，摸不到准确的方向．若当我们能看透本质，问题豁然开朗．

事实上，这里也藏着一个“隐性”轨迹．怎么发现？题干“PD=DA,PB=BA”可以把它看成一个翻折问题，又由“BP=BA=BC”联想到圆锥模型．取AC中点O，该圆锥以DO为轴，BA，BC为两条固定的母线，且∠ABC为圆锥母线所成最大角．在将面ADB翻折的过程中，可以把BP看成圆锥的一条

动母线，作出立体图形(如图7)，我们可以找到突破点：已知高BO为定值，要使VB-PCD达到最大，只须ΔPCD面积达到最大，从而空间问题转化成平面问题，难点迎刃而解．

以立体几何中的动态问题所隐藏的圆锥的轨迹为命题背景的高考试题比比皆是．如2016年浙江省高考数学文科第14题，2015年浙江省高考数学文科第7题，理科第8题等问题，虽然它们的表述方式表面上看起来都不太相同，但仔细分析，我们会发现这些问题所蕴含的几何本质是相同的，对这些几何本质的发现和挖掘，不仅可以提高学生的解题效率，更重要的是通过对立体几何问题的几何解决可以激发学生学习数学的兴趣，提高他们的逻辑推理能力和空间想象能力，从而可以达到学习立体几何的真正目的．

[1]周笔崇，施刚良.再谈浙江高考中的圆锥情结——以二道2016年浙江省数学高考文、理科卷填空题为例[J].中学教研(数学)，2016(8)：40-42.

[2]李建标.从考题中看动态立体几何中的圆锥情结[J].数学通报，2016(7)：40-42.