微积分的代数结构
郭 锂
(罗格斯大学纽瓦克分校 数学与计算机科学系, 新泽西 07102, 美国)
代数学,通常称抽象代数,是数学的一个分支.顾名思义,接触过抽象代数的大都认为代数学太抽象,不容易理解.事实上抽象是整个科学研究的基本特征,只不过代数学将其发挥到了极致.
自然科学的各个领域是对自然界的某个方面的集中研究,这就意味着只专注于自然界的某些特性而忽略它的其他性质,而这个过程恰恰是抽象过程.对随手捡起的一块石头,不同领域的科学家会得到不同的抽象,物理学家可能会注重石头的重量和动能,化学家可能会注重石头的分子结构,生物学家可能会注重石头里的微生物,地质学家可能会注重石头的生成结构.一旦有了被抽象出来的科学学科,就有了对科学学科本身的研究(即基础学科)和科学返回自然的应用(即应用学科和技术).我们应该强调的是科学的抽象化,不仅使得人类对自然的理解更深,而且更广.一个学科的成就可以应用于别的学科,这就像现在的云服务一样,你的文件一旦上传到云上,其服务对象就不仅限于你个人,而是网上的所有网友了.
如上所述,可以简单地说科学的各个学科是对自然界不同方面的抽象,进而各个科学学科都寻求规律性,而描述规律的基本方式是通过数学,包括逻辑、数字和方程.这样数学成为科学各个学科的抽象.从历史来看,古代的代数和数论抽象于计数,几何抽象于丈量;近代的微积分抽象于物理研究.一旦有了被抽象出来的数学,就有了对抽象数学的研究(即基础数学)和抽象数学返回科学学科的应用(即应用数学).数学抽象的威力是它的广泛应用,一个典型的例子是数论中的费马小定理.
定理1设p是一素数.对有限域Fp中任意元素x,有xp=x.
这是初等数论的一个基本结论,没有任何应用背景,在被发现的前300年中也没有得到任何应用,但是在20世纪70年代被应用于公开钥密码系统,现在已融入与人们日常生活密不可分的银行取款和网上金融等.
由此可以简单地说数学的各个分支是对科学各个领域的抽象.有了这些准备,代数的抽象就不奇怪了.它不仅是对科学学科的抽象,而且是对数学各个分支的抽象.代数的主要领域起源于数学分支的需求,除初等代数的古老起源外,结合代数起源于对不同数域的抽象,群论和域论的引进借助于研究方程用根式求解的伽罗华理论,李代数有明显的微分几何和微分方程背景,交换代数和模理论是作为数论和几何研究的需求建立起来的.同时数学的各个分支都以代数为载体结构、表述方式和研究方法.关于后者具体来说有代数数论、代数几何、代数拓扑和代数组合等.如同科学学科对自然界的抽象研究所起的作用一样,代数对其它数学分支的抽象研究也使得对其它数学分支的理解更深更广.
总体来说,有如下的抽象图
自然⟹科学⟹数学⟹代数.
本文介绍微积分的代数结构.如上所见,数学的大部分分支都有其代数研究.在文献中缺失的是代数分析,或代数微积分.从数学各分支的研究风格来看,这是可以理解的.如果把数学的各个分支排列在一条线上,代数和分析会排在2个极端,一个研究离散系统,一个研究连续系统.当然代数中有分析思维,如正向极限和逆向极限;分析中也有代数思维,如调和分析和同调群.但对微积分的系统代数研究,起源于本文要讨论的2个代数结构:作为微分分析代数化的微分代数和作为积分分析代数化的罗巴代数.
1 微分代数
1.1微分代数的概念如上所述,代数的特色是从其它领域中提取主要性质,抽象成各种各样的代数结构.代数结构通常由某些一元、二元和多元运算以及运算满足的关系决定.群论起源于求解多项式,结合代数起源于超复数和矩阵理论,其结合律是从各类数和函数的乘积关系提炼出来的,李代数是从切向量的括号积满足雅可比恒等式提炼出来的.
结合代数的一个基本例子是实值函数构成的代数.在此基础上,微分代数的模型是由可微函数构成的结合代数A上再附加上导子d,即微分算子.只考虑单变元的函数和导子.抽象的关键是对导子的抽象.首先,导子是线性的,即对任意的实数a、b和A中函数f、g有
d(af+bg)=ad(f)+bd(g).
其次,应该有刻画导子d在A上作用的特殊性质.容易想到熟知的莱布尼兹公式:对任意A中函数f和g有
d(fg)=d(f)g+fd(g).
注意到以上两式是可微函数的必要条件,但等式本身有意义并不要求a、b是实数或f、g是可微函数.可以把导子的这2个关键必要条件提炼出来作为抽象导子的定义.
定义1.1设R是交换环K上的结合代数.R上的微分算子定义为R上的线性算子d,且满足抽象的莱布尼兹公式.准确地说,对任意K中a、b和R中u、v有:
d(au+bv)=ad(u)+bd(v),
d(uv)=d(u)v+ud(v).
一结合代数R和其上一微分算子d构成一微分代数,记为(R,d),简记为R.
1.2微分代数的历史和意义微分代数起源于20世纪初Ritt[1]对微分方程的代数研究.经过Kolchin 和他们的学派[2-3]的研究,微分代数已经发展为包括微分伽罗华理论、微分代数几何、计算微分代数等分支的丰富领域,且有着广泛应用.吴文俊的数学定理机械化证明的著名工作[4-5]就是基于Ritt的微分代数工作.
作为一个练习,试考虑差分算子的代数化.更一般地,考虑算子的代数化.确定这些算子应该满足的代数方程,从而定义差分代数[6].
D:C(x)→C(x),
D(f)(x)∶ =f(x+1)-f(x)
Dh:C(x)→C(x),
Dh(f)(x)∶ =(f(x+h)-f(x))/h
2 罗巴代数的概念和例子
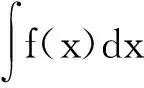
I:C(R)→C(R),
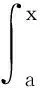
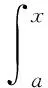
事实上,分部积分公式的证明恰是对上式求导并应用乘法公式得到的.上式微分算子和积分算子同时出现.为了专注对积分算子的研究,取

从而
F′(x)=f(x),G′(x)=g(x).
上式成为只涉及积分算子的等式


用算子形式改写并换项,得到
I(f)I(g)=I(fI(g))+I(I(f)g).
(1)
为了给后面的例子提供参考,用多元微积分的方法给出另一证明:上式左边的积分乘积

是在以s为横轴、t为竖轴的平面坐标系中正方形区域a≤s,t≤x上的积分.而第一象限由对角线s=t分为两部分,即上三角区域s≤t和下三角区域s≥t.容易验证f(s)g(t)在上三角区域的积分是

在下三角区域的积分是

因此根据积分区域的可加性即得到(1)式.
注意在(1)式中f和g可以取为任意代数中的元素,而I可以取为此代数上的任意线性算子.所以此式可以作为微积分中积分算子的代数化.由此给出如下定义:
定义2.1设R是交换环K上的结合代数.R上的积分算子定义为R上的线性算子I,且满足抽象的分部积分公式.准确地说,对任意K中a、b和R中u、v有:
I(au+bv)=aI(u)+bI(v),
I(u)I(v)=I(uI(v))+I(I(u)v).
一结合代数R和其上一积分算子I构成一积分代数,记为(R,I),简记为R.
或许是因为代数学家对分析的关注程度不够,历史上抽象的积分算子和积分代数的概念一直到上世纪末才由代数学家正式提出,而在此之前40年,比积分代数更广的罗巴(Rota-Baxter)代数概念已经由美国概率论学家Baxter[7]首先提出,并在美国著名分析学家Atkinson[8]和组合学家Rota等[9-11]的推动下得到发展,使得Rota-Baxter代数成为少见的由非代数学家多年主导研究的代数结构,这种状况一直到本世纪才得到转变,故在Rota-Baxter代数的概念被引进近60年后的今天,这个领域仍然是个新兴领域,更多的研究细节参见文献[12-13].
定义2.2设R为K上的结合代数,λ为K中固定元素.R上的权为λ的Rota-Baxter算子,或罗巴算子,定义为R上的线性算子P,且满足权为λ的Rota-Baxter等式.准确地说,对任意K中a、b和R中u、v有:
P(au+bv)=aP(u)+bP(v),
P(u)P(v)=P(uP(v))+P(P(u)v)+λP(uv).
一结合代数R和其上一Rota-Baxter算子构成一罗巴(Rota-Baxter)代数,记为(R,P),简记为R.
2.2罗巴代数的例子以下通过一些罗巴代数的例子来展示罗巴代数的广泛联系.
积分算子:如前所述,上限为变元的积分算子

是自然的权为零的罗巴算子.
求和算子:对正实轴上满足充分收敛条件的函数f(x)定义
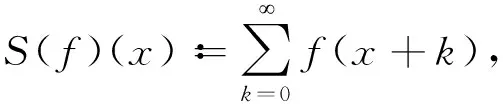
则算子S满足
S(f)S(g)=S(fS(g))+S(S(f)g)-S(fg),
故S是权为-1的罗巴算子,其证明如下:级数乘积S(f)S(g)可以表达为二重和
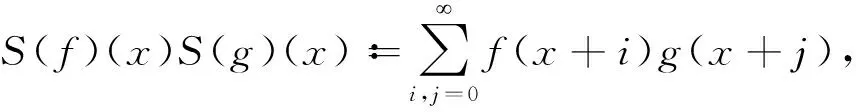
和式是在第一象限的具整数坐标的格点求和.而如同对(1)式的证明一样,对角线将第一象限划分为上三角i≤j区域和下三角i≥j区域两部分.对上三角区域i≤j中格点求和,并取k=j-i,得到
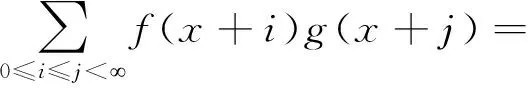
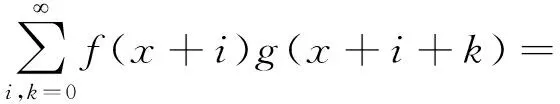

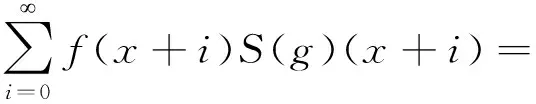
S(fS(g))(x).
同理对下三角区域j≤i中格点求和得
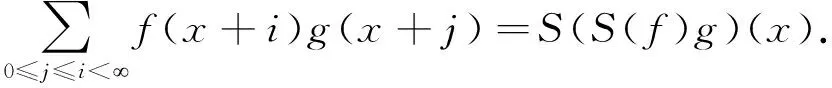
与对(1)式的证明不同,虽然在对角线上的二重积分为零,对其中格点的求和不为零,而上面对上三角和下三角区域的求和都包括对角线.因此对角线上的格点被算了2次,必须减去.而f(x)g(x)在对角线上整点的求和为
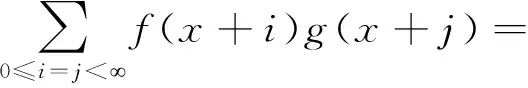
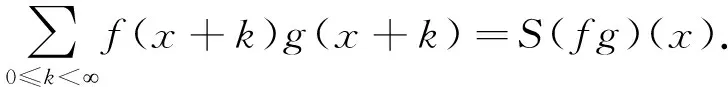
因此得到
S(f)(x)S(g)(x)=S(fS(g))(x)+
S(S(f)g)(x)-S(fg)(x).
这正是我们需要的.
部分和算子:如果想避免上一例子的收敛问题,可以考虑部分和序列.设A是一结合代数,设R=AN为在A中取值的无穷序列的集合,则R在分量加法、乘法和数乘下构成一个代数.对R中序列
r∶ =(r1,r2,r3,…,rn,…),ri∈A,
定义部分和序列
P(r)∶ =(r1,r1+r2,r1+r2+r3,…,
r1+…+rn,…),
则用以上例子同样的证明可得
P(r)P(s)=P(rP(s))+P(P(r)s)-P(rs).
因此P是权为-1的罗巴算子.如果调整部分和序列的定义为
P(r)∶ =(0,r1,r1+r2,…,r1+…+rn-1,…),
则P是权为1的罗巴算子.
上三角矩阵:在n×n矩阵代数中取R为上三角矩阵组成的子代数.对一上三角矩阵M,定义矩阵P(M)如下:其对角线元为矩阵M的所在行的元素之和;其非对角元为零,则P是权为-1的罗巴算子.
数乘算子:任取代数R和常数λ∈K.定义数乘算子
Pλ:R→R,r-λr,r∈R,
则易证Pλ是权为λ的罗巴算子.这个例子说明任意代数都有自然的罗巴代数结构.

即取其幂级数部分,则P是一权为-1的罗巴算子.
还有罗巴代数的很多其它例子,贯穿于概率论、组合数学、数论、泛代数和Operad等领域,这些例子说明罗巴代数和数学及物理有广泛的联系,这些联系既为罗巴代数的研究提供源泉和问题,也为罗巴代数的结果提供应用.
3 罗巴代数的结构
下面从2个方面介绍罗巴代数的结构.
3.1幂等罗巴算子和分解通过线性代数知道,如果向量空间V上线性算子P是幂等的,即P2=P,则V是P的核Ker(P)与像Im(P)的直和Ker(P)⊕Im(P).一个自然的问题是,如果代数R上线性算子P是幂等的,什么时候其子空间Ker(P)和Im(P)也是子代数呢?这个问题有个很完美的解答:
定理3.1设P是代数R上幂等线性算子.P是权为-1的罗巴算子当且仅当Ker(P)和Im(P)是R的子代数.
以上面提到的洛朗级数代数上的算子P为例.Ker(P)=t-1K[t-1]和Im(P)=K[[t]]都是R的子代数,故P是一罗巴算子.
证明设P是R上幂等算子.若P是权为-1的罗巴算子,则对Im(P)中元素P(r)和P(s)有
P(r)P(s)=P(rP(s))+P(P(r)s)-P(rs),
故P(r)P(s)在Im(P)中,由此得子空间Im(P)是R的子代数.同时易证算子Id-P也是权为-1的罗巴算子.因此Im(Id-P)也是R的子代数,但
Im(Id-P)=Ker(P),
所以Ker(P)是R的子代数.
反之,若Ker(P)和Im(P)是R的子代数,则由
R=Ker(P)+Im(P)
得R中r可表为r=r1+r2,其中r1在Ker(P)中,r2=P(r′)在Im(P)中.故
P(r)=P(r2)=P(P(r′))=P(r′)=r2.
同理R中s可表为s=s1+s2,其中s1在Ker(P)中,s2在Im(P)中.由此得到:
P(r)P(s)=r2s2,
P(rP(s))=P(r1s2+r2s2)=P(r1s2)+r2s2,
P(P(r)s)=P(r2s1+r2s2)=P(r2s1)+r2s2,
P(rs)=P(r1s1)+P(r1s2)+P(r2s1)+
P(r2s2)=P(r1s2)+P(r2s1)+r2s2.
因此
P(r)P(s)=P(rP(s))+P(P(r)s)-P(rs).
证毕.
3.2自由交换罗巴代数和洗牌乘法给定一代数结构,不管是半群还是代数,对其自由对象的研究是一个基本问题.由于罗巴代数是在代数上附加罗巴算子,自由罗巴代数的构造较为复杂.为简化起见,仅考虑权为零的情况.通过观察罗巴等式
P(r)P(s)=P(rP(s))+P(P(r)s),
注意到如同等式左边的2个像集中元素的乘积可以简化为右边的形式.这样罗巴代数中元素的一般形式中P的出现只有“串联”,如r0P(r1P(r2P(r3))),没有“并联”,如P(r1)P(r2)或P(r1)r2P(r3).再将P符号化,给出如下的自由交换罗巴代数的构造[14].
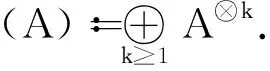
对Ш(A)中纯张量:
a=a0⊗a1⊗…⊗am,
b=b0⊗b1⊗…⊗bn.
通过对m+n归纳,递归地定义a◇b如下:
如m+n=0,即m=n=0,则a=a0,b=b0为A中元素.此时定义
a◇b∶ =a0◇b0=a0b0
为A中乘积.对任意给定k≥1,假定对满足m+n≤k的a和b,a◇b已定义,则对满足m+n=k+1的a和b,如m=0,则定义
a◇b∶ =(a0b0)⊗b1⊗…⊗bn.
如n=0,则定义
a◇b∶ =(a0b0)⊗a1⊗…⊗am.
如m>0且n>0,则简记
a=a0⊗a′,b=b0⊗b′.
定义
a◇b∶ =(a0b0)⊗(a′◇(1⊗b′)+
(1⊗a′)◇b′).
注意到在等式右边,由于a′的张量长度短于a,而1⊗b′的张量长度等于b,因此根据归纳假定a′◇(1⊗b′)是定义好的.同理,(1⊗a′)◇b′是定义好的.因此以上等式右边是定义好的.再通过双线性性质把a◇b扩展成任意2个张量的乘积.这一乘积满足结合律,使得Ш(A)成为一结合代数.再定义Ш(A)上一线性算子PA为
PA(a0⊗…⊗am)=1⊗a0⊗…⊗am.
从◇的定义得到PA是权为零的罗巴算子.在文献[15]中证明(Ш(A),PA)是A上的自由交换罗巴代数.通过洗牌乘法,◇有如下的显式构造:
给定2个张量:
a=a1⊗…⊗am,
b=b1⊗…⊗bm,
a和b的一个洗牌是张量
a1⊗…⊗am⊗b1⊗…⊗bn
的一个置换,即重新排序,使得a1到am的原有顺序和b1到bn的原有顺序保持不变.
例1a1⊗a2和b1⊗b2的洗牌为:
a1⊗a2⊗b1⊗b2,a1⊗b1⊗a2⊗b2,
a1⊗b1⊗b2⊗a2,
b1⊗b2⊗a1⊗a2,b1⊗a1⊗b2⊗a2,
b1⊗a1⊗a2⊗b2,
2个张量a和b的洗牌积aШb是它们的所有洗牌的和.
自由交换罗巴代数中的乘积◇和洗牌积的关系如下:对
a=a0⊗a′,b=b0⊗b′
有
a◇b∶ =(a0b0)⊗(a′Шb′).
知道了自由交换罗巴代数中的乘积就知道了任意罗巴代数中的乘积的共性.比如积分算子是罗巴算子的特例.通过洗牌积,很容易给出2个二重积分的乘积,而直接用积分是个相当复杂的计算:





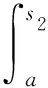

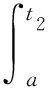



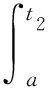

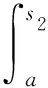
在没有交换性的限制下,自由罗巴代数的构造更为复杂,可以通过括号字、根树和Motzkin路径等组合方式得到,参见文献[13,16-17].
对具有多个罗巴算子的代数结构的研究还不多,见文献[18-19].另外,罗巴代数的变形,如Hom-罗巴代数的研究也刚开始,见文献[20-21].罗巴型代数的概念在文献[22]中引进,并与重写系统和Groebner-Shirshov基联系起来.
公开问题1构造多个罗巴算子的代数和Hom-罗巴代数的自由对象.
公开问题2完成对微分型代数和罗巴型代数的分类.
4 罗巴代数的应用
4.1量子场论重整化罗巴代数的一个重要应用是量子场论的重整化.量子场论通过费曼积分计算各类粒子相互作用的物理量,如动量和能量,但费曼积分的直接计算通常是发散的.经过多年的努力,物理学家得到一个相当复杂的过程,从发散的费曼积分中提取有限值,这个过程被称为重整化过程[23].量子电动力学(QED)的重整化使其成为描述电磁相互作用的“迄今为止最为精确的”物理理论.另一方面,由于重整化缺乏数学的严格基础,被比喻为人为地将垃圾扫到地毯下藏起来.还有一个恶搞物理学家的“名言”:我不怕无穷大,我把它切掉就行了.
通过Connes(1982年菲尔兹奖得主)和Kreimer的工作[24],重整化过程的组合结构在他们的代数Birkhoff分解的框架中得到准确的描述.同时,他们的代数理论也使得重整化这一物理理论得以应用于数学中其它的发散问题中.我们只介绍代数Birkhoff分解的基本形式.
设H为一联通分次Hopf代数.这意味着H既是代数又是余代数,且二者相容;同时H有一分次
也与H的代数和余代数结构相容;最后H0是一维的:H0≅K.较简单的例子是通常的一元多项式代数K[x],以次数分次
余乘为
⊗xk-i.
在量子场论中,H是由费曼图张成的向量空间,以费曼图的拼接为乘法,带有Connes-Kreimer定义的余乘.
再设(A,P)为权为-1的罗巴代数,其中P为幂等罗巴算子.这时也称A为幂等罗巴代数.由此有分解
A=A+⊕A-,
其中
A-∶ =P(A),A+∶ =(Id-P)(A).
在量子场论中,(A,P)为例中的洛朗级数代数,
A-=t-kK[t-k],A+=K[[t]].
代数Birkhoff分解定理设H是联通分次Hopf代数,(A,P)是权为-1的幂等罗巴代数.设φ:H→A为一代数同态,则φ有唯一的卷积分解
★φ+,
使得
φ-:H→K+A-,
φ+:H→K+A+
也是代数同态.这样有
φ+=φ-★φ.
φ+称为重整化,φ-称为抵消项.这个方程表述的意思是:φ中的发散通过φ-的发散消除了,得到收敛的φ+.
Connes和Kreimer的代数Birkhoff分解首先应用于量子场论的重整化.在文献[25-27]中,代数Birkhoff分解表述为罗巴代数中Atkinson分解的一个特例.通过代数Birkhoff分解,重整化方法被应用于多元Zeta值的重整化[28-30]、锥Zeta值的重整化和黎曼积分的重整化[31-32].最近,代数Birkhoff分解被用于阐述量子场论中的局部化概念[33].
公开问题3给出各种局部代数的结构.
4.2经典杨-巴克斯特方程和O-算子经典杨-巴克斯特方程是量子杨-巴克斯特方程的经典极限,是要求李代数的二阶张量满足的一个三阶张量方程,它在可积系统中起着重要作用.对自对偶李代数和反对称张量,经典杨-巴克斯特方程的(张量)解等同于李代数上的权零罗巴算子,叫做经典杨-巴克斯特方程的算子解.非常有趣的是引进罗巴算子的巴克斯特是美国数学家G. Baxter,而引进杨-巴克斯特的巴克斯特是澳大利亚物理学家R. Baxter.这看似巧合的更深层含义自20世纪80年代后一直被探讨着.由此得出修改杨-巴克斯特方程和O-算子等概念,更被移植到结合代数的范畴[34-38].近年来的研究[39-41]将权零罗巴算子推广的O-算子进一步延拓到权非零罗巴算子推广的权非零O-算子,得到O-算子和罗巴算子的共同推广.由此得到经典杨-巴克斯特方程和类似方程的更大一类解,并应用于可积系统.
一个基本问题是如何实现罗巴算子的量子化.它和量子杨-巴克斯特方程应该有何关系?
4.3对称函数和拟对称函数作为Rota构造的自由交换罗巴代数的应用,他用抽象的Spitzer恒等式给出了组合中有名的、联系基本对称函数和幂对称函数的Waring等式[9-10].他在多年前猜测[11],罗巴代数应该是对称函数的最一般和最自然的推广.之后,拟对称函数和罗巴代数的联系也建立起来[42].在文献[43-44]中,罗巴代数等同于左弱和弱拟对称函数,这给出对Rota问题的一个解答.
公开问题4Rota猜测的一般情形仍然没有解决.特别地对非交换罗巴代数和非交换对称函数及其推广的关系还有待进一步研究.
4.4Operad(代算) 罗巴代数与Operad的联系最初由Aguiar[45]发现.在随后的一系列工作中,这一联系得到各种扩展和推广[37,46-47].在文献[48-49]中建立了一般的Operad.这方面有一系列有关罗巴包络代数的庞加莱-伯克霍夫-维特(PBW)定理的问题有待解决,相关研究进展见文献[50-52].
在经典文献[11,53]中,Rota提出其它有关Rota-Baxter代数的问题和猜想.微积分的2种代数化在文献[54-56]中给出,分别称为微分Rota-Baxter代数和微积分代数.如何将微分代数和Rota-Baxter代数的广泛研究扩展到对这些代数结构是一个有待展开的研究方向.

