类比的魅力：从椭圆到双曲线

安徽省太湖中学(246400) 李昭平

从椭圆向双曲线类比,往往融直观想象、逻辑推理、数学运算等数学核心素养于一体,能有效培养学生的直觉思维能力、合情推理能力和探究证明能力.下面分享几个类比结论：从椭圆中的斜率乘积定值类比出双曲线中的斜率乘积定值;从椭圆的离心率公式类比出双曲线的离心率公式;从椭圆焦点三角形面积公式类比出双曲线焦点三角形面积公式.让我们从中体会类比的魅力.

1.斜率乘积定值的类比

例1 不经过原点O,且不平行于坐标轴的直线l与椭圆=1(a＞b＞0)有两个交点A(x1,y1),B(x2,y2),线段AB的中点为M,则相减得所以即

由此得到结论1：对椭圆,直线l的斜率与直线OM的斜率乘积为定值类比上述过程,推导双曲线的类似性质.

思路类比上述点差法,对双曲线实施同样的运算变形.

解析设双曲线是=1(a＞0,b＞0),A(x1,y1),B(x2,y2),线段AB的中点为M.由相减得所以即

由此得到结论2：对双曲线,直线l的斜率与直线OM的斜率乘积为定值

例2 经过原点O的椭圆b＞0)的弦是AB,P是椭圆上异于A,B的一点,且PA,PB的斜率都存在,设P(x0,y0),A(x,y),B(-x,-y),所以相减得于是

由此得到结论3：经过原点O的椭圆1(a＞b＞0)的弦是AB,P是椭圆上异于A,B的一点,则类比上述过程,推导双曲线的类似性质.

思路类比上述点差法,对双曲线实施同样的运算变形.

解 析设P(x0,y0),A(x,y),B(-x,-y),相减得于是kP A·kP B=

由此得到结论4：经过原点O的双曲线1(a＞0,b＞0)的弦是AB,P是双曲线上异于A,B的一点,则kP A·kP B=

2.离心率公式的类比

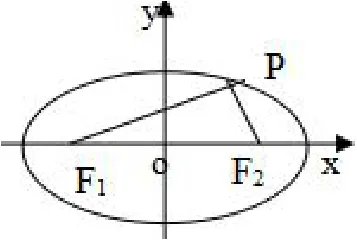
图1

例3 如图1,设椭圆的方程为=1(a＞b＞0),F1.F2是左右焦点.点P是椭圆上除长轴上两个顶点外的任意一点,且∠PF1F2=α,∠PF2F1=β,则所以所以所以

由此得到结论5：e=(椭圆离心率公式).将其推广到双曲线,写出推导的过程和结论.

思路从椭圆问题的证法出发,结合双曲线的定义,类比前行.

解析如图2,设双曲线的方程为0,b＞0),F1.F2是左右焦点.点P是双曲线左支上除顶点外的任一点,且∠PF1F2=α,∠PF2F1=β,则

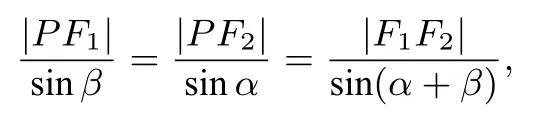
所以

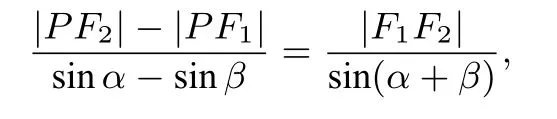
所以

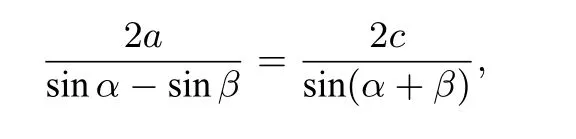
所以

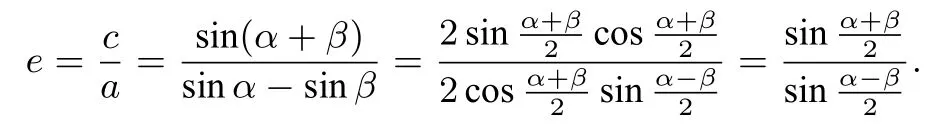
当点P是双曲线右支上除顶点外的任一点时,同理可以得到

由此得到结论6：e=(双曲线离心率公式).

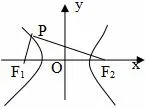
图2

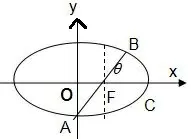
图3

例4 设点F是椭圆C的一个焦点,AB是过点F且不平行于对称轴的焦点弦,AB的倾斜角是θ,-→AF=m--→FB.

那么有结论7：(1)当焦点F在x轴上时,离心率(2)当焦点F在y轴上时,离心率

证明设椭圆方程为=1(a＞b＞0),如图3所示.不妨设F是右焦点,F(c,0),A(x1,y1),B(x2,y2),则由得y1=-my2,因为AB的斜率存在且不为零,设其为联立方程组消去x得到(a2+k2b2)y2+2kb2cy-b4=0.于是

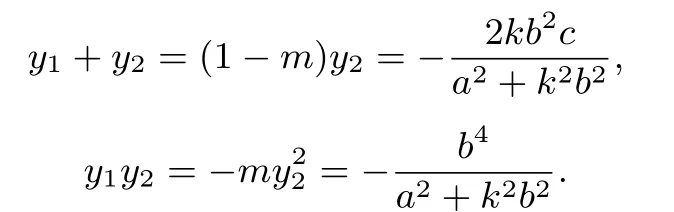
再消去y2得,-m·注意到则化简整理得到

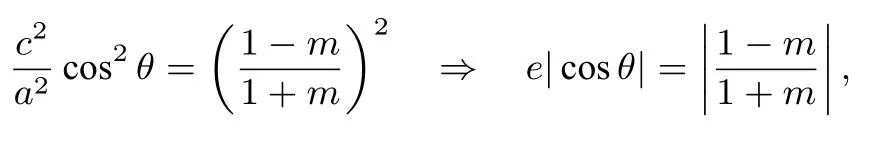
这是椭圆又一个离心率公式.可以将其推广到双曲线,得到同样的结论7：

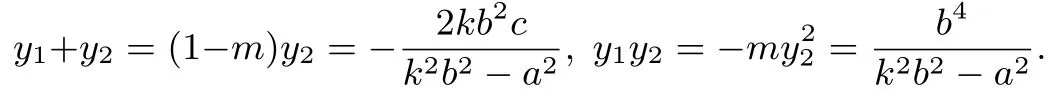
再消去y2,并注意到得 到,所以离心率若双曲线焦点F在y轴上,则以θ±代替中的θ,得e=

3.焦点三角形面积公式的类比

例5 如图1,设点P是椭圆=1(a＞b＞0)上除长轴端点外的任意一点,∠F1PF2=θ,|PF1|=m,|PF2|=n,则解得mn=于是

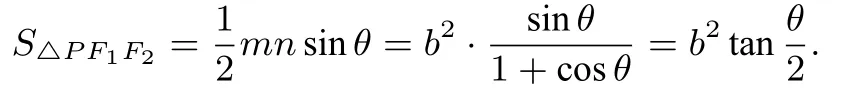
由此得到结论8：(椭圆焦点三角形面积公式).类比上述过程,推导双曲线焦点三角形的类似面积公式.

思路类比解椭圆中的焦点三角形,结合双曲线的定义运算变形.

解析结论：设|PF1|=m,|PF2|=n,则解得mn=于是

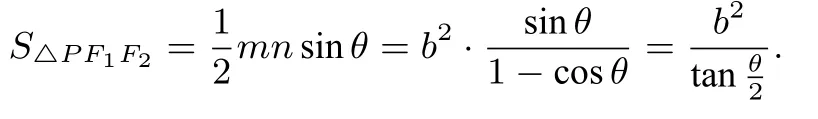
由此得到结论9：(双曲线焦点三角形面积公式).