基于椭圆光学性质的两个类包络现象的发现之旅
邵俊杰 李金兴
(1.北京邮电大学计算机学院 102206;2.浙江省萧山中学 311201)
圆锥曲线作为中学解析几何学习的重点,拥有悠久的历史和众多性质;其中圆锥曲线的光学性质极为特殊.人教A版教材介绍了光线经过圆锥曲线焦点时的光学性质;那么,那些不经过圆锥曲线焦点的光线又有何特性呢?
1 椭圆中的两个类包络现象
考虑到圆锥曲线中只有椭圆是封闭曲线,光会一直在内部反射,我们先对椭圆中的一般弦做出研究.根据初始光线与两焦点连线段的三种关系:初始光线经过某焦点、初始光线与焦点连线段不相交、初始光线与焦点连线段相交但交点非焦点,分别讨论光线的反射性质.
1.1 过椭圆焦点的光线性质
引理1设F1,F2分别是椭圆的两个焦点,P是椭圆上任意一点,则从F1发出的光线经过P点处椭圆反射后的反射光线经过点F2.
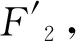
由此可见,如果初始光线沿过焦点的弦(非长轴),则经过椭圆反射后会通过另一个焦点,不断反射后交替地通过两个焦点.
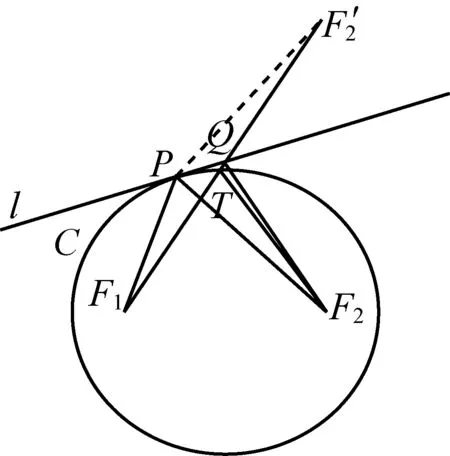
图1
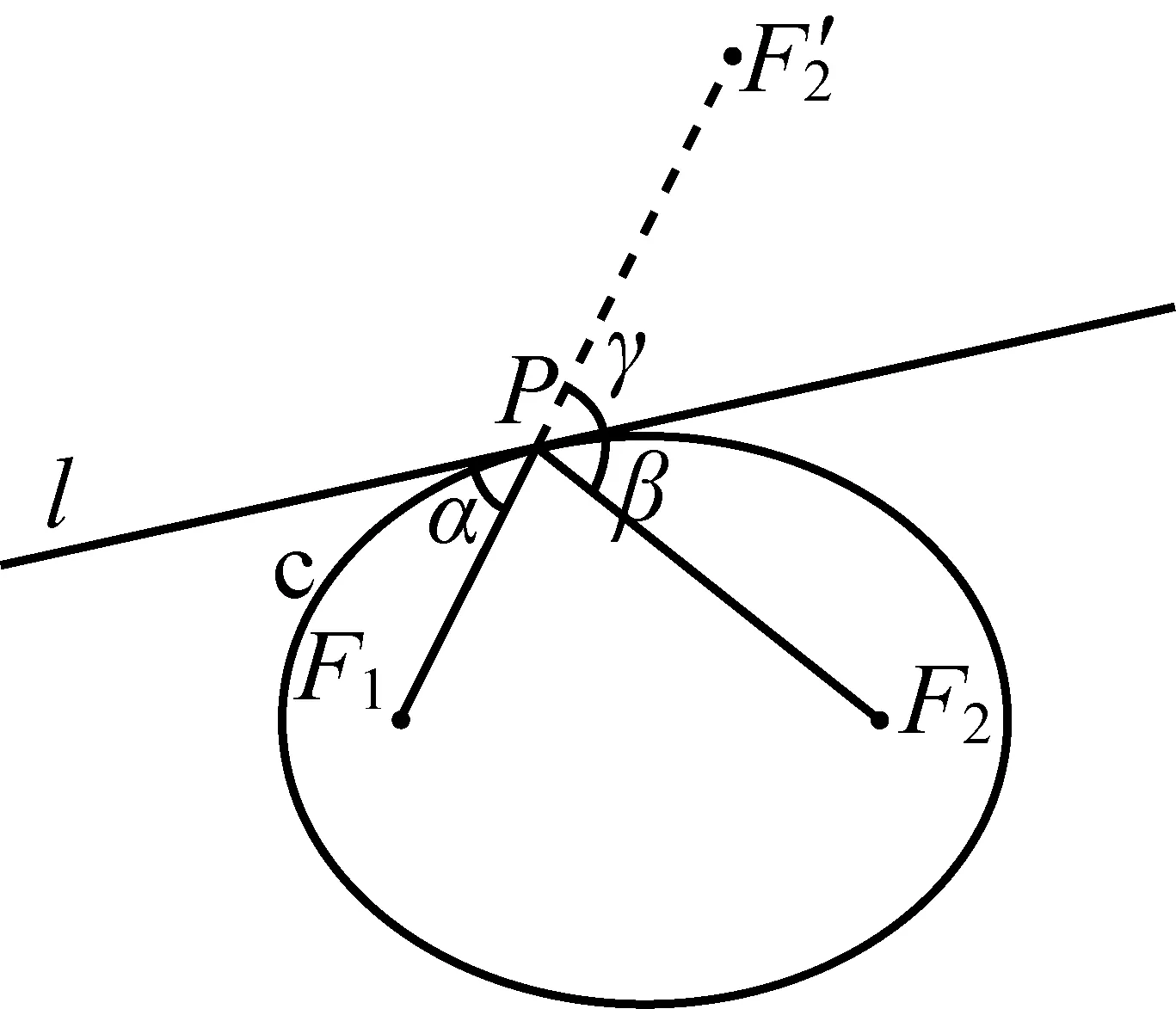
图2
1.2 初始光线与椭圆两焦点连线段不相交时的光学性质
为使证明过程简洁,我们先来证明几个引理.
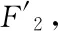
引理3椭圆C以F1、F2为焦点,A、B为C上两点,l1、l2分别为椭圆C在A、B点处的切线,F为l1与l2的交点,则∠AFF1=∠BFF2(如图3).
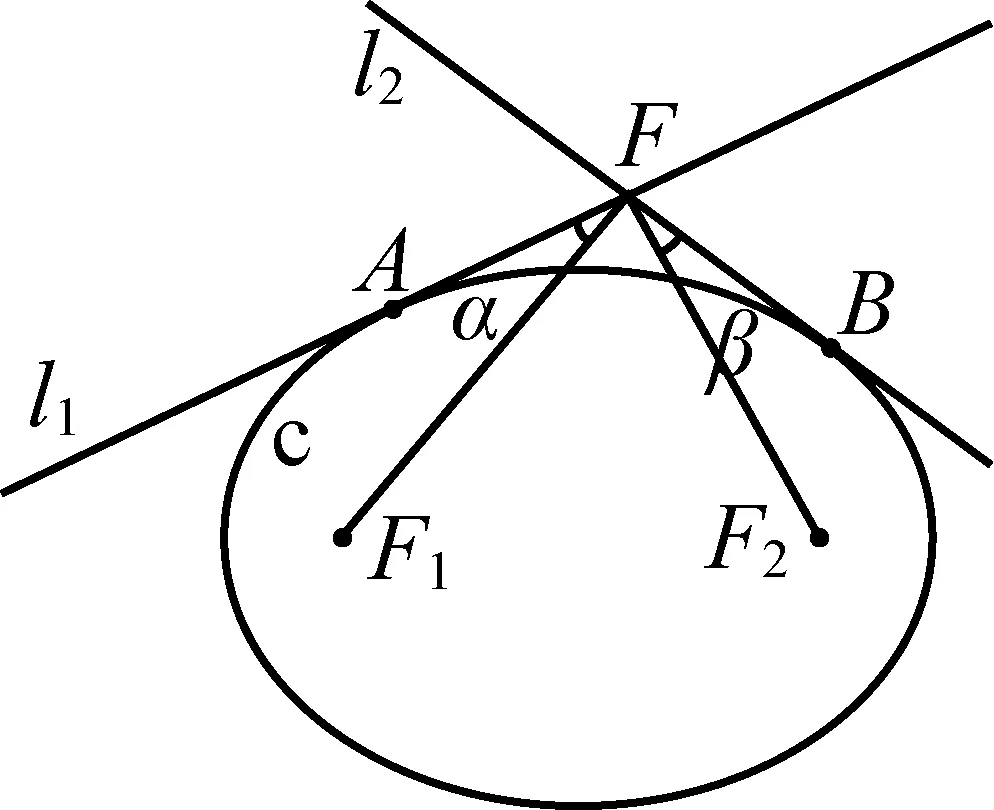
图3

图4
由上述引理可得,当初始光线与椭圆焦点连线段不相交时有如下结论:
定理1如图5,椭圆C1以F1、F2为两焦点,椭圆C1的弦S1S2与线段F1F2不相交,从S1发出的光线S1S2经椭圆C1反射后反射光线为S2S3,则S1S2和S2S3均与另一个以F1、F2为焦点的椭圆C2相切.
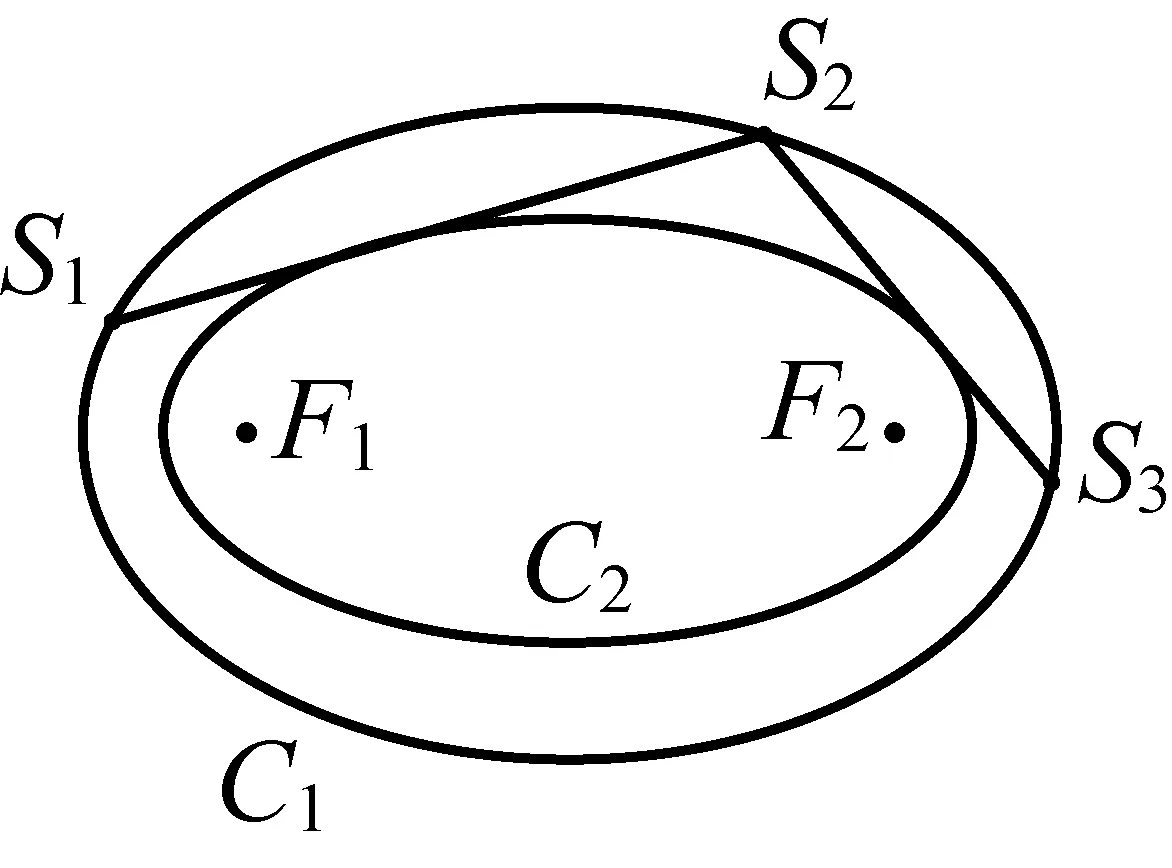
图5
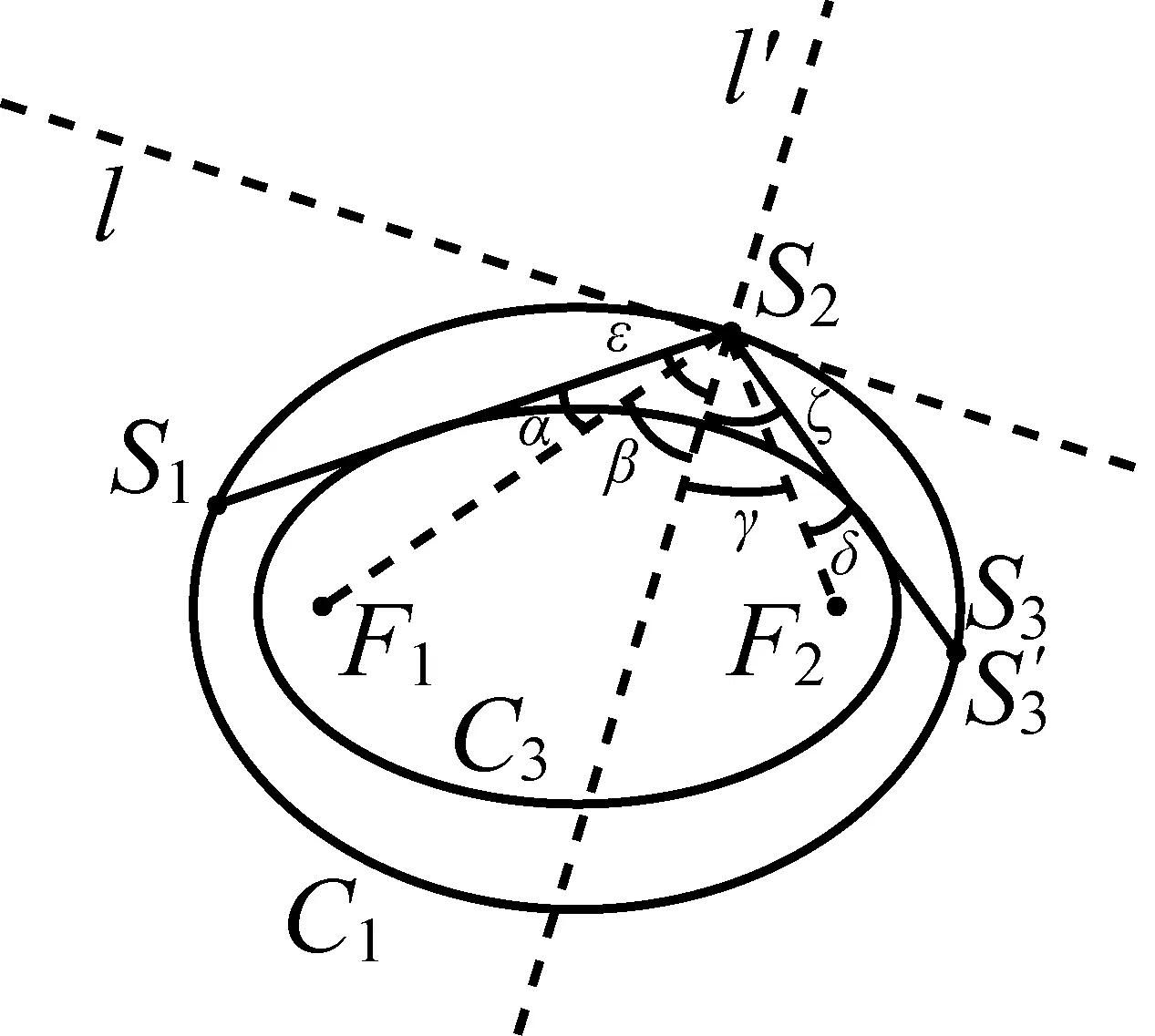
图6
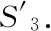

于是可知,设椭圆C0内部初始光线所在直线为l0,经椭圆C0反射n次后的反射光线所在直线为ln.当l0与椭圆C0焦点连线段不相交时,由定理1得,可设l0与l1同与椭圆C1相切,l1与l2同与椭圆C2相切,……,ln与ln+1同与椭圆Cn+1相切…;其中C1,C2,…,Cn+1,…均与C0同焦点.因此C1,C2共焦点且与同一条直线l1相切,故C1,C2为同一个椭圆,记作椭圆C′;同理Cn,Cn+1共焦点且与同一条直线ln相切,故Cn,Cn+1也为同一个椭圆;不难得到,C1,C2,…,Cn+1,…均为椭圆C′;因此所有光线均与同一个椭圆C′相切.此性质类似于包络,故称椭圆C′为“包络”椭圆.对于一般情况,如图7所示,当光线经椭圆不断反射无数多次后,光线将围出一个椭圆(即C′),但因为我们无法证明椭圆C′上的每一点都是光线与C′的切点,故不能严格证明这是一个包络现象.对于更特殊的情况(如图8),光线还会形成回路.
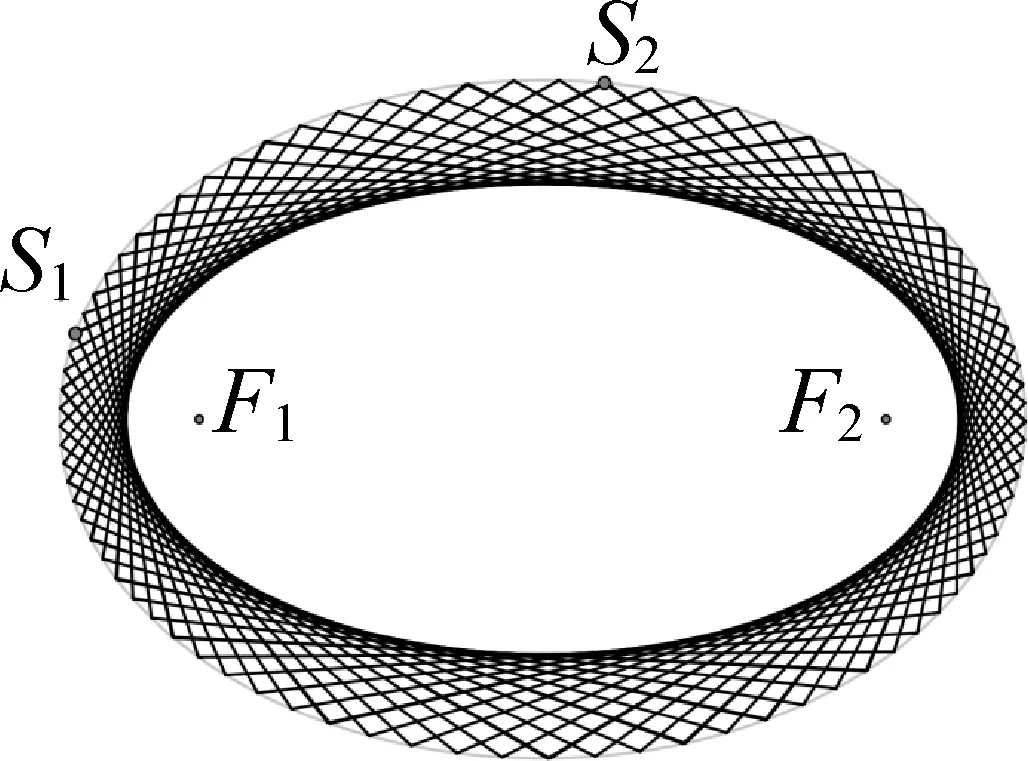
图7

图8
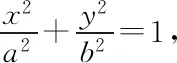
1.3 初始光线与椭圆两焦点连线段相交(交点非端点)时的光学性质
为证明方便,我们先介绍双曲线焦点弦的光学性质.
引理4点P在以F1、F2为焦点的双曲线上,从F2射出的光线经过P点双曲线反射后的反射光线与从F1点射出经过P点的光线在同一条直线上.
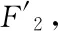
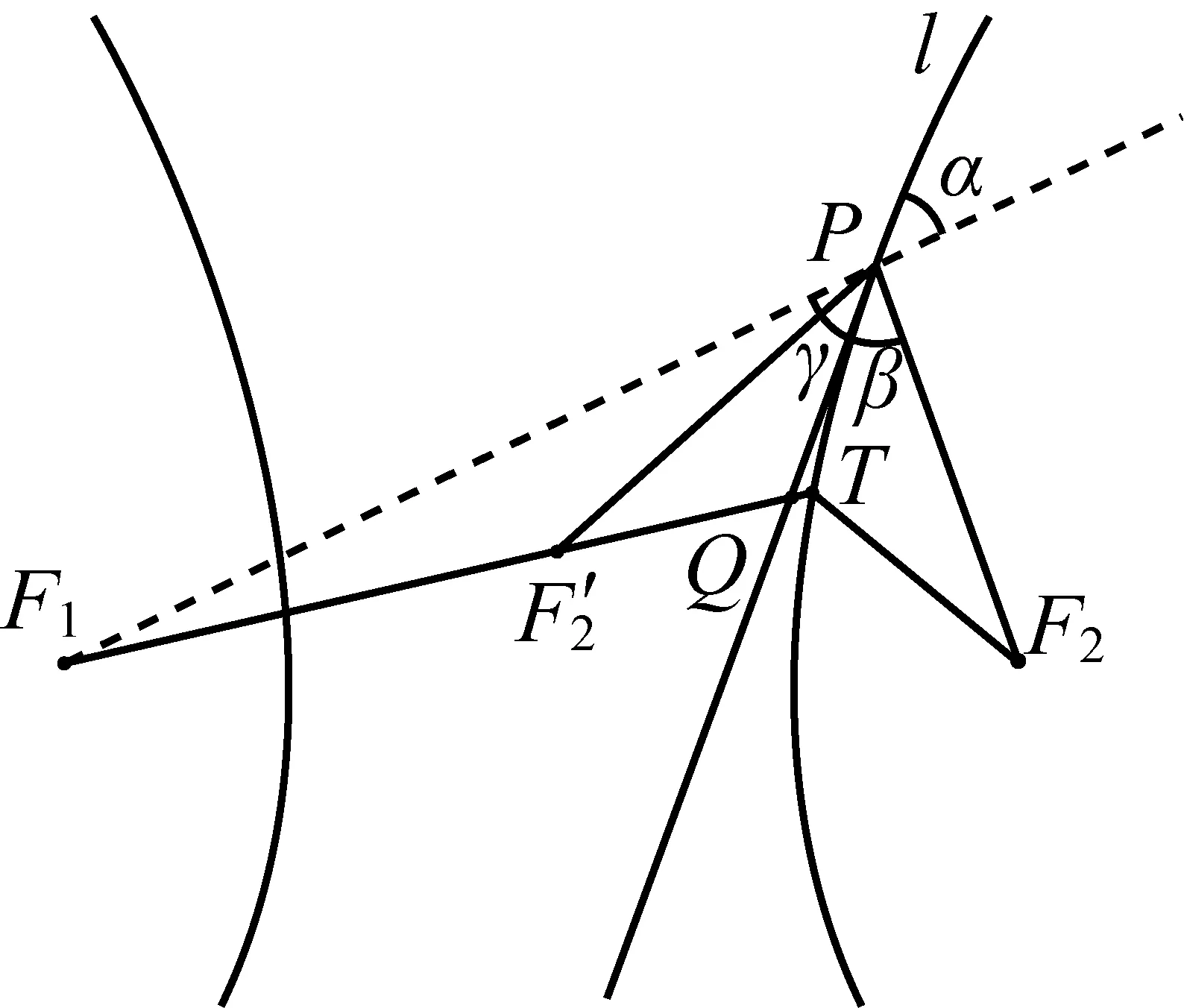
图9
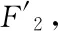
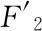
至此我们便可以讨论初始光线与椭圆两焦点连线段相交时的光学性质了.
定理2如图10,椭圆C以F1、F2为两焦点,椭圆C的弦S1S2与线段F1F2相交(交点异于F1、F2),从S1发出的光线S1S2经椭圆反射后反射光线为S2S3,则入射光线S1S2和反射光线S2S3所在直线均与一个以F1、F2为焦点的双曲线C′相切.

图10
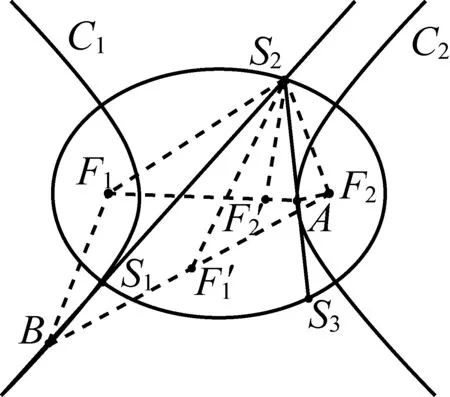
图11
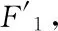
于是可知,设椭圆C0内部初始光线所在直线为l0,经椭圆C0反射n次后的反射光线所在直线为ln.当l0与椭圆C0焦点连线段相交(交点非端点)时,由定理2得,可设l0与l1同与双曲线C1相切、l1与l2同与双曲线C2相切,…,ln与ln+1同与双曲线Cn+1相切…;其中C1、C2,…,Cn+1,…均与C0同焦点.因此C1,C2共焦点且与同一条直线l1相切,故C1,C2为同一个双曲线,记作双曲线C′;同理Cn,Cn+1共焦点且与同一条直线ln相切,故Cn,Cn+1也为同一个双曲线;不难得到,C1,C2,…,Cn+1,…均为双曲线C′;因此所有光线均与同一个双曲线C′相切.与之前结论一样,这是一个类似于包络的现象(我们无法严格证明),故称双曲线C′为“包络”双曲线,对于一般情况,如图12所示,当光线经椭圆不断反射无数多次后,光线将围出一个双曲线(即C′).
图12
2 抛物线中相应的结论与证明
参考椭圆中的不同情况,在抛物线中也对初始光线的位置分三种情况讨论.
第一种情况:当光线经过抛物线焦点时,相关结论已广为人知,下面给出一种证明.
定理3抛物线C以A为焦点,l为准线,点P为抛物线C上一点,从点A射出的光线经过点P处抛物线反射后的反射光线与l垂直.
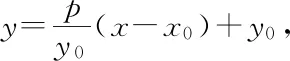
在讨论第二种情况前,先证如下引理:
引理6如图13,在定理3中作点A关于点P处抛物线切线的对称点A′,则A′在准线l上,且A′P⊥l.

图13
证明过点P作准线l的垂线,垂足为点A″,由抛物线定义知|A″P|=|AP|,又由定理3知∠A″PT=∠γ=∠α,故可得点A″与点A′重合,故引理成立.
第二种情况:过抛物线焦点作准线的垂线段,当初始光线与该垂线段相交时,有如下光学性质:
定理4过抛物线C1的焦点F作准线l1的垂线段,抛物线弦S1S2与该垂线段相交,从S1发出的光线S1S2经抛物线反射后反射光线为S2S3,则入射光线S1S2与反射光线S2S3均与另一个以F为焦点,准线与l1平行的抛物线C2相切.
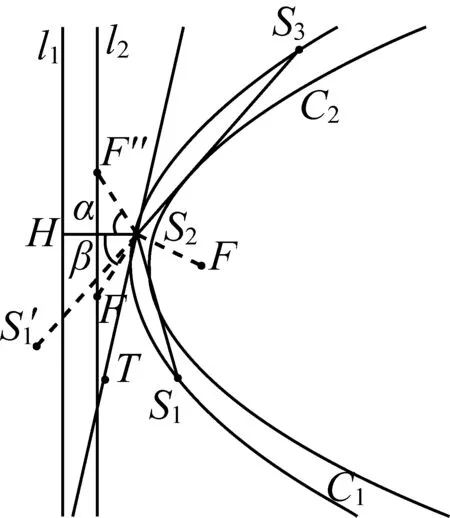
图14
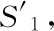
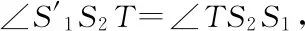
对于第三种情况:过抛物线焦点作准线的垂线段,当初始光线与该垂线段不相交时,得到如图15所示的现象,无法得到良好的性质.
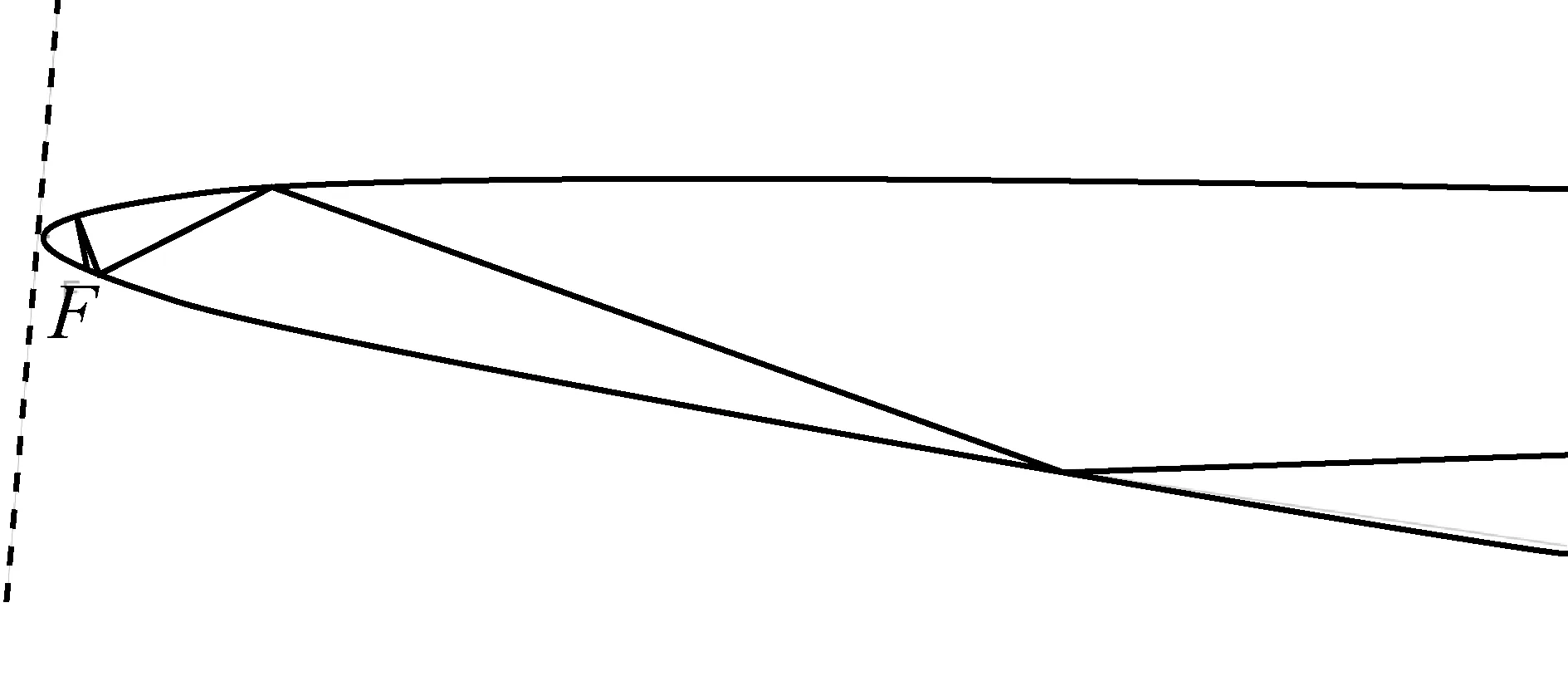
图15
3 结语
通过探究我们发现,光线经双曲线反射后很快发散(如图16、图17所示),因此未能找到良好的性质.在椭圆中我们还企图通过解析法对反射之后的坐标与方程进行研究,以观察能否找到一些规律,以确定哪些特殊情况能够使反射光线形成回路;很遗憾,通过Mathematica的计算结果来看,一次反射之后的坐标与方程已经过于复杂,难以找出规律,希望能通过后续的研究取得一些新的进展.此外,对椭圆中光线能否形成包络现象?如果能够形成包络现象的话对初始光线有何限制条件?等问题都有待进一步的探究.
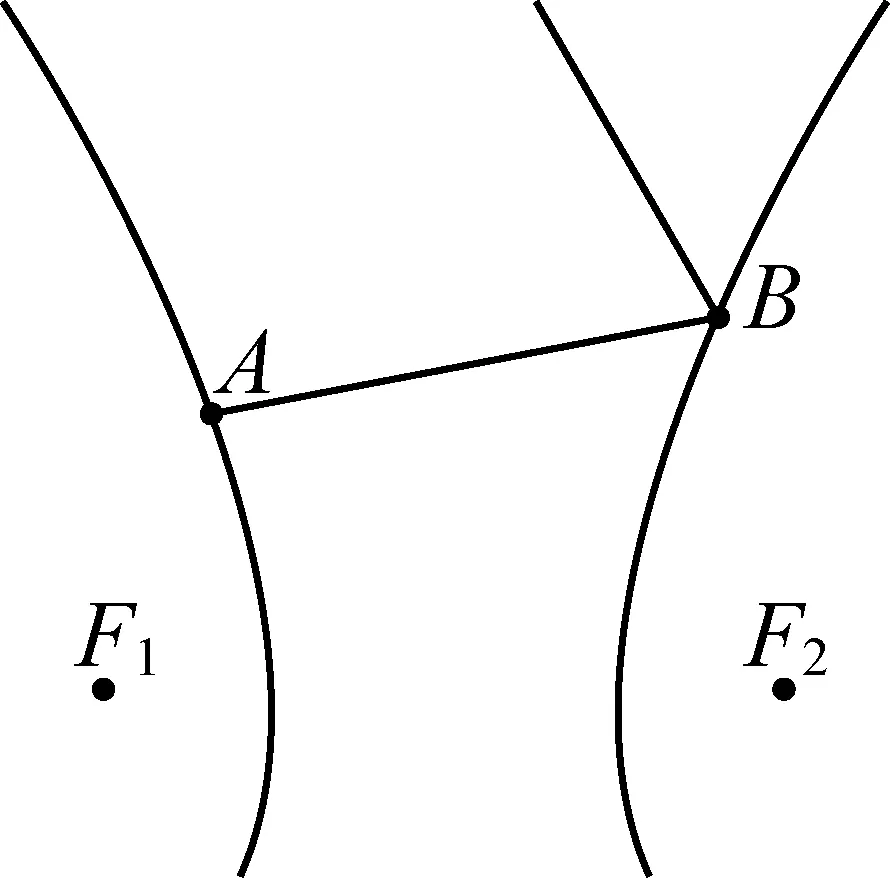
图16
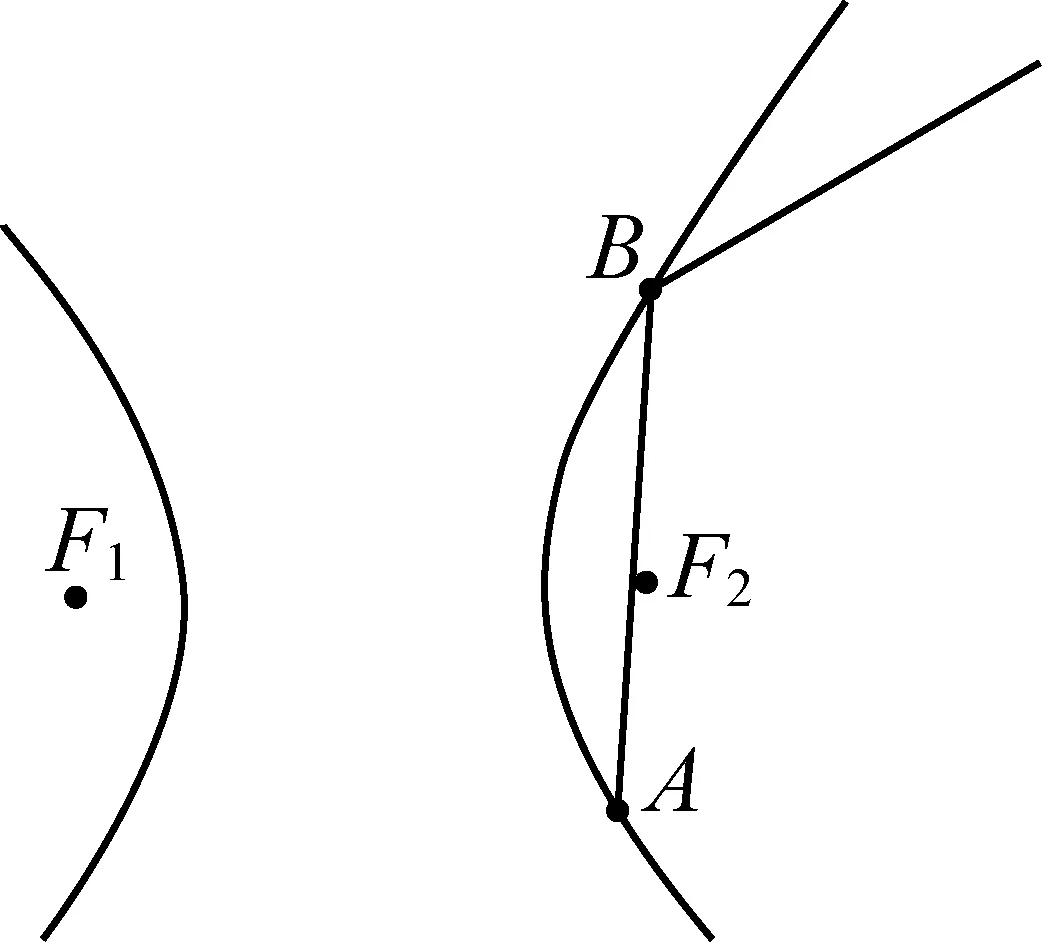
图17

