数学学习的“破”与“立”?
左雷?

【关 键词 】《认 识三 角形 》;先破 后立 ;理性 认识 ;深度 学习
学习 苏教 版四 下《认 识三 角形 》之前 ,学生 在生活中都接触过一些表面呈三角形的物体,大多数学生都知道三角形有三个顶点、三条边、三个角,知道三角形有高矮,能画出三角形。因此,本节课的教学重点,是利用学生的原有认知,把学生对三角形外形的感性认识抽象成理性概念;引导学生理性认识三角形的高,并将三角形的高从生活中高矮的概念里剥离出来,感受生活物体的高矮与三角形的高的异同点;引导学生学会画高。更重要的是,通过观察、操作、比较等具体的活动,培养学生初步的分析、抽象、概括等能力,为今后继续学习和探索多边形的相关知识打下良好的基础。基于上述认识,笔者以移动的磁点为载体,以磁点的位置变化为主线,以“先破后立”为立足点,引出数学问题,引发学生进行数学思考,促进他们开展深度学习。
一、认识三角形
1.基于经验,画三角形。
师( 用三 个磁 点在 黑板 上摆 出三 角形 ):看着这三个点,你能想象出什么平面图形?(三角形)试着在空中比划一下你看到的三角形。今天这节课,我们就来认识三角形。(板书课题)
师:给你这样三个点,你能画出一个三角形吗?(学生在学习单上尝试画三角形)
引导学生从抽象的三个点想象三角形入手,再现已经形成的三角形表象,然后让他们动手画出具象的三角形,将头脑中三角形的表象外显出来,为下面认识三角形的特征做铺垫。
2.基于活动,认识三角形的特征。
师(展示学生画的两幅三角形作品):观察这两幅作品,结合刚才画三角形的经验,想一想,画三角形时要注意什么?
生1:要画直的。(板书:直的)
生2:要把这三个点连起来。(板书:连起来)
生3:画的时候不能超过那个点。
师:你的意思是不能“过了”(用手比划),对吗?(板书:不能过了)如果请你介绍这个三角形,你准备怎么介绍?
生3:三角形有三个顶点、三个角、三条边。引导学生通过观察、操作、比较进一步认识三角形的基本特征,积累认识图形的经验,为接下来抽象三角形的概念做准备。
3.基于积累,建构三角形的概念。
师:说到三角形的三条边,老师突然想到一个问题。(动画演示将三角形三条边分开)你们看,三角形的每条边各有两个端点,三条边就有六个端点,为什么三角形只有三个顶点呢?请把你的想法记在学习单上,记好后再跟同桌交流。
教师巡视,收集作品,然后多媒体展示学生作品。有的写道:有顶点重合了,所以只能看到三个;有的写道:因为有一些顶点重复了;有的写道:有三个端点重叠了。
师:几位同学表述不同,有相通的地方吗?
生:“重合”“重复”“重叠”意思差不多。
师:“重合”是什么意思?谁跟谁重合了?
生:重合就是两个点合在一起了,这条线段的一个端点和另一条线段的一个端点重合了。
师:如果咱们把端点排排序,(做手势)从这开始到这结束,另一条又从这开始往这结束,开始的这个点叫“首”的话,那结束的这个点就叫?(尾)这样的情况就叫?(首尾相接)(板书:由三条线段首尾相接围成的图形叫三角形)
师:回顾刚才大家画三角形时提出的注意点,概念中有没有指出三角形的边是“直的”?
生:有“,线段”就是直的。
师:有没有强调“连起来”呢?(首尾相接)哪个词说的是不能“过了”?(围成)
通过将三角形拆解成三条线段,由线段端点数量与三角形顶点数量不一致引发学生的认知 冲突 ,从而 激发 他们 自主 建构“首 尾相 接”的概念。同时,通过与之前画三角形时总结的注意点相比较,使学生深刻理解概念的内涵,达到“破”感性、“立”理性的教学目标。
4.基于练习,强化概念。让学生在正例与反例辨析的过程中进一步明晰三角形概念的内涵与外延,掌握三角形的基本特征。
5.基于操作,理解顶点间的位置关系。
师:继续观察这三个磁点,如果把这个点摆在这儿(向上或向下移动最上面的顶点,保证三点不在一条直线上),现在还能看出这是三角形吗?(能)现在呢?(可以)摆在这儿呢?(可以)
师:看来这个点很自由。像这样移动下去,可以摆出多少个不同的三角形呢?
生(思考后):无数个。
师:那摆在这儿行吗?(移动磁点,让三个点在一条直线上)(不行)摆在这儿呢?(也不行)
师:这个点好像也没那么自由,它到底放哪儿行,放哪儿不行呢?
生:三个点不能摆在一条直线上。
师:为什么三个点不能摆在一条直线上呢?
生1:三角形得有三个角,这样摆就没有三个角了。
生2:如果三个顶点摆在一条直线上,连接三个点就没有高度了,只能画出一条直线。
教师继续运用可移动的磁点来代替三角形的三个顶点,并引导学生在移动磁点的过程中感 受三 角形 三个 顶点 的“自 由”和“约 束”,体会“无限”和“受限”,从而“破”表象、“立”本质。
二、认识三角形的高
1.感知三角形的高矮。
师(指着三个磁点):回到刚才这个三角形,记住它的样子。(不断向上移动上面的磁点)这个三角形跟刚才比,有什么变化?(变高了)现在呢?(又变高了,继而向下移动这个磁点)现在呢?(变矮了)看来三角形也是有高矮的。
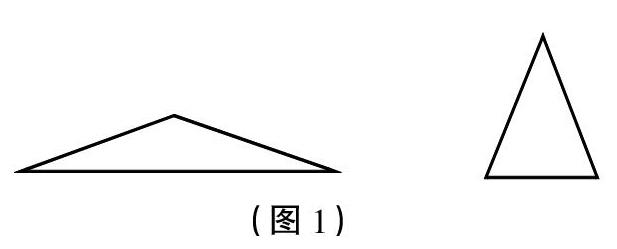
2.研究三角形的高。(1)比高矮。课件出示下页图1。
师:你觉得这两个三角形,哪个高?
生:第二个三角形高。
师:怎么证明?两个三角形究竟有多高?
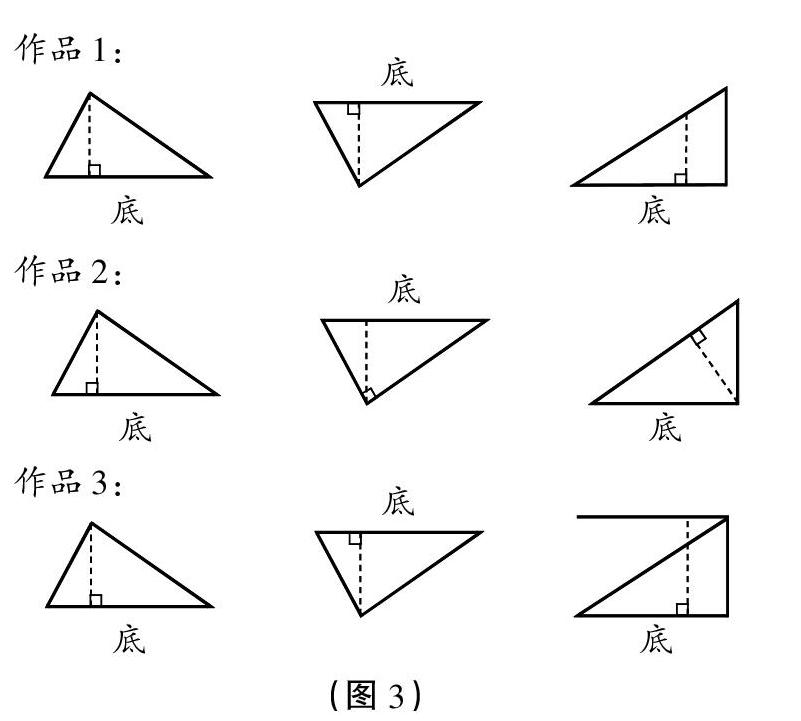
学生自主画高,教师巡视,然后展示如图2 所示的作品1~3。
师:你们觉得哪个作品表达得更准确?
生1:首先可以排除作品1,因为实线就表示将这个三角形分成两部分了,这里用虚线更合适,虚线表示这条线是后画的。
生2:作品3 更准确,他画的是虚线,而且標了直角标记,说明画的是垂线。
师:都是虚线,为什么画垂线更准确呢?
............
师:是的,三角形的高就是从顶点到对边的垂直线段。
(2)教学画高。教师演示画高,强调注意点。
(3)练习画高。学生独立完成练习,教师找生成并有序展示如图3 所示的作品1~3。
师:观察这三个作品,大家有什么想说的?
生1:作品1 第三个三角形的高画错了,应该从顶点向对边画垂直线段。
生2:作品2 第二个高的垂直标记标错了,应该标在底上,因为这是表示与底垂直的线段。
生3 :作品 2第 三个 三角 形的 高画 错了 。他画的是斜边上的高。
师:看来三角形的高和底是有讲究的,它们是“对应”的。作品3 第三个图形中画的是高吗?
生:不是,这条线段不是从顶点到对边的垂直线段。
师:这条线段与高有什么关系呢?生:因为平行线间的垂直线段的长度都相等,所以这条线段的长度和三角形的高相等。
师:三角形的高与生活中的高矮一样吗?
生:不一样,高矮只是指长度,三角形的高是顶点到对边的垂直线段。
师:听明白了吗?看来,三角形的高不只包含长度。大家对三角形高的感觉越来越好了!
借助学生“比高矮”的生活经验,帮助他们初步建立三角形高的概念;接着,让学生在对比中感知生活中的高矮与三角形的高的差异;进而将三角形的高从生活中高矮的概念中剥离出来,达到“破”经验认知、“立”概念实质的目的。
很多时候,学习就是学生不断打破原有认知,逐步重建新的认知的过程。
(作者单位:南京市金陵汇文学校小学部)

