连续自然数及乘积的尾数和奇偶性的分析
曹振民,霍心蕊
(中国路桥工程有限责任公司;中交基础设施养护集团有限公司,北京100011)
概述
在数论研究中,我们经常需要了解一组有一定规律(如连续自然数)的数字中各种奇偶数和尾数的分布情况,如设集合X 和Y 为X={x|x=[x1,x2]}(x1,x2∈N,x2≥x1),Y={y|y=[y1,y2]},(y1,y2∈N,y2≥y1),其 中[x1,x2]表示从x1到x2的连续自然数,[y1,y2]同理。在X 和Y 之间建立一个的二元关系——一般意义上的相乘关系,设它们的乘积为S={(x,y)|x∈X,y∈Y,x*y}。显然X、Y 和S 均为有限集。本文将对集合X、Y 及它们的乘积S 中的数字的奇偶性和尾数分布情况进行分析。
1 定义
为减少歧义,首先给出一些相关定义和分析过程中用到的符号。
1.1 尾数:对于任意给定的整数x,把x 的最后一位数,称为x 的尾数,用符号Ri(x)(x∈Z)表示。如Ri(167)=7,Ri(0)=0,Ri(299)=9.
1.2 余数:对于任意给定的整数x 和d,用符号Mod(x,d)(x,d∈N+)表示x 除以d 的余数。如Mod(5,3)=2,Mod(4,2)=0,Mod(995,233)=63.
2 尾数分析
2.1 集合X 情况
先分析一组连续自然数中尾数个数的计算公式。
定律1:对于给定的集合X=[x1,x2],(x1,x2∈N,x2≥x1),其中尾数为i 的个数为:

式(1)中:Nx(i)——X 中尾数为i 的个数,i∈U,其中U={0,1,2,3,4,5,6,7,8,9}
N0——参数,取值
T(i)——参数,当i=U0时T(i)=0;i=U1时T(i)=1
U1——集合U1={Ri({X1})}⊆U,其中集合X1=[x1,(x2-10N0)]⊆X
U0——U1关于U 的补集,U0=∁UU1
证明:一般地,连续自然数的尾数都是每10 个为一个周期循环。对于给定的集合X=[x1,x2],不妨把它分成两部分,一部分是尾数包含了集合U中所有元素的集合X0,它的基数是10 的整倍数;另一部分是X0关于X 的补集,X1=∁XX0。它的基数为|X1|=|X|-|X0|.显然有X1∪X0=X,X1∩X0=φ(空集).
设Dx=x2-x1,X1和X0的元素在x1~x2之间的分界点为x12,即X1=[x1,x12],X0=[x12+1,x2]。x12的几何意义见图1所示。

图1X拆分示意图
|X1|=x12-x1+1=(x2-10*N0)-x1+1=Dx-10*N0+1,|X0|=x2-(x12+1)+1=x2-x2+10*N0=10*N0
|X1|+|X0|=Dx-10*NO+1+10*N0=Dx+1=x2-x1+1=|X|,集合X0包含了N0个尾数分别为i(i∈U)的元素;集合X1包含了1个尾数分别为R(x1)~R(x12)的元素,设U1={Ri({X1})},则集合X中尾数为i的个数为上述两者之和。证毕!
举例1:求(22~2798)之间尾数为0~9的个数。
解:设X=[22,2798],x1=22,x2=2798,则Dx=x2-x1=
x12=x2-10*N0=2798-2770=28,X1=[x1,x12]={22,23,24,25,26,27,28},|X1|=Dx-10*N0+1=2776-10*277+1=7,X0=[x12+1,x2]=[29,2798],|X0|=10*N0=2770,U1=[Ri({X1})]={2,3,4,5,6,7,8},
U0=∁UU1={0,1,9},从而,X的尾数个数为:

2.2 集合S=X·Y情况
现在讨论两组连续自然数乘积的各种尾数的计算公式及所占比例。
定律2:对于给定的集合X=[x1,x2],(x1,x2∈N,x2≥x1),Y=[y1,y2],(y1,y2∈N,y2≥y1),它 们 的 乘 积S={(x,y)|x∈X,y∈Y,x*y},则S中尾数为k的个数为:

式(3)中,U(k)——集合系列,具体为:

U(1)={(1,1),(3,7),(7,3),(9,9)}
U(2)={(1,2),(2,1),(2,6),(3,4),(4,3),(4,8),(6,2),(6,7),(7,6),(8,4),(8,9),(9,8)}
U(3)={(1,3),(3,1),(7,9),(9,7)}
U(4)={(1,4),(2,2),(2,7),(3,8),(4,1),(4,6),(6,4),(6,9),(7,2),(8,3),(8,8),(9,6)}
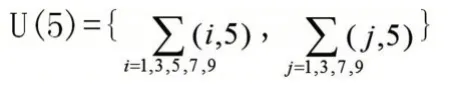
U(6)={(1,6),(2,3),(2,8),(3,2),(4,4),(4,9),(6,1),(6,6),(7,8),(8,2),(8,7),(9,4)}
U(7)={(1,7),(3,9),(7,1),(9,3)}
U(8)={(1,8),(2,4),(2,9),(3,6),(4,2),(4,7),(6,3),(6,8),(7,4),(8,1),(8,6),(9,2)}
U(9)={(1,9),(3,3),(7,7),(9,1)}
Ns(k)——S 中尾数为k 的个数(k∈U,U={0,1,2,3,4,5,6,7,8,9})
Nx(i)——X 中尾数为i 的个数(i∈U),可由(1)式求出.
Ny(j)——Y 中尾数为j 的个数(j∈U),可由(1)式求出.
证明:对于给定的集合X 和Y 的乘积S,其各种尾数的个数由X 和Y 的尾数个数确定,而X 和Y 的尾数可由定律1求出。
如S 中尾数为1的个数,只有Ri({X})中1,3,7,9与Ri({Y})中的1,7,3,9 分别相乘后得出,即Ns(1)=Nx(1)*Ny(1)+Nx(3)*Ny(7)+Nx(7)*Ny(3)+Nx(9)*Ny(9)。S中尾数为9的个数,只能由集合X和Y中的(1*9),(3*3),(7*7),(9*1)得出,简写为:
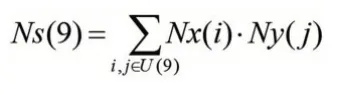
其中U(9)={(1,9),(3,3),(7,7),(9,1)}。其余尾数个数的计算方法同理。证毕!
举例2:求(22~2798)与(197~981)的乘积中,尾数分别为0~9的数字的个数。
解:设X=[22,2798],Y=[197,981],计算过程见表1和表2。

表1基本参数计算
现举例说明表2中尾数为3的计算过程,其余尾 数计算过程同理。
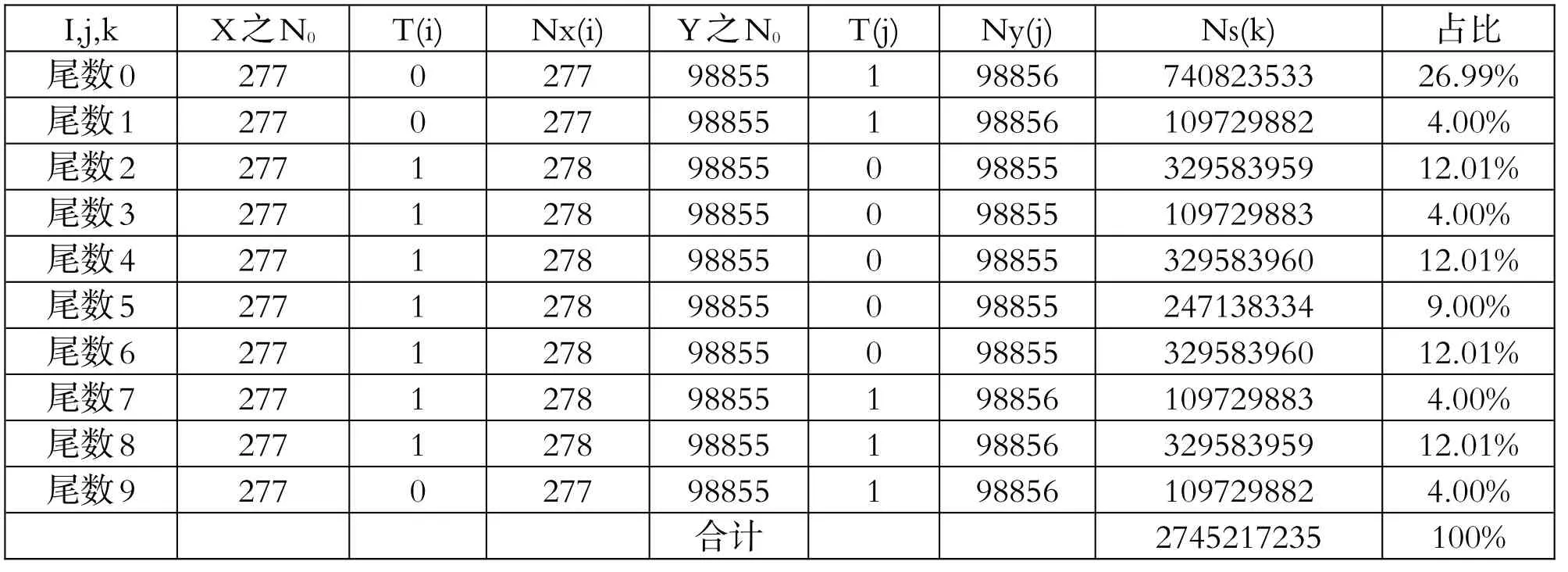
表2 计算结果
据(3)式,Ns(3)=Nx(1)·Ny(3)+Nx(3)·Ny(1)+Nx(7)·Ny(9)+Nx(9)·Ny(7)=109729883
由表2 可看出,尾数为奇数1,3,7,9 的数字约占比4%,尾数为奇数5 的数字约占比9%,尾数为0 的数字约占比27%,尾数为偶数2,4,6,8 的数字的占比均为12%。偶数(含0)总的占比为:

这是一个有趣的现象。我们在下面进行奇偶性分析时还会提到这一点,并给出证明。
3 奇偶性的分析
3.1 集合X情况
先给出一组连续自然数中奇偶数个数的计算公式。
定律3:对于给定的集合X=[x1,x2],(x1,x2∈N,x2≥x1),基数为|X|=x2-x1+1,设其奇数的个数为No,偶数的个数Ne,则有:
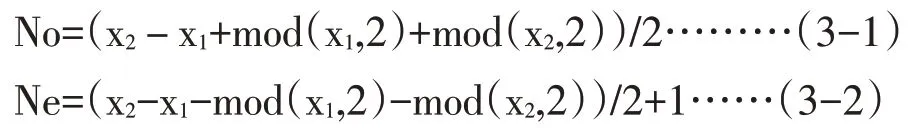
在此,我们姑且认为尾数为0的数字属于偶数。
在进行检验标本采集的过程中,检验工作者必须要充分了解患者的身体状况以及需要检查的项目,并告知患者在标本采集之前应当特别注意的地方,如:在采取样本之前,根据其需要检查的项目来嘱咐患者合理饮食、合理运动、尽量不服用药物等,以确保采取样本的可靠性,从而保障检验结果的准确性。
证明:连续自然数的奇数个偶数是间隔分布的,奇数和偶数的个数基本相同,大约各占一半,两者的差别仅在于给出的x1和x2的奇偶情况。现由取余函数mod 来确定x1和x2的奇偶性,由于mod(x,2)=0 时则x 为偶数,mod(x,2)=1时则x 为奇数,而x1、x2的奇偶性不外乎4种情况:
(1)x1为奇x2为奇:即mod(x1,2)=mod(x2,2)=1,显然x2-x1为偶数
则No=(x2-x1)/2+1=(x2-x1)/2+1/2+1/2=(x2-x1)/2+(mod(x1,2)+mod(x2,2))/2
(2)x1为奇x2为偶:即mod(x1,2)=1,mod(x2,2)=0,显然x2-x1为奇数
则No=(x2-x1)/2+0.5=(x2-x1)/2+1/2+0/2=(x2-x1)/2+(mod(x1,2)+mod(x2,2))/2
(3)x1为偶x2为奇:即mod(x1,2)=0,mod(x2,2)=1,显然x2-x1为奇数
则No=(x2-x1)/2+0.5=(x2-x1)/2+0/2+1/2=(x2-x1)/2+(mod(x1,2)+mod(x2,2))/2
则No=(x2-x1)/2+0=(x2-x1)/2+0/2+0/2=(x2-x1)/2+(mod(x1,2)+mod(x2,2))/2
而Ne=(x2-x1+1)-No=(x2-x1-mod(x1,2)-mod(x2,2))/2+1,证毕!
3.2 集合X·Y情况
定律4:对于给定的集合X=[x1,x2],(x1,x2∈N,x2≥x1),Y=[y1,y2],(y1,y2∈N,y2≥y1),它们的乘积S={(x,y)|x∈X,y∈Y,x*y},则S 中奇数个数Nso 和偶数个数Nse可由下式求出:
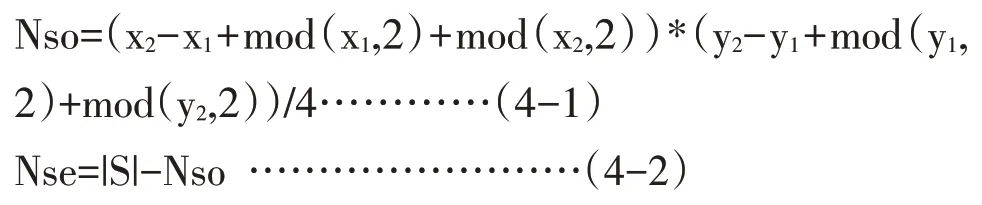
在此,我们姑且认为尾数为0的数字属于偶数。
证明:设集合X 和Y 中的奇数分别为Nxo 和Nyo,偶数分别为Nxe 和Nye,它们可以由上述的(3-1)和(3-2)式求出。由于偶*偶=偶*奇=奇*偶=偶,而奇*奇=奇,所以S 中的奇数只能由X 和Y 中的奇数相乘得出,即:No=Nxo·Nyo=(x2-x1+mod(x1,2)+mod(x2,2))·(y2-y1+mod(y1,2)+mod(y2,2))/4
Ne=(Nxo+Nxe)·(Nyo+Nye)-Nxo·Nyo=|X|·|Y|-Nso=|S|-Nso ,证毕!
举例3:求(22~2798)与(197~988751)乘积中,奇数和偶数的数字的个数。
解:根据公式(3-1)得,奇数Nso=
=(2798- 22 + mod(22,2)+ mod(2798,2))*(988751-197+mod(197,2)+mod(988751,2))/4
=(2776+0+0)(988554+1+1)/4=2776*988556/4=686057864
偶数Nse=(2798-22+1)·(988751-197+1)-Nso=2777*988555-686057864=2059159371
奇数占比686057864/2745217235=24.99%.
实际上,在两组连续的自然数(x1~x2)和(y1~y2)的乘积中,当乘积的数据充分多时,奇数占比趋向于25%,偶数占比趋向于75%。证明如下:
根据公式(4),设mx=(mod(x1,2)+mod(x2,2)),my=(mod(y1,2)+mod(y2,2)),
dx=x2-x1,dy=y2-y1,可求得:Nso=(dx+mx)*(dy+my)/4,
则奇数占比γO=Nso/Nxy=(dx+mx)*(dy+my)/[(dx+1)*(dy+1)]/4
mx和my为一常数,两者之和最大为2,最小为0,所以当dx 或dy 其中的一项充分大时,奇数占比γO为:

这也解释了上述表2中所有奇数的百分比之和(4%+4%+9%+4%+4%)约等于25%的原因。

