处理立体几何客观题的４种思维方式

◇ 山东 刘 英

立体几何是考查学生空间想象能力及推理论证能力的主要题型,通常与立体几何有关的客观题,都是小题,但解题方法灵活,解题中除了要熟练掌握空间点、线、面之间的关系及平面几何图形的有关性质外,还要掌握一些特殊的解题思维,如折叠、展开、分割、补形等．

1 折叠

例1(2020年全国卷Ⅰ)如图1所示,在三棱锥P-ABC的平面展开图中,AC＝AB⊥AD,∠CAE＝ 30°,则cos∠FCB＝__________．

解析知条件得PA,AB⊥AC,∠CAP＝30°,故求cos∠FCB,即求cos∠PCB．

将平面图形折叠成三棱锥(如图2所示),由已

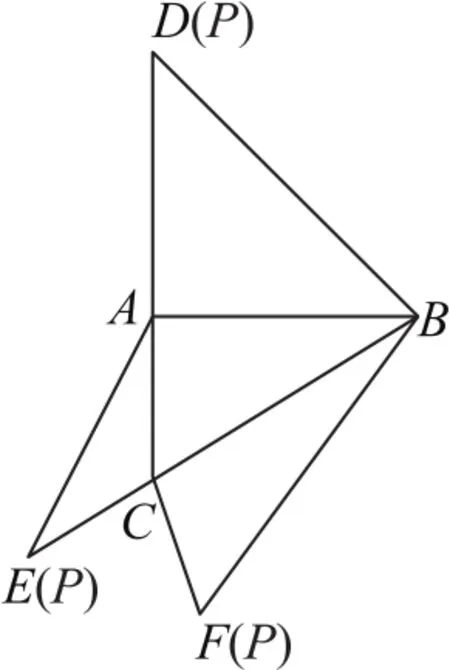
图1

在△PAC中,AC＝1,,由余弦定理得PC2＝3＋1－,所以PC＝1．

图2

在Rt△ABC中,AB＝,则BC＝2．同理在Rt△PAB中,有PB＝．所以在△PBC中,由余弦定理得cos∠PCB＝

解析

本题给出了三棱锥的平面展开图,可按要求将其折叠成空间几何体,再结合已知条件求解．应用此类思维方式解题时要注意平面展开图与立体图形中点、线、面的对应关系．

2 展开

例2如图3所示,P是圆锥的顶点,O是底面的圆心,AB为直径,点C是圆O上异于A,B的点,且PO＝OB＝1,,点E在线段PB上,则CE＋OE的最小值为________．

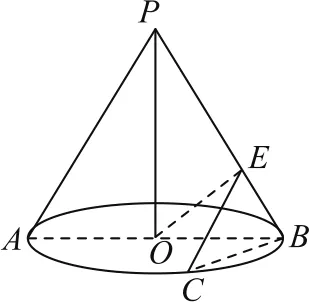
图3

解析

在△POB中,PO＝所以．连接PC,同理可得．所以在△PBC中,PB＝

在三棱锥P-ABC中,将侧面PCB绕PB旋转至平面PBC′的位置,使其与平面PAB共面,如图4所示．当点O,E,C′共线时,CE＋OE的值最小．

图4

在△OC′P中,由余弦定理得

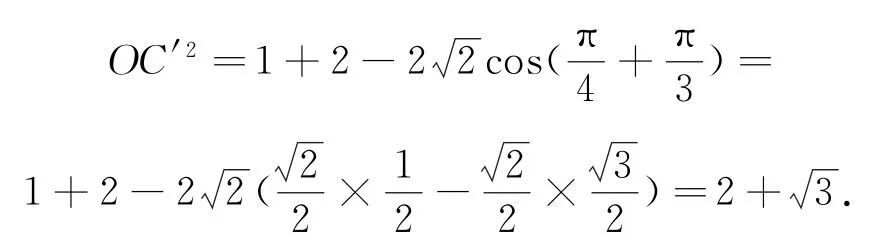
点评

空间问题平面化是解答立体几何问题的重要思维方式,特别是在处理空间几何体表面上动点到两定点间距离之和最小时,将空间中的面展开,则可将问题转化为平面内动点到两定点距离之和最小问题．

3 分割

例3如图5所示,在棱长为1的正方体ABCD-A1B1C1D1中,E是棱CC1上的一个动点,平面BED1交棱AA1于点F,则四棱锥B1-BED1F的体积为( )．

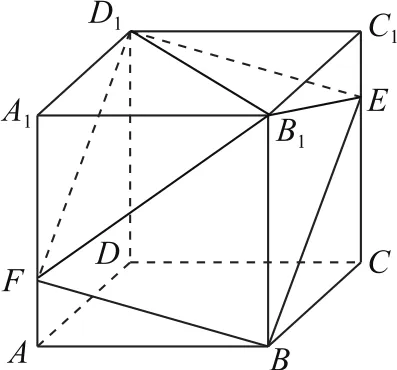
图5

解析

如图6所示,连接BD1,则可将四棱锥B1-BED1F分割成两个三棱锥D1-BFB1,D1-BB1E．设h1为D1到平面BFB1的距离,h2为D1到平面BB1E的距离,则

所以四棱锥B1-BED1F的体积为．故选B．

点评

本题若直接求四棱锥B1-BED1F的体积,其底面积和高都不易求得,通过分割法将不规则几何体转化为规则几何体,计算方便,从而快速求得结论．

图6

4 补形

例4如图7所示,在三棱锥P-ABC中,PA⊥,PA和BC的公垂线ED交PA于点E,交BC于点D,ED＝3,则三棱锥P-ABC的体积为( )．

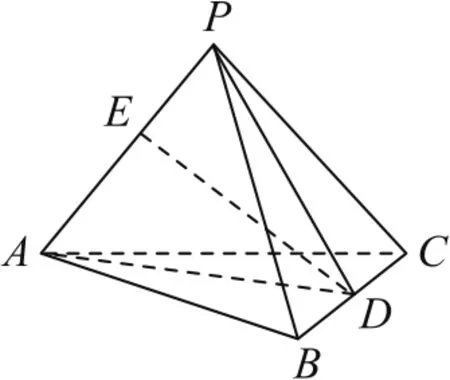
图7

解析

如图8所示,以△ABC为底面,PA为侧棱,将三棱锥P-ABC补为三棱柱PB1C1-ABC,连接EB,EC．因为PA⊥BC,PA⊥DE,所以PA⊥平面BEC,所以

图8

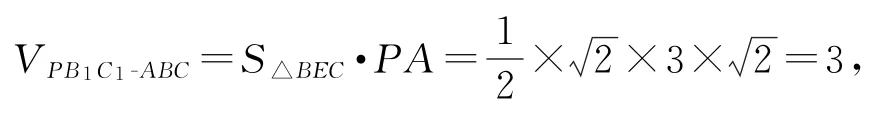
点评

通过补形法,将不规则的几何体构造为特殊的几何体(特殊的几何体一般指长方体、正方体、三棱柱等),从而将其中隐含的几何关系直观地体现出来,即化隐为显,进而准确找到解题的切入点．

综上所述,折叠、展开、分割、补形是处理空间几何问题的重要思维方式,教学中教师要培养学生观察、想象、转化能力,灵活应用各种思维,进而提高学生综合问题的求解能力．