偏序集的软理想

梁世欣，郝旭东

(华东师范大学 哲学系，上海 200241)

0 引 言

偏序集理论的发展时间尚短，关于偏序集理论的专业杂志Order是1984年第一次出版的. 之后，Bernd S.W.Schröder在OrderedSets:Anintroduction中列举了许多公开问题，如代数拓扑方向、序与分析的关系等等. 可见，偏序集作为一种序结构与数学的另外两大结构(代数结构和拓扑结构)有着很大的交叉研究价值[1]. 虽然偏序集理论的发展时间不长，但是作为具有特殊序关系，同时具有序结构和代数结构的格早在19世纪末就被Julius W.R.Dedekind提出来了. 而理想作为格论中一重要概念一直被广大学者所研究. 理想这一概念是由Marshall H. Stone首次提出的，它是建立交换环理论的基础. 之后人们将理想与各种代数理论相结合，研究关于理想的性质. 2006年，姜广浩和王戈平提出了偏序集上的局部极大理想，并研究了它的存在性以及偏序集的理想的分解[2]. 之后，姜广浩和徐罗山又给出了偏序集上的滤子极大理想的定义，证明了其相应的存在性定理[3]； 2008年，潘美林受文献《偏序集上的局部极大理想》的启发，给出了偏序集的弱理想和弱滤子的概念，研究了它们的一些性质.[4]随后，姜广浩等先后给出了偏序集上滤子极大理想的若干注记和偏序集上的理想极大滤子及其应用，并对其性质进行了考察[5-6].

对于软集理论的研究可以回顾到1999年，在俄罗斯数学家D.Molodtsov看来，经典的概率论、模糊集理论和区间数学方法作为处理不确定性的数学工具，都具有各种典型的不确定性的困难[7]. 为了更好地解决社会科学、医学、工程学和环境学等方面的复杂问题，软集理论作为一种处理不确定性的、模糊性的或者是没有明确定义的对象的普遍适用的数学工具被D.Molodtsov首次提出. 之后印度数学家P. K. Maji等人在2003年做了大量的补充工作，给出了软集的一些代数运算，如并、交运算以及且、或运算，并给出了一些相关性质[8]. H. Aktas等随后将软集与模糊集和粗糙集等相关概念进行了比较，然后给出了软群的概念，并且刻画了它的相关性质，由此开创了软集代数研究的新方向[9]. 在软集代数方面，F. Feng等在2008年将软集理论运用到半环中，提出了软半环和软半环的软理想等代数结构[10]. 同年，Y. B. Jun等提出了软BCI/BCK(子)的新的代数结构，并研究了其相关性质[11]. 之后，付文清等研究了软BCK代数并给出软BCK-代数的广义交和广义并运算[12]. 软环的定义也于2010年由U. Acar等给出，他们对软环的软理想和软同态等相关性质进行了研究[13]. 廖祖华等在2012年引入并研究了软坡及其相关性质[14-15]. 之后，还有众多学者对软集代数理论及其应用方面进行了一系列的研究[16-18].

文献《软BCI-代数的软a-理想》将软集与BCI-代数的理想相结合，提出了软BCI-代数的软a-理想的新的结构[19]. 本文受此启发，按照通常国际上软集代数的定义方式，将软集理论与序理论相结合，给出了偏序集的软理想等概念，运用点态化的证明方法证明其上的运算的性质，丰富了软集代数方面的理论. 本文在第二部分中给出文中需要的基本概念和相关定理，第三部分给出了偏序集的软理想的概念，给出了软理想在软集不同运算下的性质，第四部分引入了偏序软同构的概念，获得了在偏序软同构下软理想的像的性质.

1 预备知识

定义1.1[20]设P是一个集合，P上的二元关系≤叫作一个偏序关系，如果满足

(1)自反性：a≤a，(∀a∈P)，

(2)反对称性：a≤b，b≤a⟹a=b，(∀a,b∈P)，

(3)传递性：a≤b，b≤c⟹a≤c，(∀a,b,c∈P)，

这时称(P,≤)(或简称P)为一个偏序集.

定义1.2(笛卡儿积)A，B是两个非空集合，记A×B为A，B的笛卡儿积，且A×B={(x,y)|x∈A,y∈B}.

定义1.3[20]设(P,≤)与(Q,≤)是两个偏序集，称映射f:P→Q为序同态，如果满足

(1)x≤y⟹f(x)≤f(y)，(∀x,y∈P)

称f为满序同态，如果f既满足(1)又是满射，称f为序同构，如果f是满射，且满足(1)与

(2)x≤y⟸f(x)≤f(y)，(∀x,y∈P).

定理1.1序同构f:P→Q是双射.

证明要证明f:P→Q是双射，由已知f是满射，故只要证明f是单射即可.

事实上，∀x,y∈P，若f(x)=f(y)，则f(x)≤f(y)且f(x)≥f(y)，由定义1.3得，x≤y且x≥y，因为(P,≤)为偏序集，所以x=y.

注1.1： 定义1.3将文献[10]中的序同构的定义f是双射的条件减弱为满射.

定义1.4[20](直积) 令T=X×Y(笛卡儿积),在T中如下定义一个二元关系≤:(x,y)≤(x′,y′)⟺x≤Xx′且y≤Yy′，(∀(x,y),(x′,y′)∈T). 易见≤是T上的一个偏序关系，称偏序集(T,≤)是偏序集X与偏序集Y的直积，记作T=X×Y或T=XY.

定义1.5[21]设I为偏序集X的一个非空子集，∀x∈X，∀y∈I，若x≤y可以推出x∈I，称I是X的理想.

定理1.2设M，N为偏序集X的理想，则M∪N仍为X的理想.

证明∀x∈X，∀y∈M∪N，若x≤y，又y∈M或y∈N，

(1)当y∈M时，因M是偏序集X的理想，由

x≤y知，x∈M；

(2)当y∈N时，同理可证x∈N；

故x∈M或x∈N，即x∈M∪N，所以它们的并仍为X的理想.

定理1.3设M，N为偏序集X的理想，则M∩N仍为X的理想.

证明∀x∈X，∀y∈M∩N，若x≤y，又y∈M且y∈N，

(1)当y∈M时，因M是偏序集X的理想，由

x≤y知，x∈M；

(2)当y∈N时，同理可证x∈N；

故x∈M且x∈N，即x∈M∩N，所以它们的交仍为X的理想.

定理1.4设M，N分别是偏序集X1，X2的理想，则直积M×N是X1×X2的理想.

证明∀(x,y)∈X1×X2，∀(a,b)∈M×N，若(x,y)≤(a,b)，即x≤a且y≤b. 因M是X1的理想，N是X2的理想，故x∈M且y∈N，所以(x,y)∈M×N，即M×N是X1×X2的理想.

定义1.6[7]设U是一个论域，E是参数集，A⊂E，P(U)是U的幂集，若F是A到P(U)的映射，则称(F,A)为U上的一个软集.

定义1.7[22]设(F,A)和(G,B)分别是U和U′上的软集，定义软集的直积(F,A)×(G,B)如下： (F,A)×(G,B)=(H,C)，其中C=A×B，H(x,y)=F(x)×G(y)，∀(x,y)∈A×B.

定义1.8[8]设(F,A)，(G,B)为U上两个软集，若满足

(1)A⊂B；

(2)∀e∈A，F(e)=G(e).

则称(F,A)为(G,B)的软子集，记为

定义1.9[8]设(F,A)和(G,B)是U上的两个软集，定义它们的扩展并为软集(H,C)，其中C=A∪B，且∀e∈C，

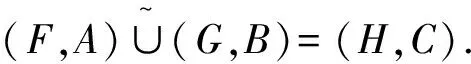
定义1.10[23]设(F,A)和(G,B)是U上的两个软集，定义它们的扩展交为软集(H,C)，其中C=A∪B，且∀e∈C，

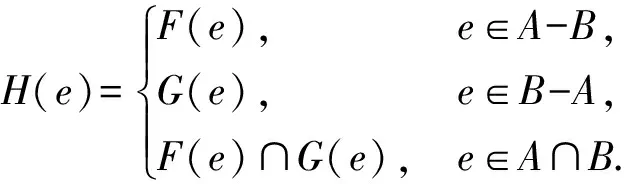
记(F,A)∩E(G,B)=(H,C).

定义1.11[23]设(F,A)和(G,B)是U上的两个软集，且A∩B≠φ，

(1)定义它们的限制交为软集(H,C)，其中C=A∩B，且∀c∈C，H(c)=F(c)∩G(c)，记为(F,A)∩R(G,B)=(H,C)；

(2)定义它们的限制并为软集(H,C)，其中C=A∩B，且∀c∈C，H(c)=F(c)∪G(c)，记为(F,A)∪R(G,B)=(H,C).

(3)定义它们的限制差为软集(H,C)，其中C=A∩B，且∀e∈C，H(e)=F(e)-G(e)，记为(F,A)∩D(G,B)=(H,C).

定义1.12[8]设(F,A)，(G,B)为U上两个软集，令(F,A)∧(G,B)=(H,A×B)，其中H(α,β)=F(α)∩G(β)，∀(α,β)∈A×B，则称(F,A)∧(G,B)为(F,A)和(G,B)的且运算.

定义1.13[8]设(F,A)，(G,B)为U上两个软集，令(F,A)∨(G,B)=(O,A×B)，其中O(α,β)=F(α)∪G(β)，∀(α,β)∈A×B，则称(F,A)∨(G,B)为(F,A)和(G,B)的或运算.

定义1.14[22]设(F,A)和(G,B)分别是U和U′上的软集，f:U→U′，g:A→B是两个映射，则称偶(f,g)是一个(F,A)→(G,B)的软映射，由(f,g):(F,A)→(G,B)表示，如果满足f(F(x))=G(g(x))，∀x∈A. 若f和g是单射(或双射或满射)，那么(f,g)被称为单射(或双射或满射).

2 偏序集的软理想

定义2.1设X是一个偏序集，(F,I)是一个软集，若∀x∈I，F(x)是X的理想，则(F,I)是偏序集X的软理想.

例子2.1设U={a,b,c,d,e,}，则(P(U),⊆)是偏序集，令E={λ1,λ2,λ3,λ4}为参数集，A={λ1,λ2,λ3}，F:A→P(U)，

F(λ1)={φ,{a},{b},{a,b}}，

F(λ2)={φ,{a}},

F(λ3)=

{φ,{a},{b},{c},{a,b},{b,c},{a,c},{a,b,c}}，因F(λ1)，F(λ2)，F(λ3)都是P(U)的理想，则(F,A)为(P(U),⊆)的软理想.

定理2.1设(F,I)是偏序集X的一个软理想，如果C⊆I，那么(F|C,C)是X的一个软理想，其中F|C表示F在C上的限制.

证明∀x∈C⊆I，F|C(x)=F(x)，因(F,I)是X的一个软理想，故F|C(x)=F(x)是X的理想，则(F|C,C)是偏序集X的一个软理想.

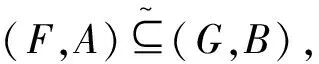
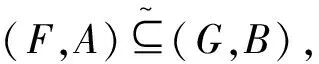
定理2.3设(F1,I1)和(F2,I2)是偏序集X的两个软理想，则它们的扩展并(F1,I1)∪E(F2,I2)也是偏序集X的软理想.

证明令(F1,I1)∪E(F2,I2)=(F,I)，其中I=I1∪I2，且∀x∈I，

(1)当x∈I1-I2时，F(x)=F1(x)，由于(F1,I1)是X的软理想，F1(x)是X的理想，故F(x)是X的理想；

(2)当x∈I2-I1时，同理可证，得F(x)是X的理想；

(3)当x∈I1∩I2时，x∈I1且x∈I2，由已知(F1,I1)和(F2,I2)都是X的软理想，所以F1(x)和F2(x)都是X的理想，由定理1.2得，F1(x)∪F2(x)仍是X的理想； 综合(1)(2)和(3)可得，F(x)是X的理想，故(F,I)是X的软理想.

定理2.4设(F1,I1)和(F2,I2)是偏序集X的两个软理想，则它们的扩展交(F1,I1)∩E(F2,I2)也是偏序集X的软理想.

证明令(F1,I1)∩E(F2,I2)=(G,I)，其中I=I1∩I2，且∀x∈I，

(1)当x∈I1-I2时，G(x)=F1(x)，由于(F1,I1)是X的软理想，F1(x)是X的理想，故G(x)是X的理想；

(2)当x∈I2-I1时，同理可证，故G(x)是X的理想；

(3)当x∈I1∩I2时，x∈I1且x∈I2，由已知(F1,I1)和(F2,I2)都是X的软理想，所以F1(x),F2(x)都是X的理想，由定理1.3得，F1(x)∩F2(x)仍是X的理想；

综合(1)(2)和(3)可得，G(x)是X的理想，故(G,I)是X的软理想.

定理2.5设(F1,I1)和(F2,I2)是偏序集X的两个软理想，且I1∩I2≠φ，则它们的限制并(F1,I1)∪R(F2,I2)也是X的软理想.

证明令(F1,I1)∪R(F2,I2)=(F,I)，其中I=I1∩I2.且∀x∈I=I1∩I2，F(x)=F1(x)∪F2(x)，所以x∈I1且x∈I2，因(F1,I1)和(F2,I2)都是X的软理想，从而F1(x)和F2(x)都是X的理想，由定理1.2得，F1(x)∪F2(x)仍是X的理想，故(F,I)是X的软理想.

定理2.6设(F1,I1)和(F2,I2)是偏序集X的两个软理想，且I1∩I2≠φ，则它们的限制交(F1,I1)∩R(F2,I2)也是X的软理想.

证明令(F1,I1)∩R(F2,I2)=(G,I)，其中I=I1∩I2. ∀x∈I=I1∩I2，G(x)=F1(x)∩F2(x)，所以x∈I1且x∈I2，因(F1,I1)和(F2,I2)都是X的软理想，从而F1(x)和F2(x)都X是的理想，由定理1.3得，F1(x)∩F2(x)是X的理想，故(G,I)是X的软理想.

定理2.7设(F1,I1)和(F2,I2)是偏序集X的两个软理想，且I1∩I2≠φ，若∃x0∈I=I1∩I2，使得F1(x0)∩F2(x0)≠φ，则它们的限制差(F1,I1)∪D(F2,I2)一定不是X的软理想.

证明令(F1,I1)∪D(F2,I2)=(H,I)，其中I=I1∩I2且∀x∈I=I1∩I2，H(x)=F1(x)-F2(x). 由已知，∃y0∈F1(x0)-F2(x0)，∃z0∈F1(x0)∩F2(x0)且z0≤y0，所以z0∉H(x)，因此,H(x)不是X的理想，即(F1,I1)∪D(F2,I2)不是X的软理想.

定理2.8设(F1,I1)和(F2,I2)是偏序集X的两个软理想，且I1∩I2≠φ，若∀x∈I=I1∩I2，使得F1(x)∩F2(x)=φ，则它们的限制差(F1,I1)∪D(F2,I2)是X的软理想.

证明令(F1,I1)∪D(F2,I2)=(H,I)，其中I=I1∩I2且∀x∈I=I1∩I2，H(x)=F1(x)，因(F1,I1)是偏序集X的软理想，则H(x)=F1(x)是X的理想，即(F1,I1)∪D(F2,I2)是X的软理想.

定理2.9设(F1,I1)和(F2,I2)是偏序集X的两个软理想，则它们的且运算(F1,I1)∧(F2,I2)仍为X的软理想.

证明令(F1,I1)∧(F2,I2)=(F,I1×I2)，其中F(α,β)=F1(α)∩F2(β)，∀(α,β)∈I1×I2，因(F1,I1)和(F2,I2)是偏序集X的两个软理想，故F1(α)和F2(β)是X的理想. 由定理1.3得，F1(α)∩F2(β)为X的理想，所以(F,I1×I2)=(F1,I1)∧(F2,I2)为X的软理想.

定理2.10设(F1,I1)和(F2,I2)是偏序集X的两个软理想，则它们的或运算(F1,I1)∨(F2,I2)仍为X的软理想.

证明令(F1,I1)∨(F2,I2)=(G,I1×I2)，其中G(α,β)=F1(α)∪F2(β)，∀(α,β)∈I1×I2，因(F1,I1)和(F2,I2)是偏序集X的两个软理想，故F1(α)和F2(β)是X的理想. 由定理1.2得，F1(α)∪F2(β)为X的理想，所以(G,I1×I2)为X的软理想，即(F1,I1)∨(F2,I2)为X的软理想.

定理2.11设(F1,I1)，(F2,I2)分别是偏序集X1，X2的软理想，则直积(F1,I1)×(F2,I2)是X1×X2的软理想.

证明令(F1,I1)×(F2,I2)=(F,I)，其中I=I1×I2. ∀(x,y)∈I1×I2，F(x)=F1(x)×F2(y). 因(F1,I1)，(F2,I2)分别是偏序集X1，X2的软理想，故F1(x)和F2(y)分别是X1和X2的理想，由定理1.4得，F1(x)×F2(y)是X1×X2的理想，故(F1,I1)×(F2,I2)是X1×X2的软理想.

3 偏序软同构

定义3.1设(F,A)和(G,B)分别是偏序集U和U′上的软集，如果映射f和g满足以下条件

(1)f是U到U′的满序同态；

(2)g是A到B的满射；

(3)∀x∈A，f(F(x))=G(g(x)).

则称(f,g)是一个偏序软同态，用(F,A)～(G,B)表示.

若满足(2)(3)的同时仍满足(4)f是U到U′的序同构，则称(f,g)是一个偏序软同构，用(F,A)≅(G,B)表示.

定理3.1设M是偏序集U的理想，若f是偏序集U到偏序集U′的序同构，则f(M)是U′的理想.

证明∀u′∈U′，∀n′∈f(M)，若u′≤n′，因为f是满射，∃u∈U，使得u′=f(u)，且∃n∈M，n′=f(n)，因f是U到U′的序同构，则由f(u)≤f(n)推出u≤n，又M是U的理想，则u∈M，故f(u)∈f(M)，即u′∈f(M)，故f(M)是U′的理想.

定理3.2设(F,A)和(G,B)分别是偏序集U和U′上的软集，且(F,A)是U的软理想，若(f,g):(F,A)→(G,B)是一个偏序软同构，则(G,B)是U′的软理想.

证明∀y∈B，因(f,g):(F,A)→(G,B)是一个偏序软同构，则∀x∈A，f(F(x))=G(y). 又(F,A)是U的软理想，故F(x)是U的理想. 由定理3.1得，f(F(x))是U′的理想，即G(y)是U′的理想，故(G,B)是U′的软理想.

4 结论

本文给出了偏序集的软理想的概念，并对其上的运算进行研究后得出下面的结论： 偏序集的软理想在C上的限制和它的软子集仍然都是软理想； 两个偏序集的软理想的扩展交(并)和限制交(并)仍然是软理想. 对于两个偏序集的软理想的限制差分情况讨论，当∃x0∈I=I1∩I2，使得F1(x0)∩F2(x0)≠φ时，两个偏序集的软理想的限制差一定不是软理想； 当∀x∈I=I1∩I2，使得F1(x)∩F2(x)=φ时，两个偏序集的软理想的限制差一定是软理想. 两个偏序集的软理想在且、或和直积运算下仍然是软理想； 在偏序软同构下偏序集的软理想的像是软理想. 对上述结论本文给出了理论上的严格的证明, 并适当加以实例说明. 这些成果丰富了偏序集的理想和软集的理论成果. 另外，在本文研究的基础上，可以利用对偶方法研究滤子及其运算和性质，也可以采用将参数集赋予偏序集的代数结构来引进新型的软理想并研究其性质.