演化博弈的鲁棒稳定与镇定
赵 荣, 冯俊娥
(山东大学数学学院,山东济南 250100)
1 引言
博弈论又称对策论,主要研究公式化了的激励结构间的相互作用,是研究具有斗争或竞争性质现象的数学理论和方法.博弈论的思想有着源远流长的历史,可以追溯到两千多年前我国的“齐威王田忌赛马”,一千五百多年前巴比伦犹太教法典中的“婚姻合同问题”等.直至1944年,冯·诺依曼和摩根斯坦出版著作《博弈论和经济行为》[1],创建了博弈论的一般理论方法,给出了博弈论的一般框架、概念术语和表示方法,这也被公认为博弈论初步形成的标志.一般来讲,可以将博弈分为两大类:合作博弈和非合作博弈.对于非合作博弈,约翰·纳什在1951年提出了“Nash均衡”的概念[2].“纳什均衡”被誉为现代博弈论中最重要的概念,随着博弈论和经济学的发展,纳什均衡已成为现代经济分析的出发点和关键性概念.关于合作博弈,罗伊德·沙普利在1962年提出了“Shapley值”这一重要概念[3],对合作博弈的分配问题做出了重要贡献.
作为一种基本的数学工具,矩阵理论在数学学科与其他学科技术领域,诸如数值分析、优化理论、微分方程、概率统计、运筹学、控制论、系统工程等学科都有广泛的应用,甚至在经济管理、社会科学等领域,矩阵的理论和方法都起着十分重要的作用.同样地,矩阵方法在博弈论的研究中也起着至关重要的作用.实际上,冯·诺依曼就是从矩阵博弈开始研究的[4].近年来,由程代展教授及其团队创立的矩阵半张量积[5-6],打破了传统矩阵乘积对维数的限制,丰富了现代控制领域的研究方法.目前,矩阵半张量积理论已经被成功应用于逻辑系统[7]、有限博弈[8]、图论[9]、有限自动机[10]、生物系统[11]、模糊控制[12-13]等众多领域.基于矩阵半张量积,有限博弈的相关研究取得了一系列丰硕的研究成果.诸如,文献[14]利用半张量积,构建了势方程,给出了势函数的计算方法;文献[15]基于有限博弈的向量空间结构给出了正交分解定理;文献[16]建立了网络演化博弈的代数模型,进而分析了网络的动态行为,包括稳定性、能控性和一致性等问题;文献[17]研究了博弈控制理论在多智能体中的应用;文献[18]研究了基于状态博弈的学习算法设计及其应用,等.
演化博弈最早是由生物学家引入用来研究生物系统的进化过程的[19-21],文献[22]曾指出:“博弈论更容易应用于生物学,而不是它最初设计的经济行为领域”.这充分说明了演化博弈在生物学方面有着很强的应用背景.在过去的几十年里,演化博弈的相关研究吸引了不同学科领域学者们的广泛关注,例如经济系统[23]、社会系统[24]、工程系统[25]等等.对于演化博弈,其动态过程及稳定性是一个自然而不可回避的问题.在矩阵半张量积的研究框架下,文献[26]利用Lyapunov函数对演化博弈的稳定和镇定问题进行了分析,文献[27]讨论了时滞影响下演化博弈的稳定性,文献[28-29]考虑了随机演化博弈的稳定和镇定问题,文献[30-31]分别研究了网络演化博弈和超网络演化博弈的演化稳定策略.
干扰普遍存在于控制系统以及现实生活中,抗干扰问题也得到越来越广泛的关注.值得注意的是,在博弈的相关研究中,大多假设博弈过程在理想的环境中进行.最近,文献[32-33]考虑了干扰影响下的连续时间线性二次博弈,通过ε-Nash均衡来反映干扰对博弈的影响.文献[34]研究了干扰影响下离散非线性二次博弈的事件驱动策略设计.文献[35]考虑了随机干扰对建筑工程供应链中博弈动态过程的影响.并且,文献[32-33]验证了干扰可能会影响博弈动态,最终影响博弈的结果.因此,简单地忽略干扰存在的影响是不合理的.
基于以上讨论,本文利用矩阵半张量积工具,研究干扰影响下演化博弈的稳定与镇定问题.本文的主要贡献如下:1)提出了干扰博弈、控制-干扰博弈、鲁棒-Nash均衡等概念,进而给出了干扰演化博弈与控制-干扰演化博弈的代数状态空间表示.2)通过构造辅助系统,将演化博弈的鲁棒稳定与镇定问题转化为新系统的集合稳定和集合镇定问题.3)给出了干扰演化博弈及控制-干扰演化博弈鲁棒稳定及镇定的充分必要条件,并且设计了状态反馈控制器以保证鲁棒镇定的实现.
本文其余部分的结构安排如下:第2节介绍符号表示、矩阵半张量积的概念和性质.第3节是问题描述,具体给出了演化博弈鲁棒稳定及镇定的概念.第4节是本文的主要内容,分别讨论了干扰演化博弈、控制-干扰演化博弈的代数状态空间表示,给出了鲁棒稳定及镇定的充分必要条件,并进一步设计了状态反馈控制器.第5节通过两个例子验证了本文所得结果的有效性.第6节对本文进行了总结.
2 预备知识
本部分简要介绍一些基本知识,包括符号表示、矩阵半张量积的定义和基本性质.
2.1 符号表示

2.2 矩阵半张量积
本小节简要介绍矩阵半张量积的基本定义和相关性质.
定义1[5]假设A ∈Rm×n,B ∈Rp×q,则矩阵A和B的半张量积定义为
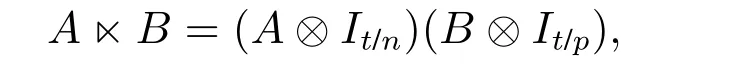
其中t=lcm(n,p)是n和p的最小公倍数.
注意到,当n=p时,矩阵半张量积就退化为传统矩阵乘积.在不致混淆的情形下,符号通常被省略.
引理1[5]下面是关于矩阵半张量积的一些基本性质:

3 问题陈述
本节将具体给出一类干扰影响下演化博弈的稳定与镇定问题的相关介绍和定义.

3)Ξ={1,2,··· ,m}表示外部干扰的集合.
4)C=(c1,c2,··· ,cn)∈Rn,其中ci:S×Ξ →R是第i个玩家的支付函数,i ∈N.
这里“有限”是指:1)玩家个数n<∞;2)策略个数|Si|<∞;3)干扰个数|Ξ|<∞.
下面给出鲁棒Nash均衡的定义.
定义3 给定一个干扰博弈G=(N,S,Ξ,C).

设一个干扰博弈G=(N,S,Ξ,C)被重复进行,那么在每个玩家都是理性的前提,每个玩家都会根据已有的信息更新自己的策略,设法最大化自己的利益.假设n个玩家的局势演化方程可以表示为

其中:wi(t)∈Dai表示系统(2)的内部状态,i=1,2,··· ,p;ξj(t)∈Dlj表示系统(2)的输出,j=1,2,··· ,m.
注1需要指出的是,在工程实践中,各种扰动,例如谐波,恒频波,控制器的增益变化,执行器故障和控制器到执行器通道中的通信波动等都可由外部系统(2)生成[36-37].因此,本文考虑由系统(2)所生成的干扰对博弈的影响.
接下来,给出上述干扰演化博弈GD鲁棒稳定的定义.可以表示为


注2在定义4(定义6)中,要求稳定(镇定)的点是鲁棒-Nash均衡,不失一般性,也可以给出鲁棒稳定(镇定)到任一局势的定义.但众所周知,Nash均衡被认为是非合作博弈的“基本解”,在妥协意义下是每个玩家的最优选择.因此,本文主要考虑演化博弈鲁棒稳定(镇定)到鲁棒Nash均衡的情况,对于一般的收敛性,相关结果可以自然推广.
4 主要内容
在本节中,具体讨论在什么条件下干扰演化博弈(控制-干扰演化博弈)可以实现鲁棒稳定(镇定),并设计状态反馈控制器.
4.1 鲁棒稳定
首先,利用矩阵半张量积,式(1)和式(2)的代数形式可以表示为

并且令z(t)=w(t)x(t)∈Δka.进而,从式(8)和式(9),

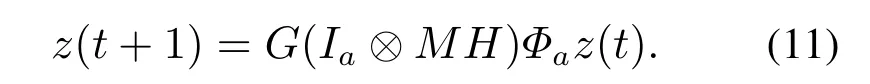
给定一个集合W ⊆Δka.称系统(11)是关于W集合稳定的,如果存在一个正整数η,使得z(t;z0)∈W,∀z0∈Δka,∀t≥η.接下来,将干扰演化博弈的鲁棒稳定问题转化为系统(11)的集合稳定问题.
引理3 干扰演化博弈GD鲁棒稳定到鲁棒Nash均衡s∗,当且仅当系统(11)是关于Λ集合稳定的.
证(必要性) 假设干扰演化博弈GD可以鲁棒稳定到鲁棒Nash均衡s∗,则存在一个正整数ρ,使得式(3)成立.根据式(7),如果w(0)给定,那么{ξ(t)}∞t=0就是已知的.因此,{ξ(t)}∞t=0的任意性就等价于w(0)的任意性.另外,当t≥τ时,w(t)∈Ω,这里τ是系统(9)的过渡周期.因此,令η=max{τ,ρ},则式(3)意味着
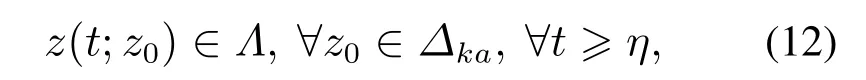
即系统(11)是关于Λ集合稳定的.
(充分性) 假设系统(11)是关于Λ集合稳定的,则式(12)成立.注意到,z(t)=w(t)x(t)是从Δa×Δk到Δka的一一对应.从而,令ρ=η,则式(3)成立,即干扰演化博弈GD可以鲁棒稳定到鲁棒Nash均衡s∗.
证毕.
基于引理3,得到以下定理:
定理1 干扰演化博弈GD鲁棒稳定到鲁棒Nash均衡s∗,当且仅当存在一个正整数η≤ka,使得
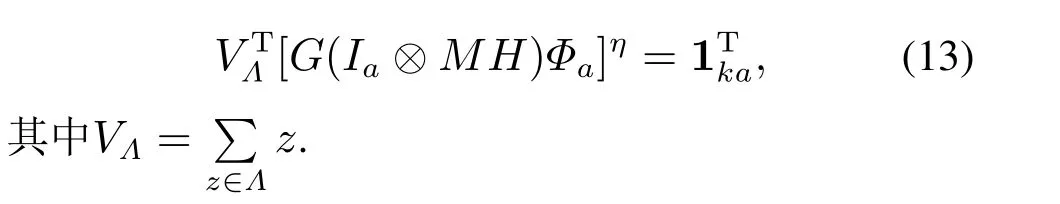
证(必要性) 假设干扰演化博弈GD可以鲁棒稳定到鲁棒Nash均衡s∗,则由引理3,存在正整数η,使得z(t;z0)∈Λ对所有的z0∈Δka和t≥η成立.从而
根据引理3,干扰演化博弈GD可以鲁棒稳定到鲁棒Nash均衡s∗.证毕.
4.2 鲁棒镇定
对于有控制玩家的情形,利用矩阵半张量积将式(4)转化为如下代数形式:
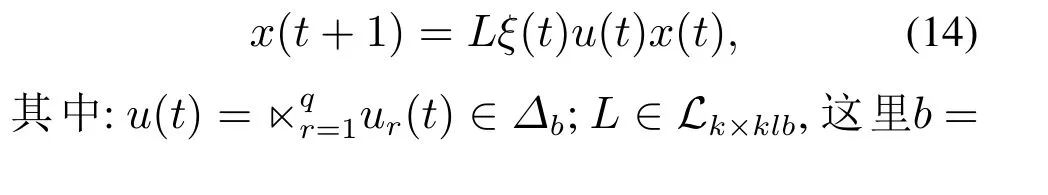

其中“>”指的是两个向量对应分量的元素都满足大于关系.
证
1)⇔2):类似于引理3的证明,易知1)与2)是等价的.


注3根据定理2可以知道,若集合Λ的最大控制不变子集Im(Λ)=∅,那么控制-干扰演化博弈GUD不能被鲁棒镇定到鲁棒Nash均衡s∗.

5 仿真算例
例1 考虑一个干扰博弈G=(N,S,Ξ,C),其中:|N| = 2,|Ξ| = 2,|Si| = 3,i ∈N,且ξ= 1,2时的支付矩阵如表1-2所示.
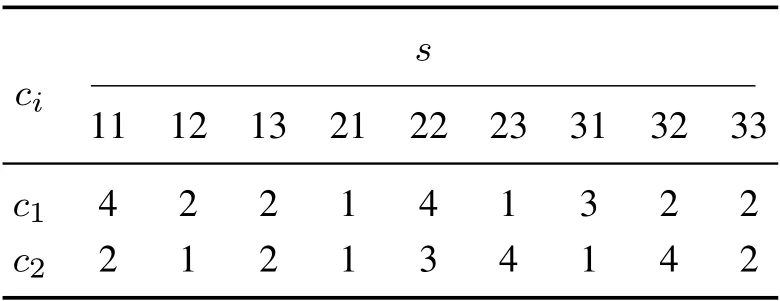
表1 ξ =1时的支付矩阵Table 1 Payoffs when ξ =1
假设重复进行此干扰博弈的动态演化方程为
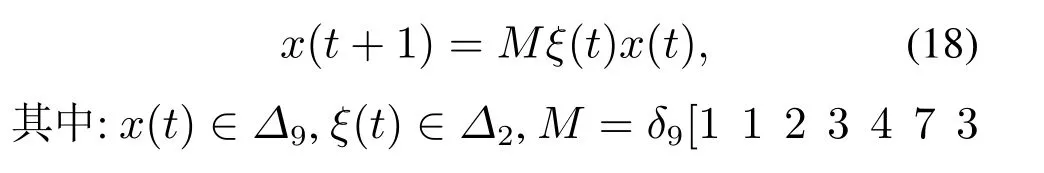

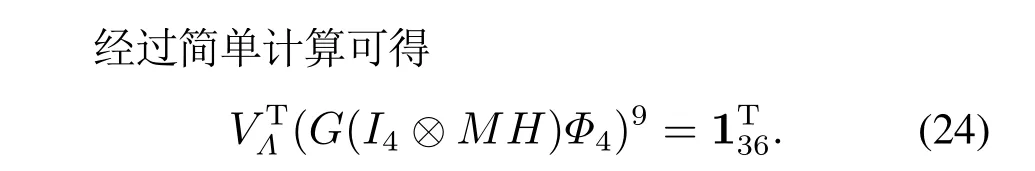
从而,根据定理1可知该干扰演化博弈能够鲁棒稳定到鲁棒Nash均衡s∗.
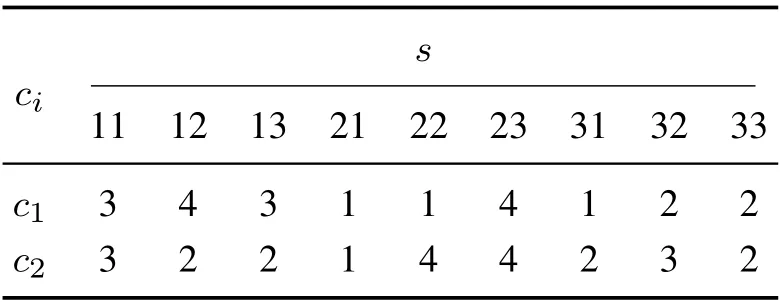
表2 ξ =2时的支付矩阵Table 2 Payoffs when ξ =2
例2 考虑如下控制-干扰博弈G=(N,S,Ξ,C),其中,N=X ∪U,|X|=2,|U|=1,|Ξ|=2,|Si|=3,i ∈X,|Sj|=2,i ∈U,且ξ=1,2时的支付矩阵如表3-4所示.
根据支付信息(表3-4)和定义5,易知s∗=(1,1)~δ19是关于玩家集X的鲁棒Nash均衡.

表3 ξ =1时的支付矩阵Table 3 Payoffs when ξ =1

表4 ξ =2时的支付矩阵Table 4 Payoffs when ξ =2
设外部干扰系统仍为例1中所述,控制-干扰演化博弈的局势演化方程为
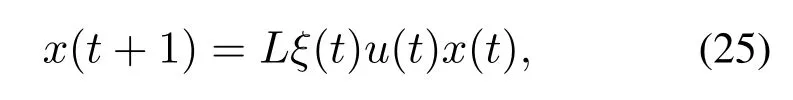
其中:x(t)∈Δ9,ξ(t)∈Δ2,u(t)∈Δ2,且
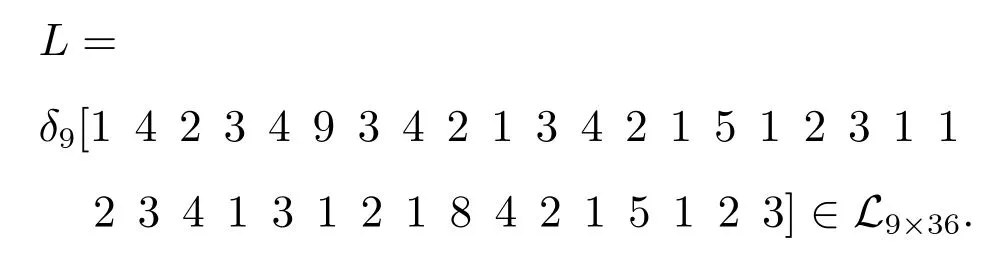
进一步,令z(t)=w(t)x(t)∈Δ36,有如下辅助系统:

换言之,控制玩家可以根据上述所得的状态反馈控制器来更新的自己的策略,以实现该控制-干扰演化博弈鲁棒镇定到s∗.
6 结论
本文研究了演化博弈的鲁棒稳定与镇定问题.在干扰演化博弈与控制-干扰演化博弈鲁棒稳定与镇定等概念的基础上,利用矩阵半张量积得到了代数状态空间表示.进一步,通过构造一个辅助系统,得到了鲁棒稳定与镇定的充分必要条件,并且设计了状态反馈控制器.最后,通过例子验证了所得结论的有效性.

