巧用构造法，妙解导数不等式题

吴仕明

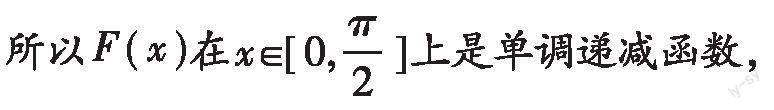
导数不等式问题通常较为复杂，常见的形式有：（1）比较两个函数式或导数式的大小；（2）证明导数不等式；（3）根据恒成立的导数不等式求参数的取值范围.而解答导数不等式问题常用的方法是构造法，即构造合适的函数模型，利用导数中的求导公式、函数的单调性、极值求得问题的答案.

而运用构造法求解导数不等式问题，关键是根据不等式或等式构造出合适的函数模型，通常可根据求导公式、求导法则、函数的特征来构造函数模型.下面举例加以分析.

例1.已知函数的定义域为[R]， [f（-1）=1]，对于任意的[x∈R]， [f（x）>3]，则[f（x）>3x+4]的解集为（     ）.

A. [（-1，1）] B.[（-1，+∞）]

C.[（-∞，-1）] D.[（-∞，+∞）]

解法1.由題意可知[f（x）>3x+4]等价于[f（x）-（3x+4）>0]，

设[g（x）=3x+4]，则[F（x）=f（x）-g（x）=f（x）-3x-4]，

则[F（x）=f（x）-3>3-3=0]，

所以[F（x）]在[R]上单调递增，

又因为[F（-1）=f（-1）-3（-1）-4=0]，

要使[F（x）>0]，需使[x>-1]，所以本题选择B选项.

先将不等式移项，并将不等式左边的式子设为[F（x）]，即可构造出函数[g（x）=3x+4]，[F（x）=f（x）-g（x）=f（x）-3x-4]；然后对函数求导，根据导函数与函数单调性之间的关系判断出函数的单调性，即可根据函数的单调性确定[F（x）>0]时x的取值范围.

解法2.设[f（x）=4x+5]，

由[f（x）>3x+4]可得[x>-1]，所以选择B选项.

由于对于任意的[x∈R]， [f（x）>3]，以及[f（-1）=1]，所以可设[f（x）=4x+5]，将其代入不等式中，即可将导数不等式转化为常规不等式，通过解不等式求得问题的答案.

例2.已知[f（x）]是[（0，+∞）]上的非负可导函数，[xf′（x）+f（x）≤0]，对于任意正数[a，b]，若[a

A. [af（b）≤bf（a）]       B. [bf（a）≤af（b）]

C. [af（a）≤f（b）]        D.[ bf（b）≤f（a）]

解：由[xf（x）+f（x）≤0]可知[f（x）<0]，

则[f（x）]为单调减函数，

即[af（b）≤bf（a）]，所以选择A选项.

对于较为复杂的导数不等式问题，通常可结合题目中的条件和函数的性质，构造出一个合适的简单初等函数，便可根据简单初等函数的性质来快速求得问题的答案.此方法适用于解答填空、选择题.

D. [f（ln2）>0]

解：设[F（x）=f（x）sinx]，

则[F（x）=f（x）sinx+f（x）cosx<0]，

则本题选A.

对于较为复杂的导数不等式问题，同学们要学会从不同的角度寻找解题的突破口，如将不等式化为与求导公式形式一致的式子，将求导前的函数式与简单初等函数相关联，将不等式拆分为几个简单初等函数式，等等，从而构造出合适的函数模型，以顺利破解难题.