启迪学生的数学思考
——“椭圆的标准方程”教学实录及反思*

孙居国 (南京师范大学附属中学 210003)

1 基本情况分析

·教学目标

(1)掌握椭圆的定义及标准方程;(2)理解椭圆的定义过程,掌握椭圆标准方程的推导过程;(3)进一步深化解析几何的基本思想,即几何问题代数化的过程、方法及思想,通过猜想、验证、证明等步骤,学会研究数学问题的一般方法,从而提升数学学科素养．

·教学重点与教学难点

教学重点 椭圆的定义及标准方程.

教学难点 椭圆的定义过程及标准方程的猜想推导过程．

·教学方法与教学手段

教学方法 问题结构驱动教学、启发式教学.

教学手段 多媒体辅助教学．

2 教学过程分析

2.1 问题情境

太阳系中行星的运动轨迹是椭圆．用平行光源照射一个放在地面上的球,适当调整球的位置,球在地面上影子的外轮廓线可以是椭圆(图1)．

图1 图2

启发 图中除了外轮廓线是椭圆,球面上的最高点与最低点在地面上对应的点分别是什么?

由此得出两个特殊的点F1和F2(图2)．

点F1,F2和椭圆上的点有怎样的关系呢?

在画板上取两个定点F1和F2(图3),把一条长度为定值且大于F1F2的细绳的两端固定在F1,F2两点,用笔尖把细绳拉紧,并使笔尖在画板上移动一周,画出的图形是一个椭圆．

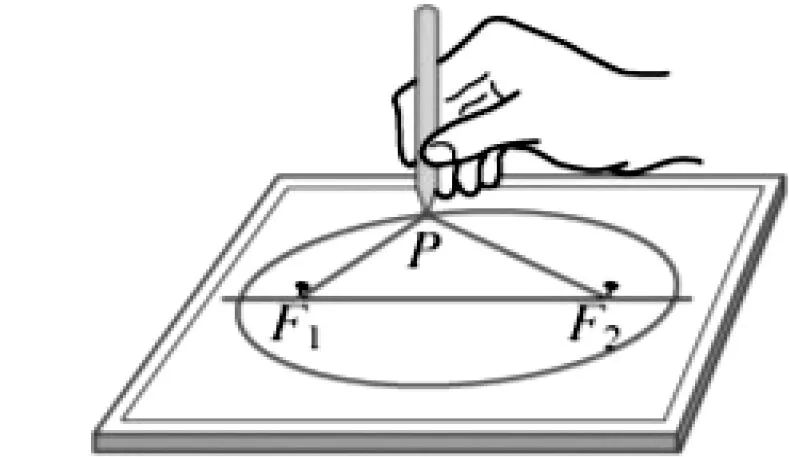
图3

通过师生、生生交流得出椭圆定义:平面内到两定点F1,F2的距离之和等于同一常数(大于F1F2)的点轨迹叫作椭圆,两个定点F1,F2叫作椭圆的焦点,两个焦点间的距离叫作椭圆的焦距．

2.2 学生活动

问题 知道了椭圆的定义后,接下来我们研究什么呢?怎么研究呢?

通过交流协商后,确定研究椭圆的性质、方程等,本课先讨论椭圆的方程．

先看教材[1]上的一段叙述:设椭圆的两个焦点分别为F1,F2,它们之间的距离为2c,椭圆上任意一点到F1,F2的距离之和为2a(2a>2c)．

对这段话的认识很重要,这是圆锥曲线中三种曲线推导的第一种标准方程,应充分体现几何问题代数化的过程,不但要让学生有几何问题代数化的意识,而且要让学生学会如何将几何问题代数化,为以后推导其他曲线的方程提供示范．不妨将问题细化如表1所示．

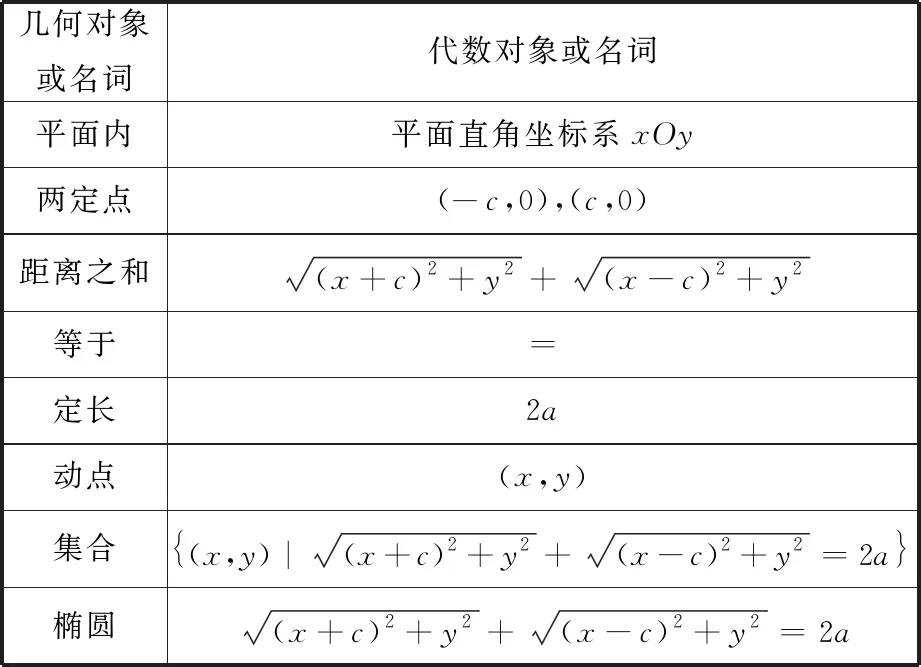
表1 几何对象与对应的代数对象

全面认识课本上的每一句话,充分体现思想性、过程性．

求圆锥曲线方程的第一课是后面学习双曲线方程和抛物线方程的参照和示范,在这一课中,若能让学生发现椭圆在数与形方面表现出的对应过程——即数学家是如何进行试验、联想、类比、猜想的——然后进行分析,并在教学过程中“还原”这一过程,将目标融于过程之中,这对启发学生的数学思维有很大的促进作用．

对于如何化简,课本上往往省略探究过程,很多学生发现直接平方得不出结果或太烦,后来移项平方后才得到结果.这说明我们在进行一个较复杂的运算之前,要对运算的结果进行预估:直接平方会有怎样的结构?若移项平方后,是否简捷一些?教学生在算之前先想一想结论是怎样的、过程是怎样的.

让学生对照椭圆的示意图,猜想椭圆的方程变形后大致是怎样的.圆的方程是一个二元二次方程,椭圆可以看成一个“压扁的圆”,那么椭圆方程是不是也是一个二元二次方程?若是,将是什么样的?

不妨猜想椭圆的方程为Ax2+Bxy+Cy2+Dx+Ey+F=0 ①,由于椭圆关于y轴对称,故有Ax2-Bxy+Cy2-Dx+Ey+F=0 ②．

①②两式对于任意x都成立,即Ax2+Bxy+Cy2+Dx+Ey+F=Ax2-Bxy+Cy2-Dx+Ey+F,所以B,D均为0．同理可得E也为0．因此,椭圆方程的形式应为Ax2+Cy2+F=0．

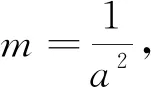
通过这样的猜想推断,学生对椭圆方程己有初步的认识．

2.3 建构数学

学生尝试推导,学生板演,三种思路.一是直接平方,有点麻烦,没得出结果,过程很烦,建议课后继续化简.二是移项后平方,与课本中方法相同,学生板演顺利.三是下列方法:

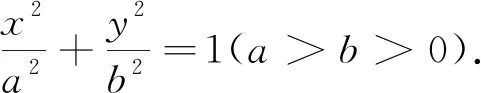
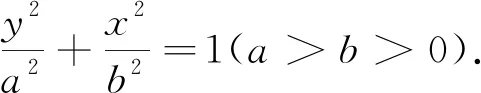
这样做的特点是对学生的思维要求高:注意思维的过程与细节,时刻注意数与形的渗透和转换,体现了为什么要化成标准方程,展示了一个结论生成过程的诸多问题,体现了椭圆方程的本质特征．因此,教学中应尽可能把知识的发生过程转化为一系列带有探索性的问题,为学生提供猜想的空间,经历学习、探究的过程．真正使有关材料成为学生的思考对象,使数学学习成为学生的内在需求,从而启发学生的数学思维．

2.4 反思延伸

课本中在推导完椭圆标准方程后,得出这样的结论:“由上述过程可知,椭圆上的点的坐标(x,y)都满足方程,并且满足此方程的点(x,y)都在椭圆上．”为什么满足此方程的点(x,y)都在椭圆上?这一细节交待得并不清楚．

“满足此方程的点(x,y)都在椭圆上”这句话看似显然,实则很深奥．要说明下面三点:一是什么叫“点(x,y)都在椭圆上”?学生对它的意义还不清楚.二是为什么“点(x,y)都在椭圆上”?学生对它的过程不清楚.三是为什么要说明“点(x,y)都在椭圆上”,学生对它的本质不清楚．

如果学生明白了上述三个为什么,那么对解析几何的本质“几何问题代数化”就有了更加深刻的认识．“点(x,y)都在椭圆上”的意义是“满足方程的解为坐标的点在椭圆上”,其过程需要严谨的证明,这是曲线与方程定义所决定的．

因此,对这一细节处理如下:

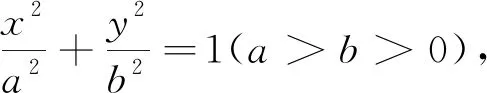
通过这一过程,不但完善了课本中的结论,而且将结论融于这些细节之中,从而启发学生的数学思考,使学生逐渐学会用数学的眼光去看问题、用数学的思维去思考问题,启发了学生的思维,也为后续曲线与方程的定义打下了基础．

2.5 本课小结

知识层面:(1)椭圆定义;(2)椭圆标准方程．

思想方法和素养层面:(1)几何问题代数化的思想方法;(2)猜想、验证、证明等研究问题的一般方法步骤．

正如数学家陈省身所言:“数学是自己思考的产物,首先要能够思考起来,用自已的见解和别人的见解交换,才会有很好的效果．”数学思考是数学学习中最有价值的行为．

2.6 课后作业

作业:普通高中数学教科书·选择性必修第一册(苏教版2021)第79页练习1～5．

3 教学反思

数学思考是数学教学所有行为中最有价值的行为,在教学中若离开了数学思考,只有题型模仿、类型强化、技能操练,也只能是教学中的无效或低效行为．有思考才会有问题,才会有探究,才会有反思,才能深入理解数学内容的本质.因此,课堂上要让学生能够思考起来,用自已的见解和别人的见解交换,才会有很好的效果．

《普通高中数学课程标准(2017年版)解读》中指出:数学学科核心素养本质上反映的是数学的思维品质,基于核心素养的数学课堂应立足于学生思维品质的培养而成为“思维之树常青”的课堂,因而,“启发学生的数学思考”就成为高中数学教学的关键[2]．这要求一线教师立足于高中数学课堂主阵地,做课堂教学中的有心人,在每一个时刻关注学生的认知,在每一个细节留心学生的想法,把启发学生的数学思考落到实处,让学生的思维之花盛开于数学课堂上,从而发展学生的数学素养,落实立德树人的根本任务．