关于光滑流形Spark特征的注记

陈洪宇, 黄开河, 薛 涵, 杜承勇

(四川师范大学 数学科学学院, 四川 成都 610066)

1 预备知识

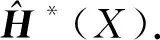
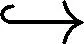
因此,为了进一步研究清楚这些spark复形的spark特征的同构关系,需要找到更一般的spark复形同态使得它们可以诱导spark特征的同构.在本文中,首先找到一类满足这一条件的spark复形同态,称之为拟同构(定义2.2).

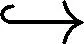
本文第3.3节,将构造一个新的上链spark复形SΓ,使得SCS⊆SΓ⊆SCH是子复形含入,而且构造出spark复形同态

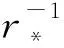
定理 1.2(同定理4.6) 有一个具体的spark特征同构

本文结构如下:首先,在第2节中整理spark复形的基本概念与性质,并证明拟同构诱导spark特征的同构,即定理1.1;然后,在第3节中回忆SU与SCS和SCH的构造,并构造出SΓ;最后,在第4节中研究这些spark复形的关系,并证明定理1.2.

2 Spark复形

一个同调spark复形[1,5-6],或简称为spark复形,是一个上链复形的三元组S:=(F*,E*,I*),满足:

1)I*与E*都是F*的子复形;

2) 当k>0时Ik∩Ek={0},当k<0时Fk=Ek=Ik={0};

3)H*(E*)≅H*(F*).

一个元素a∈Fk若满足spark方程

da=e-r,e∈Ek+1,r∈Ik+1,

(1)

则称之为一个度为k的spark.2个度为k的sparks a和a′称为等价,如果它们满足

a-a′=db+s,b∈Fk-1,s∈Ik.

(2)

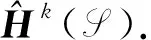
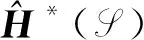
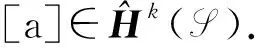
一个spark复形同态

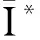
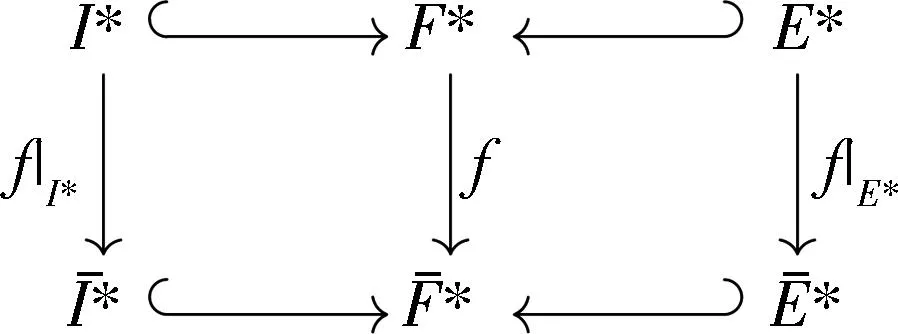
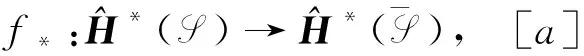
定理 2.3如果

是spark复形拟同构,则它诱导spark特征的同构

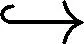
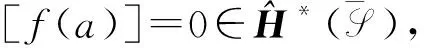
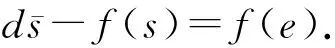
由引理2.1,ds=0,[s]∈H*(I*).所以

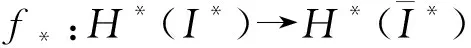
而

d(a-s′-t)=e+r-ds′-dt=r-dt=0,所以[a-s′-t]∈H*(F*),而且

f*([a-s′-t])=[f(a-s′-t)]=

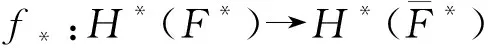
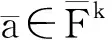
(3)

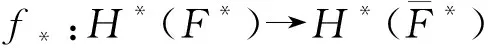
也即是

(4)

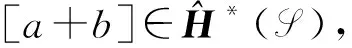
因此f也是满射.

3 光滑流形的spark复形

本节先回忆文献[1]中光滑流形的光滑hyperspark复形、Cheeger-Simons spark复形和上链hyperspark复形的构造,并引进一个新的spark复形:上链spark复形.

3.1 光滑hyperspark复形首先回顾光滑hyperspark复形的构造.设U={Ui|i∈I}是光滑流形X中局部有限开覆盖.有双复形

它的2个微分算子为

D=D′+D″.

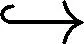
r将一个q-形式ω∈Ωq(X)嵌入到C0(U,Ωq)中.下面的结果是经典的,参见文献[7].

引理 3.1(广义Mayer-Vietoris原理) 对每个q≥0,复形

(5)

是正合的.

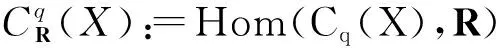
(6)

由de Rham定理可知此上链复形嵌入是拟同构.显然

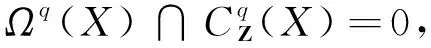
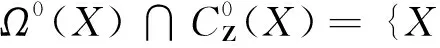
所以有spark复形

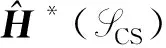
定理 3.2[1]我们有

文献[1]构造了上链hyperspark复形SCH并证明了存在子spark复形的含入同态因此

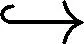
为了实现这一点,本文将会构造一个新的spark复形SΓ,称为上链spark复形,并构造出spark复形同态:

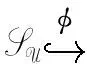
(7)

接下来首先回顾上链hyperspark复形SCH的构造,再给出上链spark复形SΓ的定义.

3.3 上链hyperspark复形与上链spark复形上链hyperspark复形与上链spark复形都是用光滑奇异上链的芽层构造的.因此先回顾一下光滑奇异上链的芽层.

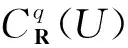
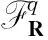
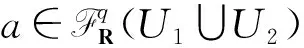
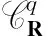
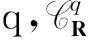
1) Supp(li)⊆Ui;

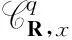
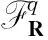
(8)

(9)

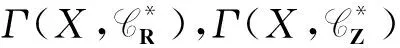
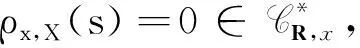
因为

(10)

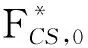
设Aq是q次微分形式的芽层(因此也是微分形式的预层),则

Aq(U)=Γ(U,Aq)=Ωq(U).

将(6)式应用于每个开集U⊆X,可得群的单态射

(11)

特别地,这个态射是单射.

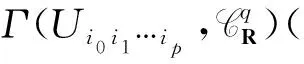
光滑奇异链的边缘算子∂诱导了层的链复形

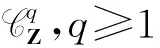
定义 3.5光滑流形X的相应于局部有限开覆盖U的上链hyperspark复形为

当开覆盖只有一个开集{X}时,得到

定义 3.6光滑流形的上链spark复形为

4 光滑流形的4个spark复形的关系

本节将完整地研究3.3中的所有4个spark复形之间的同态,即

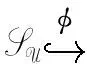
4.1spark复形SU和SCH之间的拟同构通过(11)式中的φ得到了一个spark复形单同态

φ:SU→SCH.

引理 4.1当U是good开覆盖时,φ:SU→SCH是拟同构.

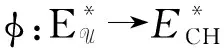
另一方面,注意到

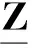
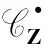
(12)

则

于是有

因此当U是good开覆盖时,有

(13)

证毕.

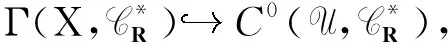
证明这是因为

接下来构造一个反向的拟同构

f:SCH→SΓ.

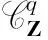
它的具体构造如下.首先从li出发可以定义一个同伦算子

其中

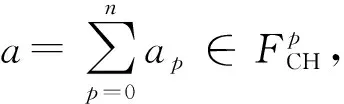
类似于文献[7]第9节的计算可得:

引理 4.3f是一个链复形同态

此外

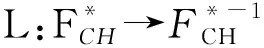
DL+LD=id-ι∘f,它是由

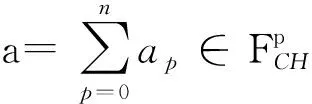
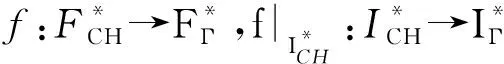
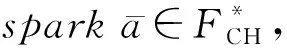
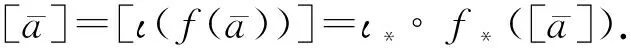
4.3spark复形SCS和SΓ之间的拟同构由正合列(8)和(9)式可以得到一个spark复形同态

r:SCS→SΓ.

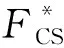
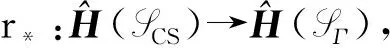
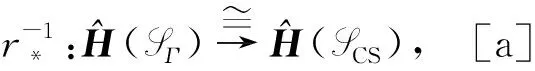
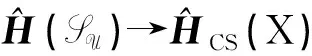
定理 4.6有spark特征同构

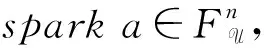
由Da=e+s可知

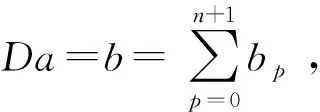
D(φ(a))=φ(b)=φ(e)+φ(s)=e+φ(s).

所以

∂(f∘φ(a))=f(D(φ(a)))=

f∘φ(e)+f∘φ(s)=e+f∘φ(s),由推论4.5可得

r(a′)=f∘φ(a),da′=f∘φ(e)+s′=e+s′,r(s′)=f∘φ(s).