加权概率犹豫模糊集多属性群决策算法及应用
朱国成
(广东创新科技职业学院 人文教育学院, 广东 东莞 523960)
0 引言
在概率犹豫模糊集多属性群决策(probabilistic hesitant fuzzy sets multiple-attribute group decision making,PHFSMAGDM)问题中,主要从决策专家的权重确认方法[1-2]、属性权重的计算方法[3-4]、决策算法[5-6]等3方面进行研究.由于给予决策专家赋权时,主观赋权受外界的影响因素广泛,故随意性较大.同时,客观赋权法仅从数据出发,虽然具有很强的数学理论依据,但是在实际决策问题中决策者非常容易从情感层面淡化对于属性的重要性感知.鉴于此,为了克服决策专家主客观单独赋权方法的不足,组合赋权法[7]被采用(将主观赋权法与客观赋权法进行结合).本文为了确认决策专家的权重,基于离差最大化思想计算决策专家的客观权重,再根据客观权重与主观权重的相离程度最终确定决策专家的综合权重.在计算属性权重方法方面,一般做法有熵值法[8]和离差最大化方法[9]等,二者都是从各个方案在属性上的决策数据信息差异角度考虑,进而计算出属性的权重(在此种情形计算出的属性权重本文称为整体权重).目前鲜有文献从单个方案在所有属性上的内部决策数据信息差异考虑,进而算出该方案在所有属性上的内部得分值差异大小,然后再计算出所有方案在所有属性上的内部得分差异值,最终根据各方案在各属性下的内部得分差异程度计算出属性的权重(在此种情形计算出的属性权重本文称为个体权重),最后,再利用属性的整体权重与个体权重来计算属性的综合权重.在决策算法方面,王志平等[10]建立了一种将逼近理想解的排序法(technique for order preference by similarity to an ideal solution,TOPSIS)与前景理论相结合的决策模型;付超等[11]在TOPSIS框架下解决了概率犹豫直觉模糊集多属性群决策问题.
有别于前人针对PHFSMAGDM问题的研究,本文首先引入了一个新的概念——加权概率犹豫模糊集(weighted probabilistic hesitant fuzzy sets,WPHFS).WPHFS中的元素称为加权概率犹豫模糊元(weighted probabilistic hesitant fuzzy elements,WPHFE),其主要特点是,每个可能作为隶属度值的数值都被赋予了决策专家的综合权重,用来对隶属度值的重要性进行注解.其次,将加权概率犹豫模糊数(weighted probabilistic hesitant fuzzy numbers,WPHFN)用三维点坐标进行刻画,在此基础上提出了WPHFE的相关运算(计算WPHFE的三维得分值、三维离差值和2个加权概率犹豫模糊元的几何距离等),利用WPHFE的相关运算给出了计算属性的综合权重方法.再次,根据离差最大化思想来计算决策专家的综合权重.结合决策专家的综合权重与属性的综合权重提出了一种确定正理想方案与负理想方案的方法,并基于TOPSIS思想建立一种新的贴近度公式,利用新的贴近度公式来达到排序方案目的.最后,通过一个具体算例来验证文中方法的可行性.
1 预备知识
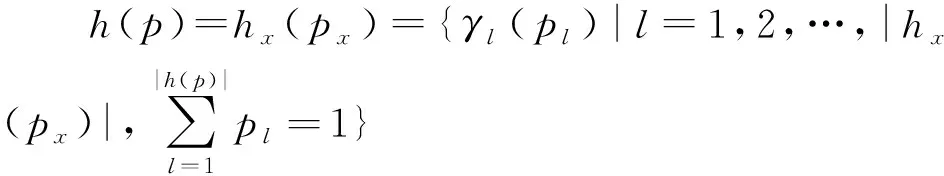

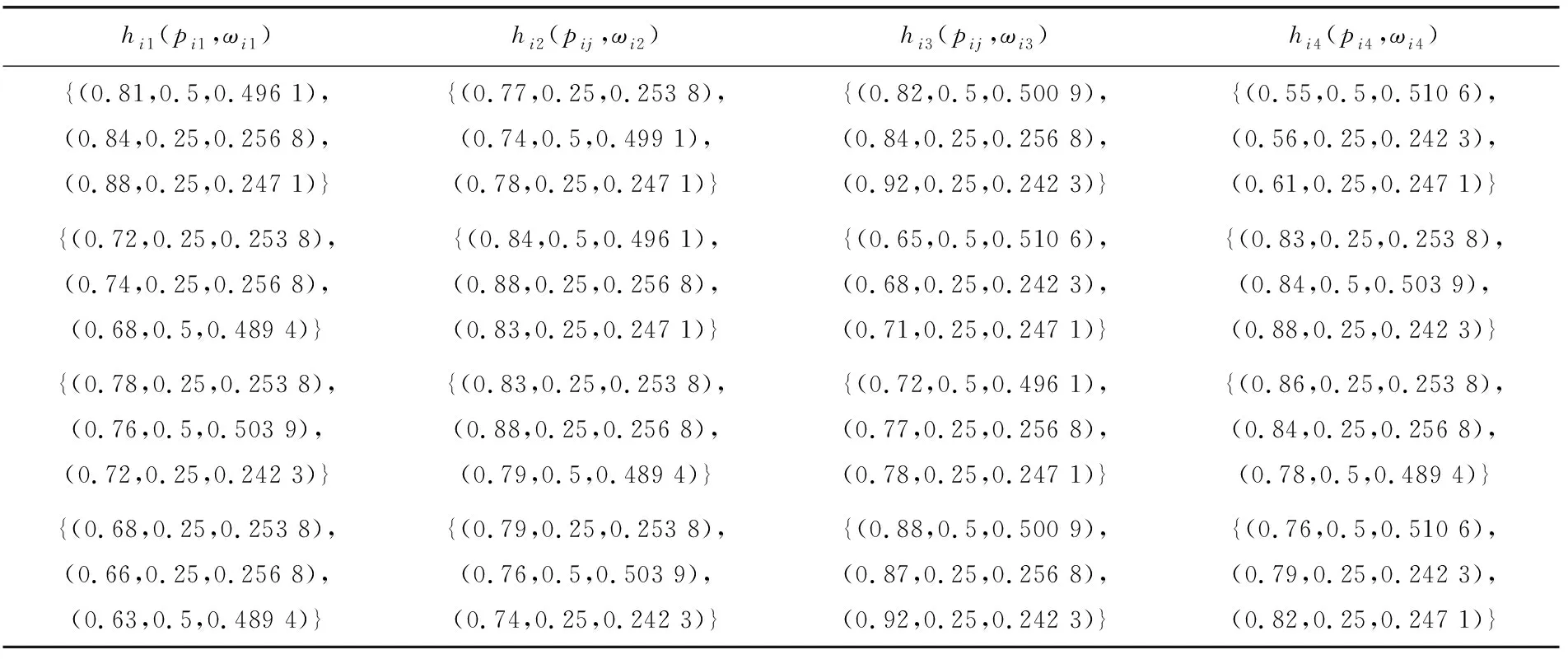
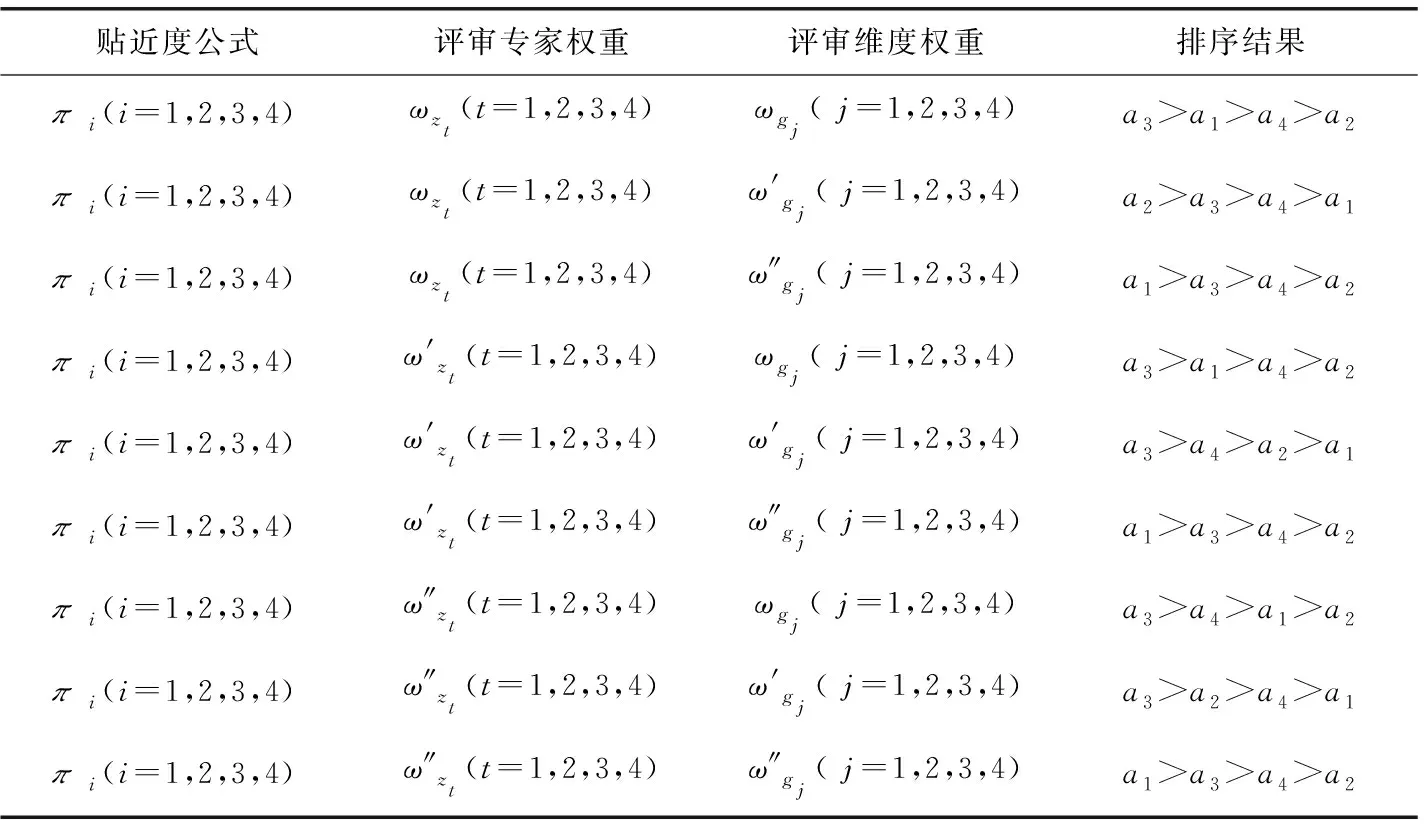
1) 若s(h1(px)) 2) 若s(h1(px))>s(h2(px)),则h1(px)≻h2(px); 3) 若s(h1(px))=s(h2(px)) ,则有: ①d(h1(px))>d(h2(px))⟹h1(px)h2(px),②d(h1(px)) 定义 3[13]设任意2个PHFEh1(p)与h2(p),二者之间的海明距离dH(h1(p),h2(p))定义为 dH(h1(p),h2(p))= 陈述 1 由定义1可知,PHFS与犹豫模糊集(hesitant fuzzy sets,HFS)相比,在描述决策信息时更具有优势,因为决策者在刻画属性信息数据时不但具有更加宽泛的信息表达能力,而且还能够体现决策群体的决策意向.故,PHFS能够更加细腻地描述决策者的决策行为.然而在利用PHFS来解决多属性群决策问题时还具有一定的局限性(在获取各方案的综合属性值时,虽然决策专家的重要性信息可以由集成算子体现,但是在原始的PHFS中决策专家的重要性信息却被忽略了).例如,对于有3位决策专家(甲乙丙)构成的决策问题,甲的权重为0.6,乙、丙的权重皆为0.2,对某事物进行评价时,甲给出了0.6的评价数据,乙、丙2位专家皆给出了0.8的评价数据,此时PHFS可以描述为{0.6(1/3),0.8(2/3)}.由此可知,虽然PHFS中的隶属度值0.6与0.8蕴含了概率信息,但是其分别具有的重要性却没有显示出来.若对于隶属度值0.6与0.8分别关联决策专家的重要性数据信息,PHFS可以进一步描述为{0.6(1/3,0.6),0.8(2/3,0.4)}. 陈述 2 由定义2可知,在判断2个PHFEh1(px)与h2(px)的大小时,利用的是得分函数与方差,在计算得分函数时只是将隶属度与之概率这2个维度的数据信息简单相乘,这样做虽然能够比较2个PHFEh1(px)与h2(px)的大小,但是也容易造成决策信息失真.同时,在对PHFE中的数据信息进行集结时,随着其元素——概率犹豫模糊数(probabilistic hesitant fuzzy numbers,PHFN)数量的增加,概率信息数据的集结结果会高速趋向于0.为了解决此类问题,一般做法是对概率犹豫模糊信息的运算进行归一化处理,但是,当PHFS中添加了能够反映决策专家重要性程度的信息以后,定义2则不再适用. 陈述 3 由定义3可知,在计算2个PHFEh1(px)与h2(px)海明距离时,2个PHFE中的内部元素个数需要一致,若不一致则需按照某种规则对PHFEh1(px)与h2(px)添加或减少适量的元素.同时,在具体的运算过程中,只是2个PHFEh1(px)与h2(px)中相对应位置的元素进行测度,完全忽略了2个PHFEh1(px)与h2(px)中其他元素之间的关系. 根据陈述1、陈述2和陈述3,本文对PHFS进行了再定义(给予PHFS中的隶属度添加了相应的决策专家综合权重来定义了WPHFS,并以点坐标形式描述WPHFS),给出了判断2个WPHFEh1(px)与h2(px)的大小规则以及建立了测度2个PHFEh1(px)与h1(px)的距离模型(几何距离),有定义4、定义5、定义6如下. 定义 5WPHFEhx(px,ωx),称 (1) 为WPHFEhx(px,ωx)的三维得分值,称 d(hx(px,ωx))= 为WPHFEhx(px,ωx)的三维离差值. 在三维得分值与三维离差值的基础上,判断2个WPHFEh1(px,ωx)与h2(px,ωx)的大小准则定义为: 1) 若s(h1(px,ωx)) 2) 若s(h1(px,ωx))>s(h2(px,ωx)),则h1(px,ωx)≻h2(px,ωx); 3) 若s(h1(px,ωx))=s(h2(px,ωx)) ,则有: ①d(h1(px,ωx))>d(h2(px,ωx))⟹h1(px,ωx)h2(px,ωx),②d(h1(px,ωx)) 定义 5中WPHFEhx(px,ωx)的三维得分值类似于定义2中PHFEhx(px)的得分函数,但是,定义5中WPHFEhx(px,ωx)的三维得分值可以有效减缓随着WPHFEhx(px,ωx)中元素数量的增加导致的概率信息数据及决策专家权重数据在集结时快速趋向于0的问题.定义5中的WPHFEhx(px,ωx)的三维离差值类似于定义2中PHFEhx(px)的方差,二者都能直观反应PHFE中内部元素的相离程度,因为在计算三维得分值与三维离差值时,皆是WPHFEhx(px,ωx)内部相同维度的数据信息进行测度,只是在计算最终结果时才将不同维度的信息数据进行糅合,所以该做法可以尽量避免在计算WPHFEhx(px,ωx)值的过程中的信息丢失.综上,可以依据定义5对2个WPHFEh1(px,ωx)与h2(px,ωx)进行大小比较. 以1个例子来说明定义5的有效性及添加决策专家综合权重的必要性. 例 1比较PHFEh1(p)={0.6(0.5),0.4(0.5)},h2(p)={0.6(0.6),0.5(0.4)}的大小. 解若按照文献[14]针对2个PHFE的大小判断准则,可得PHFEh1(p)、h2(p)的得分函数值为s(h1(p))=0.5,s(h2(p))=0.56,即有h1(p)h2(p). 若在PHFEh1(p)、h2(p)中给予隶属度添加决策专家平均权重,此时可将WPHFEh1(p)、h2(p)描述为h1(p)={(0.6,0.5,0.5),(0.4,0.5,0.5)},h2(p)={(0.6,0.6,0.5),(0.5,0.4,0.5)}.按照定义5的比较方法,可得s(h1(p))=0.435 0,s(h2(p))=0.449 3,即有h1(p)h2(p). 若在PHFEh1(p)、h2(p)中给予隶属度添加决策专家的综合权重,不妨将2个WPHFE描述为h1(p)={(0.6,0.5,0.9),(0.4,0.5,0.1)},h2(p)={(0.6,0.6,0.4),(0.5,0.4,0.6)}.按照定义5的比较方法,可得s(h1(p))=0.459 9,s(h2(p))=0.453 9,即有h1(p)≻h2(p). 由上述例1可知,若将决策专家的平均权重注入PHFE中,则不会改变2个WPHFE的大小,因而说明了定义5的有效性(与文献[14]得出的排序结果相同).若将决策专家不同的权重加入PHFE中,则得到了2个WPHFE相反的排序结果,这说明在2个PHFE的大小比较中,决策专家的权重所起到的作用不容忽视.进一步说明了将决策专家权重注入PHFS中的必要性,考虑到决策专家的综合权重相较于其主观权重或客观权重能够更全面地反映决策作用.故可知,本文在PHFS中添加决策专家的综合权重更加科学. 定义 62个WPHFEh1(px,ωx)与h2(px′,ωx′),其中 h1(px,ωx)={(γl,pl,ωl)|l=1,2,…, h2(px′,ωx′)={(γl′,pl′,ωl′)|l′= 1,2,…,|h2(px′,ωx′)|, 则WPHFEh1(px,ωx)与h2(px′,ωx′)之间的几何距离定义为 δd(h1(px,ωx),h2(px′,ωx′))= (3) 容易证明δd(h1(px,ωx),h2(px′,ωx′))∈[0,1],δd(h1(px,ωx),h2(px′,ωx′))与定义3中的2个PHFEh1(p)与h2(p)的海明距离相比,(3)式的几何距离充分考虑了WPHFEh1(px,ωx)与h2(px′,ωx′)内部之间的所有元素之间的关系,故δd(h1(px,ωx),h2(px′,ωx′))计算的结果所包含的信息更加全面也更具普遍性.同时,在具体计算时,WPHFEh1(px,ωx)与h2(px′,ωx′)之间的内部元素数量也无需相等. 2.1 计算决策专家综合权重(ωzt) 第1步 计算每位决策专家关于某个方案在某个属性上的权重 t=1,2,…,T. (4) 第2步 计算每位决策专家针对所有方案在某个属性上的权重 (5) 第3步 计算每位决策专家关于所有方案在所有属性上的客观权重 (6) 2) 计算ωzt.本文根据决策专家客观权重与主观权重相离程度来最终确定其综合权重,二者相离程度越大说明决策过程中该专家发挥作用越不稳定,则将该决策专家的权重相应越小. t=1,2,…,T. (7) 2.2 计算属性综合权重本文属性的综合权重由属性的整体权重与个体权重两部分计算得出.首先,根据所有方案在所有属性上的得分差异值来计算属性的权重(此种计算属性权重的方法叫熵值法),得出的属性权重称为整体权重.另外一种计算属性权重的方法得出的属性权重称为个体权重,计算方法为:①确定单个方案在所有属性上的得分值(由WPHFE信息数据构成),并计算WPHFE的三维离差值,进而算出该方案在所有属性上的三维离差值占比;②计算所有方案在所有属性上的三维离差值占比;③根据所有方案在所有属性上的三维离差值占比之间的差异程度值确定属性的权重;④取属性的整体权重与个体权重之和的一半作为属性的综合权重.具体计算过程如下. 第1步 计算决策专家的综合权重ωzt. 第2步 根据定义7,将决策专家给予方案的初始信息表转换为由WPHFEhij(pij,ωij)构成的数据信息表. 第3步 利用定义5计算WPHFEhij(pij,ωij)的三维得分值s(hij(pij,ωij)=sij. 第1步 计算决策专家的综合权重ωzt. 第2步 根据定义7,将决策专家给予方案的初始信息表转换为由WPHFEhij(pij,ωij)构成的数据信息表. 第3步 利用定义5,计算WPHFEhij(pij,ωij)的三维离差值d(hij(pij,ωij))=dij. 第5步 求属性gj下的熵值 3) 确定属性的综合权重 (8) 由(8)式及计算属性的整体权重与个体权重过程可知,属性的综合权重ωgj不但考虑了方案间的整体得分值差异,而且还兼顾了在所有属性上同一个方案内部之间的得分值差异,故本文计算出的属性综合权重在实际应用中具有更大应用价值. 2.3 决策步骤 第1步 计算决策专家的综合权重ωzt. 第2步 依据定义7,将决策专家给予方案的初始评价信息表转换为由PHFEhij(pij,ωij)构成的数据信息表. 第3步 确定属性的综合权重ωgj. 第4步 根据WPHFEhij(pij,ωij)构成的决策数据信息表选取正理想方案(a+)与负理想方案(a-),分别有: 其中 (9) (10) 第6步 基于TOPSIS思想建立贴近度 (11) 一般情况下,贴近度πi越大其对应的方案ai越优. 第7步 结束. 表 1 论文评审数据信息 表 2 PHFEhij(pij,ωij)(i, j∈{1,2,3,4})决策数据信息 d11=0.748 3,d12=0.720 7,d13=0.804 6,d14=0.785 2,d21=0.712 7,d22=0.752 3,d23=0.766 4,d24=0.769 2,d31=0.779 4,d32=0.757 2,d33=0.721 5,d34=0.719 6,d41=0.710 1,d42=0.768 6,d43=0.763 5,d44=0.766 4. 3) 由1)和2)可得评审维度的综合权重ωgj(j∈{1,2,3,4})分别为 ωg1=0.400 3,ωg2=0.171 0,ωg3=0.222 8,ωg4=0.206 1,这里 0.000 2是在计算过程中采取四舍五入的方法造成的误差值. 3.3 决策过程 第1步 由3.1与3.2节已知评审专家的综合权重与评审维度的综合权重分别为 ωz1=0.253 8,ωz2=0.256 8,ωz3=0.242 3,ωz4=0.247 1,ωg1=0.400 3,ωg2=0.171 0,ωg3=0.222 8,ωg4=0.206 1. 第2步 依据定义7,将评审专家给予文章的初始信息表转换为由WPHFEhij(pij,ωij)构成的数据信息表,见表2. 第3步 确定正理想文章(a+)与负理想文章(a-),得 a+={(0.88,0.5,0.503 9),(0.88,0.5,0.503 9),(0.92,0.5,0.510 6),(0.88,0.5,0.510 6)},a-={(0.63,0.25,0.242 3),(0.74,0.25,0.242 3),(0.65,0.25,0.242 3),(0.55,0.25,0.242 3)}. 可得 π1=0.434 2,π2=0.403 9,π3=0.443 1,π4=0.418 9,由本文排序规则可知,4位评审专家给出的4篇文章排序依次为a3>a1>a4>a2. 3.4 决策模型比较按照文中排序模型,评审专家与评审维度分别取不同形式的权重,依次可得各篇文章的排序结果,见表3. 表 3 9种决策模型的排序结果 WPHFS作为PHFS的拓展,可以在原始集合中保留决策专家的重要性信息,采用三维点坐标表示的WPHFS可以有效解决陈述1~3中的问题,因而WPHFS非常便于处理复杂的PHFS多属性群决策问题.论文的主要工作有,制定了判断2个WPHFE的大小比较规则,建立了测度2个WPHFE的距离模型,探讨了计算决策专家综合权重与属性综合权重的计算方法,并在决策案例中对本文决策模型进行了验证分析,由数值算例对比结果可以得到以下结论: 1) 从维度的角度出发定义的WPHFS决策算法可以达到排序方案的目的. 2) 在决策过程中,考虑决策专家主客观权重进而计算其综合权重是必要的. 3) 利用熵值法计算属性权重时,仅考虑从各方案在属性上的整体得分差异程度计算属性权重的因素不够全面,因为各个方案在属性上得分的内部差异程度对属性权重的再分配进而对决策结果的影响至关重要. 4) 在整个决策过程中,属性综合权重对于方案排序结果的影响程度大于决策专家综合权重对于排序结果的影响程度. 文中方法也存在不足之处,需要进一步完善,例如对新定义的WPHFS的科学性没有进行理论推导与证明,虽然新定义的WPHFS能够解决PHFS多属性群决策问题,但是其能否在实践中进行推广有待验证;新建立的判断2个WPHFE的大小比较规则与测度2个WPHFE的距离模型都能分别达到应用目的,但是其科学性没有理论证明,同时关于其分别具备的性质也没有深入挖掘;文中决策模型缺少与其他文献中的模型进行有效对比等.对于以上不足之处,今后作者将进一步研究. 致谢广东创新科技职业学院特色创新类重点资助项目(2023TSZD05)对本文给予了资助,谨致谢意.
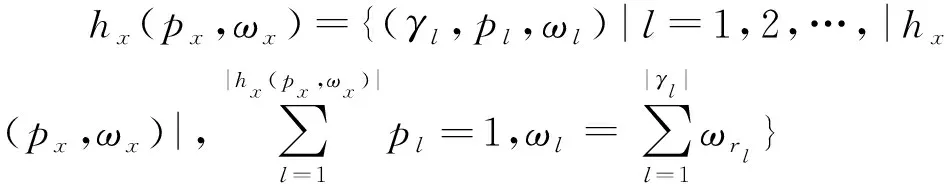
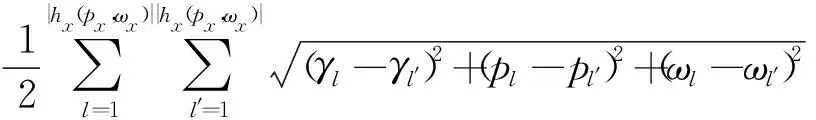
2 主要方法与结果
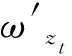
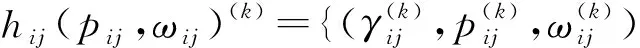
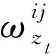
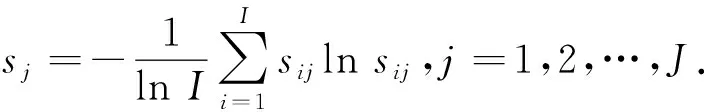
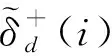
3 算例分析
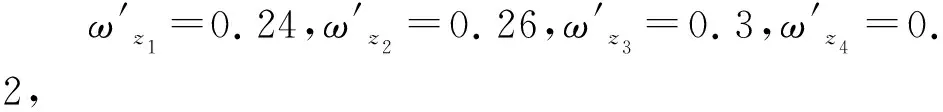
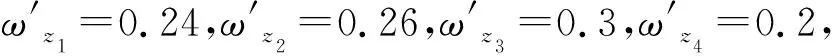

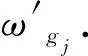

4 结论

