几类一元模糊代数方程的可解性条件
苏 欢, 潘小东, 付 凯
(西南交通大学 数学学院, 四川 成都 611756)
自1965年Zadeh引入模糊集合[1]的概念以来,由于其极其广泛的应用需求,模糊集理论及其应用受到了众多学者的广泛关注[2-5].经过近60年来的发展,模糊集合无论是在理论还是在应用方面都取得了长足的进步[6-8].Zadeh的模糊集合是对模糊概念外延的形式化描述,但其定义过于宽泛,并没有反映出模糊现象的本质及其主要特征,正是由于这个原因,难以确定其隶属函数也成为模糊集理论和应用研究过程中出现诸多争议的关键所在.尽管许多学者对Zadeh的模糊集概念从不同角度进行了扩展[9-12],也取得了许多很有意义的研究成果[13-17],但并没有从根本上解决这个问题.
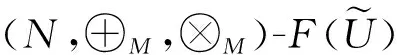
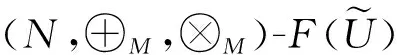
1 预备知识
下面主要介绍序与格以及公理化模糊集合理论的一些基本概念、结论和记号.
定义 1.1[21]非空集合E上的二元关系R若具有自反性、反对称性和传递性,则称R为E上的序关系或偏序关系.
定义 1.2[21]设(E,≤)为偏序集,D⊆E.如果D具有以下性质
∀x∈D,y∈E,y≤x⟹y∈D,则称D为E的下集.对偶地,定义上集为满足以下条件的子集
∀x∈D,y∈E,y≥x⟹y∈D.
定义 1.3[22]在一个偏序集(L,≤)中,如果任意2个元素x、y都有上确界x∨y和下确界x∧y,则称偏序集(L,≤)为一个格.
定义 1.4[22]设S是格L的一个子集,若∀a,b∈S,总有a∧b∈S,a∨b∈S,则称S为L的一个子格.如果还满足:∀a,b∈S,∀x∈L,如果a≤x≤b,则x∈S,这时称S为L的一个凸子格.
定义 1.5[22]设L是一个格,如果L的任意非空子集S都有上确界∨S和下确界∧S,则称L是完备格.
定义 1.6[21]设L是一个格,如果对L中的任意元x、y、z都有:
1)x∧(y∨z)=(x∧y)∨(x∧z),2)x∨(y∧z)=(x∨y)∧(x∨z),则称L是分配格.
定义 1.7[21]如果格L的子格I同时又是下集,则称I为格L的理想.对偶地,如果子格F同时又是上集,则称F为格L的滤子.
定理 1.1[21]设L为格,I是L的非空子集,则I为L的理想当且仅当I是下集且对并运算封闭.对偶地,设L为格,F是L的非空子集,则F为L的滤子当且仅当F是上集且对交运算封闭.
定义 1.8[23]设(X,≤)为偏序集,映射N:X→X,且∀a,b∈X,满足:
1)a≤b⟹N(b)≤N(a)(逆序对应),2)N(N(a))=a(对偶律或复原律),称N为X上的伪补或逆序对合算子或对合否算子,逆序对合算子也叫强否定算子.
定义 1.9[23]映射T:[0,1]×[0,1]→[0,1],如果∀a,b,c,d∈[0,1]满足条件:
1) 交换律T(a,b)=T(b,a);
2) 结合律T(T(a,b),c)=T(a,T(b,c));
3) 单调性a≤b,b≤c⟹T(a,b)≤T(c,d);
4) 边界条件T(1,a)=a;
则称T为[0,1]上的t-模.
定义 1.10[23]映射⊥:[0,1]×[0,1]→[0,1],如果∀a,b,c,d∈[0,1]满足条件:
1) 交换律⊥(a,b)=⊥(b,a);
2) 结合律⊥(⊥(a,b),c)=⊥(a,⊥(b,c));
3) 单调性a≤b,b≤c⟹⊥(a,b)≤⊥(c,d);
4) 边界条件⊥(a,0)=a;
则称⊥为[0,1]上的t-余模.
本文记t-模取小为⊗M,t-余模取大为⊕M,它们常称为Zadeh算子.
定义 1.11[24]若
而f在点x0无定义,或有定义但f(x0)≠A,则称x0为f的可去间断点.
定义 1.12[24]若函数f在点x0的左、右极限都存在,但
则称点x0为函数f的跳跃间断点.
可去间断点和跳跃间断点统称为第一类间断点,第一类间断点的特点是函数在该点处的左、右极限都存在.
定义 1.13[25]设M是(,∨,→)型代数,如果:
1)M上有偏序≤使(M,≤)成为有界分配格,且∨是关于序的上确界运算;
3) 对于任意的x,y,z∈M,以下条件成立:
(M1)x→y=y→x;
(M2) 1→x=x,x→x=1;
(M3)y→z≤(x→y)→(x→z);
(M4)x→(y→z)=y→(x→z);
(M5)x→y∨z=(x→y)∨(x→z),x→y∧z=(x→y)∧(x→z);
(M6) (x→y)∨((x→y)→x∨y)=1;
这里1是(M,≤)中的最大元,则称M为R0-代数.
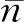
定义 1.14[26](模糊划分) 设U=[a,b]⊂R,U上的一个模糊划分指的是具有如下形式的对象:
其中
Ai={(x,uAi(x))|x∈U},i=1,2,…,n,函数
uAi:U→[0,1],i=1,2,…,n
定义了元素x∈U关于类Ai(代表某种质,即定性描述的类)的隶属度,并且满足下面的条件:
uAi(x0)=1;
uAi(x0)=1,那么uAi(x)在[a,x0]上不减,在[x0,b]上不增;
4) 对任意的x∈U,满足
0 若把上述定义中的条件4)替换为:对任意的x∈U,满足 基于模糊划分,下面给出模糊集合的公理化定义. 定义 1.15[26](公理化模糊集合) 设 uA(x)=uAi(x) 对所有x∈U都成立,那么 2) 如果uA(x)=1对所有x∈U都成立,那么 3) 如果 且r∈R+,那么 4) 如果 那么 5) 如果 那么 B1∩⊗B2∩⊗…∩⊗Bn∩⊗…= B1∪⊕B2∪⊕…∪⊕Bn∪⊕…= N(a)=1-a=aN. 同时为了方便,把 A={(x,uA(x))|x∈U} 要讨论模糊代数方程的可解性以及对其解集进行刻画,必然离不开与之紧密相连的模糊空间.因此,下面对模糊空间的序结构进行研究. A(x)≤B(x),那么称B包含A,或A被包含于B,并记为A⊆B或B⊇A;若任意 x∈U,A(x)=B(x),则称A与B相等,记为A=B. 证明若任意 则对任意x∈U都有 A(x)≤A(x)⊕MB(x)=(A∪⊕MB)(x) 且 B(x)≤A(x)⊕MB(x)=(A∪⊕MB)(x),那么A⊆A∪⊕MB且B⊆A∪⊕MB.因此,A∪⊕MB是{A,B}的上界. 若T是{A,B}的任一上界,则可知A⊆T且B⊆T,那么对任意x∈U都有 A(x)≤T(x) 且 B(x)≤T(x),从而 (A∪⊕MB)(x)=A(x)⊕MB(x)≤T(x). 因此 A∪⊕MB⊆T,故A∪⊕MB是{A,B}关于序⊆的上确界.对偶地,易证A∩⊗MB是关于序⊆的下确界,并且 关于序⊆的最大元与最小元,故 是有界格. 命题 2.1[19]设 则 (A∪⊕MB)∩⊗MC=(A∩⊗MC)∪⊕M(B∩⊗MC),(A∩⊗MB)∪⊕MC=(A∪⊕MC)∩⊗M(B∪⊕MC). 证明由定义1.15的5)以及命题2.1可知该结论成立. 其哈斯图如图1所示,且 图 1 例2.1运算1次的哈斯图 令 Fig. 2 Example 2.1 Haas diagram with two operations 注 2.1通过例2.1可知,当模糊划分中只有一个模糊集时,经过2次(r,R,N,∪⊕M,∩⊗M)运算生成的公理化模糊集合的全体是具有19个元素的格.若不对运算次数作限制,那么由一个模糊集生成的公理化模糊集合的全体是具有无限个元素的格. 定义 2.2定义映射 1)AN∪⊕MB⊆A→RB; 2)A⊆B→RC⟺B⊆A→RC; 6)A∩⊗MAN⊆B∪⊕MBN; 7)A→RC⊆(A→RB)∪⊕M(B→RC); 8)A∪⊕MB⊆((A→RB)→RB)∩⊗M((B→RA)→RA); 9) (A∪⊕MB)→RC=(A→RC)∩⊗M(B→RC),(A∩⊗MB)→RC=(A→RC)∪⊕M(B→RC); 10) 若B⊆C,则A→RB⊆A→RC,若A⊆C,则A→RC⊇B→RC; 11)A→RB⊆(A∩⊗MC)→R(B∩⊗MC),A→RB⊆(A∪⊕MC)→R(B∪⊕MC). 证明由推论2.1以及→R的定义易证结论成立. {∪⊕,∩⊗,→,r,N} 中的一些运算符号将公理化模糊集合连接而成的式子为模糊代数多项式. 仅含有一个未知变元的模糊代数方程称为一元模糊代数方程. 定义 3.3能使模糊代数方程左右两边相等的未知变元的取值称为模糊代数方程的解.由模糊代数方程所有解所组成的集合称为模糊代数方程的解集. A∪⊕MXr0=B, (1) A∩⊗MXr0=B. (2) 记 定理 3.11)S1≠∅当且仅当A⊆B; 证明1) 充分性 若A⊆B,则对任意x∈U都有A(x)≤B(x),那么有 必要性 若S1≠∅,则存在 使A∪⊕MXr0=B,即对任意x∈U有 (A∪⊕MXr0)(x)=A(x)⊕MXr0(x)=B(x),从而对任意x∈U有A(x)≤B(x),故A⊆B. 2) 当S1≠∅时,若X,Y∈S1,则A∪⊕MXr0=B且A∪⊕MYr0=B,由 (A∪⊕M(X∪⊕MY)r0)(x)= A(x)⊕M(Xr0(x)⊕MYr0(x))= A(x)⊕MA(x)⊕MXr0(x)⊕MYr0(x)= (A(x)⊕MXr0(x))⊕M(A(x)⊕MYr0(x))= B(x)⊕MB(x)=B(x),可知X∪⊕MY∈S1.由 (A∪⊕M(X∩⊗MY)r0)(x)= A(x)⊕M(Xr0(x)⊗MYr0(x))= (A(x)⊕MXr0(x))⊗M(A(x)⊕MYr0(x))= B(x)⊗MB(x)=B(x),可知X∩⊗MY∈S1,从而S1构成 的一个子格. 对任意 如果X⊆Z⊆Y,那么有 B=A∪⊕MXr0⊆A∪⊕MZr0⊆ A∪⊕MYr0=B,即 已知 求解A∪⊕MX2=B. 解由题可知 对任意x∈[0,2]有 B(x)=(A∪⊕MB)(x)= 因此,对任意x∈[0,2]有 A(x)≤B(x),即A⊆B,那么,由定理3.1知该方程有解并且 是该方程最大解. 显然有 又因为 所以 由 (A∪⊕M(X∩⊗MY)r0)(x)= A(x)⊕M(Xr0(x)⊗MYr0(x))= (A(x)⊕MXr0(x))⊗M(A(x)⊕MYr0(x))= 推论 3.2在方程(1)中,若A=B,则 根据以上结论,对于方程(2),对偶地可以得到下面的定理,其证明类似. 定理 3.21)S2≠∅当且仅当A⊇B; 推论 3.4在方程(2)中,若A=B,则 A→Xr0=B, (3) Xr0→A=B, (4) A→(B→Xr0)=C, (5) (A→Xr0)→B=C. (6) 记 定理 3.31)S3≠∅当且仅当B∪⊕MAN=B; 证明1) 必要性 若S3≠∅,则存在 使A→RXr0=B,即对任意x∈U有 B(x)=(A→RXr0)(x)=A(x)→RXr0(x)≥ AN(x)⊕MXr0(x)≥AN(x),那么AN⊆B,从而B∪⊕MAN=B. 充分性 若B∪⊕MAN=B,则 因为对任意x∈U有 (B→R(A→R(A→RBN)N))(x)= B(x)→R(A(x)→R(A(x)→RBN(x))N)= B(x)→R((A(x)→RBN(x))→RAN(x))= B(x)→R((B(x)→RAN(x))→RAN(x))= 所以B⊆A→R(A→RBN)N. 要证明A→R(A→RBN)N⊆B,即证明 (B→RAN)→RAN⊆B. 对任意x∈U有 ((B→RAN)→RAN)(x)= (B(x)→RAN(x))→RAN(x)≤ (BN(x)⊕MAN(x))→RAN(x)= (BN(x)⊕MAN(x))N⊕MAN(x)= (B(x)⊗MA(x))⊕MAN(x)= (B(x)⊕MAN(x))⊗M(A(x)⊕MAN(x))= B(x)⊗M(A(x)⊕MAN(x))≤B(x),那么 A→R(A→RBN)N⊆B,从而 A→R(A→RBN)N=B. 2) 若X,Y∈S3,则有A→RXr0=B且A→RYr0=B.因为对任意x∈U有 (A→R(X∩⊗MY)r0)(x)= (A(x)→R(X∩⊗MY)r0(x))= A(x)→R(Xr0(x)⊗MYr0(x))= (A(x)→RXr0(x))⊗M(A(x)→RYr0(x))= B(x)⊗MB(x)=B(x),所以X∩⊗MY∈S3.又因为 (A→R(X∪⊕MY)r0)(x)= A(x)→R(X∪⊕MY)r0(x)= A(x)→R(Xr0(x)⊕MYr0(x))= (A(x)→RXr0(x))⊕M(A(x)→RYr0(x))= B(x)⊕MB(x)=B(x),所以X∪⊕MY∈S3,从而S3构成 的一个子格. 另一方面,因为对任意x∈U有 (A→RXr0)(x)=B(x),那么 B(x)→R(A(x)→RXr0(x))= B(x)→R((Xr0(x))N→RAN(x))= (Xr0(x))N→R(B(x)→RAN(x))= (B(x)→RAN(x))N→RXr0(x)= (A(x)→RBN(x))N→RXr0(x)= ((A→RBN)N→RXr0)(x). 因此,(A→RBN)N⊆Xr0,即对任意x∈U有 3) 对任意X∈S3,任意x∈U有 B(x)=(A→RXr0)(x)=A(x)→RXr0(x)≥ (B∪⊕MA)(x)→RB(x)= (B(x)⊕MA(x))→RB(x)= (B(x)→RB(x))⊗M(A(x)→RB(x))= A→RX2=B. 解由题可知 则对任意x∈[0,2]有 B(x)≠(B∪⊕MAN)(x)= 由定理3.3可知该方程无解. A=A1∪⊕MA2∪⊕MA3,B=A2,求解A→RX2=B. 解由题可知 则对任意x∈[0,2]有 B(x)=(B∪⊕MAN)(x)= 因为 是该方程的最小解. 类似地,对于方程(4)~(6)可以得到下面的定理及推论,其证明相似. 定理 3.41)S4≠∅当且仅当B∪⊕MA=B; 定理 3.51)S5≠∅当且仅当 C∪⊕M(A→RBN)=C; 定理 3.61)S6≠∅当且仅当(C→RB)∪⊕MA=C→RB且B⊆C; 3) 对任意X∈S6均有 前面讨论了第1类关于∪⊕M和∩⊗M以及第2类关于蕴涵算子的模糊代数方程,下面讨论由第1类和第2类组合而成的模糊代数方程. A→(B∪⊕MXr0)=C, (7) A→(B∩⊗MXr0)=C, (8) (A∪⊕MXr0)→B=C, (9) (A∩⊗MXr0)→B=C. (10) 记 定理 3.71) 若S7≠∅,则C∪⊕MAN=C且B⊆C.当C∪⊕MAN=C且B⊆C时,如果 其中 证明1) 若S7≠∅,则存在 使A→R(B∪⊕MXr0)=C,也就是存在 使 B∪⊕MXr0=Y 且A→RY=C.由定理3.1和定理3.3容易得到 C∪⊕MAN=C 且B⊆C.当C∪⊕MAN=C且B⊆C时,如果 C(x)=(A→R(B∪⊕MXr0))(x)= A(x)→R(B∪⊕MXr0)(x)= A(x)→R(B(x)⊕MXr0(x))≥ 2) 由于A→R(B∪⊕MXr0)=C等价于 (A→RB)∪⊕M(A→RXr0)=C. B∪⊕MXr0=M 且A→RM=C,那么有 且 令 可知 因此 另一方面,有 是显然成立的,故 根据以上定理可类推方程,容易得到以下定理成立. 定理 3.81)S8≠∅当且仅当C∪⊕MAN=C且B⊇(A→RCN)N; 其中 定理 3.91)S9≠∅当且仅当B∪⊕MC=C且A⊆C→RB; 其中 定理 3.101) 若S10≠∅,则B∪⊕MC=C且CN⊆A.当B∪⊕MC=C且CN⊆A时,如果有 2) 当S10≠∅时,S10构成 的一个凸子格,并且 其中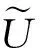
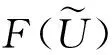

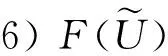

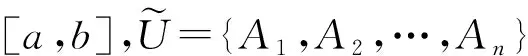

2 模糊空间的序结构
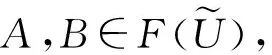
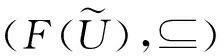
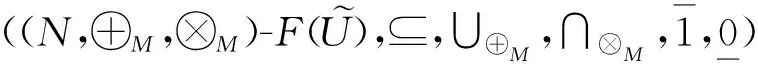

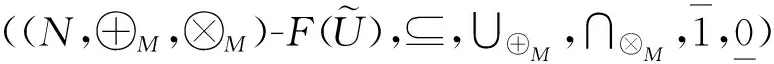
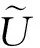
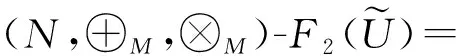
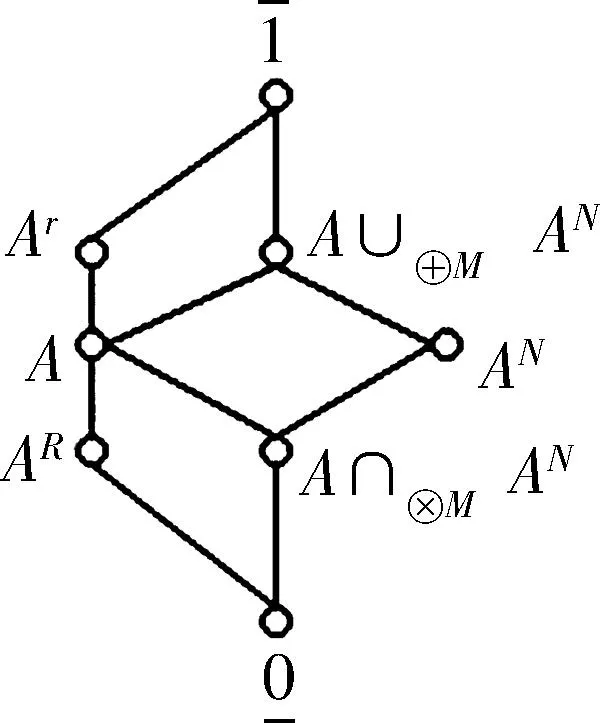

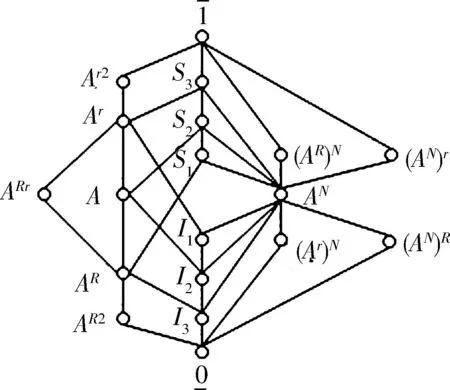
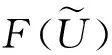
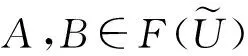
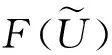

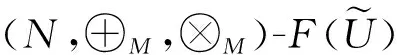

3 模糊代数方程
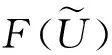
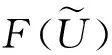

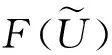
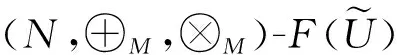
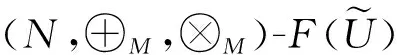


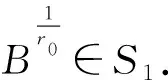
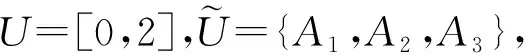
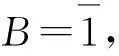
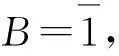




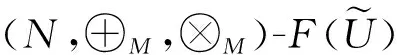
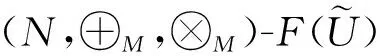
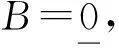
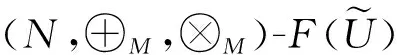
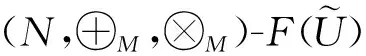
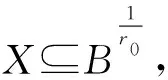
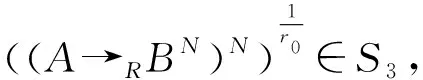
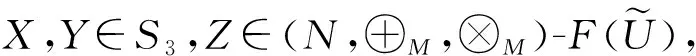

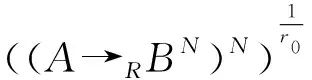

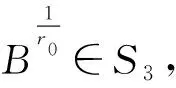
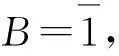
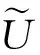
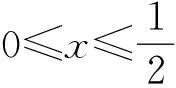
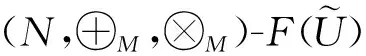
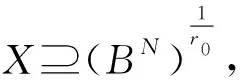
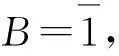

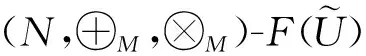

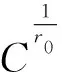
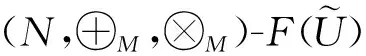
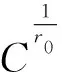

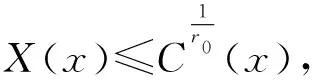

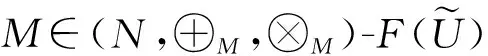
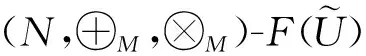
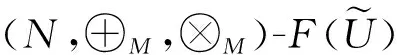
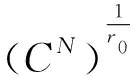
4 结束语

