偏序集上的弱Scott拓扑与弱测度拓扑

王 武, 李旭东

(天津理工大学 中环信息学院, 天津 300380)

Domain理论[1]属于格论、拓扑学、范畴论及理论计算机科学的交叉领域,目前已经发展为数学与理论计算机的一个重要分支.Domain理论的提出源于2个不同的背景:理论计算机中函数式语言的语义研究和偏序结构与内蕴拓扑的纯数学研究[2-4].为了将domain理论进行推广,许多学者[5-6]在一般的偏序集上定义了连续和拟连续结构,并不断向信息科学、逻辑学、分析学及各种应用学科渗透,得到了很多有意义的数学模型,为计算机高级程序设计语言提供了数学模型.2000年,Martin[7]在研究计算问题的数学基础时,于连续dcpo(即domain)上引入了μ拓扑,证明了这种内蕴拓扑实际上是由domain上具有一定条件的测度所诱导的.文献[8]在一般的偏序集上引入了测度拓扑和全测度的概念,同时讨论了连续偏序集上的测度拓扑和全测度的性质.文献[9-11]广泛研究了偏序集上的s2连续性,并得到了很多有意义的结论.本文在此基础上进一步探讨s2连续偏序集以及弱Scott拓扑的一些性质,定义了弱测度拓扑,并研究了弱测度拓扑与其它内蕴拓扑间的关系,利用测度拓扑刻画了偏序集的s2交连续性,同时研究了弱Scott拓扑的连通性.这一工作提供了认识偏序集连续性的一个新方向,有助于偏序集理论的研究.

1 预备知识

首先介绍偏序集的一些基本概念[12].设L为偏序集,任给A⊆L,记

↑A={x∈L:∃a∈A,a≤x},↓A={x∈L:∃a∈A,x≤a}.

若A为单点集{a},则记↑A=↑a,↓A=↓a.如果↑A=A,则称A为上集;同理可定义下集.用A↑与A↓分别表示A的所有上界和所有下界的集合.令Aδ=(A↑)↓,称Aδ为A的正规完备化算子,显然Aδ为下集,令δ(L)={Aδ:A⊆L}.设L为偏序集,任给x,y∈L,如果对任意定向集D⊆L,y∈Dδ意味着D∩↑x≠∅,则称x逼近y,记为x≪y.记

x={y:x≪y},x={y:y≪x},K(L)={x∈L:x≪x}.

定义 1.1[12]设L为偏序集,w(L)为L的所有非空有限子集的集合:

1) 若任意x∈L,定向集D⊆L,x∈Dδ蕴含x∈clσ2(D∩↓x),则称L为s2交连续偏序集;

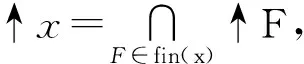
命题 1.1[12]设L为偏序集,则L是s2连续偏序集当且仅当L是s2拟连续的和s2交连续的.

设L为偏序集,任给子集U⊆L,如果U=↑U且对任意的定向子集D⊆L,Dδ∩U≠∅意味着D∩U≠∅,则称U为σ2开集.所有的σ2开集构成一个拓扑,称为弱Scott拓扑[12],记为σ2(L).设L为偏序集,则L的所有上集构成一个集合,称为Alexandrov拓扑,记为α(L).对偶地,L的全体下集形成的拓扑,称为对偶Alexandrov拓扑,记为α*(L).以{L↓x:x∈L}为开子基形成的拓扑称为下拓扑,记为ω(L);称σ2拓扑与下拓扑的共同加细λ2(L)=ω(L)∨σ2(L)为弱Lawson拓扑.

命题 1.2[12]设L为偏序集,则:

1) 如果L是s2连续偏序集,则{x:x∈L}为弱Scott拓扑的基;

2) 如果L是s2拟连续偏序集,令F={x:F≪x},则{F:F∈w(L)}为弱Scott拓扑的基.

定义 1.2设L为偏序集,B⊆L,若x∈L,∃Bx⊆B∩x,使Bx是定向集且x∈(Bx)δ,则称B为L的基.

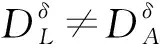
命题 1.3[13]设P、Q为偏序集,f:P→Q,则f是σ2连续的,即f:(P,σ2(P))→(P,σ2(Q))连续当且仅当任意定向集D⊆P,f(Dδ)⊆(f(D))δ.

定义 1.3[14]设X为拓扑空间,如果X中不存在2个非空闭集A、B使A∪B=X且A∩B=∅,则称X是连通空间.如果X的子集A作为子空间是连通空间,则称A是X的连通子集.

众所周知,拓扑空间X是连通空间当且仅当X中不存在2个非空开集A、B使得A∪B=X且A∩B=∅.

定义 1.4[15]设L为偏序集:

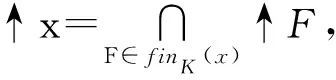
命题 1.4[15]设L为s2代数偏序集,任意x,y∈L,x≪y,则存在k∈K(L)使得x≤k≤y.

2 s2连续偏序集的伴随性质

定义 2.1[16]设P、Q为偏序集,g:P→Q,d:Q→P,若g、d都是保序的,且x∈P,y∈Q,g(x)≥y当且仅当x≥d(y),则称映射(g,d)为P,Q间的伴随,此时称g为d的上伴随,d为g的下伴随.

易知(g,d)为P,Q间的一个伴随当且仅当d∘g≤1P,g∘d≥1Q.

命题 2.1设P、Q是s2连续偏序集,映射(g,d)为P、Q间的一个伴随,则下列等价:

1) g是σ2连续的;

2) U∈σ2(Q),↑d(U)∈σ2(P);

3) x,y∈Q,若x≪y,则d(x)≪d(y).

证明1)⟹2) 如果x∈↑d(U),则存在u∈U使得x≥d(u),则g(x)≥u.由U∈σ2(Q)知存在u′∈U使得u′≪u≤g(x),所以u′≪g(x).设D⊆P是定向集,且dg(x)∈Dδ.由于g是σ2连续的,则g(Dδ)⊆(g(D))δ,即gdg(x)∈g(Dδ)⊆(g(D))δ.由g∘d≥1Q知g(x)≤gdg(x),则g(x)∈(g(D))δ.因为u′≪g(x),则存在d∈D使得u′≤g(d).而d(u′)≤dg(d)≤d,d(u′)≪dg(x)≤x,即d(u′)≪x.则任意x∈↑d(U)∈σ2(P),存在d(u′)∈↑d(U)使得d(u′)≪x,所以↑d(U)∈σ2(P).

2)⟹1) 任意U∈σ2(Q),若证g是σ2连续的,只需证g-1(U)∈σ2(P).下证g-1(U)=↑d(U).任意x∈g-1(U),则g(x)∈U,则存在u∈U使得u≪g(x),则d(u)≤x,因此x∈↑d(U).反之,任意x′∈↑d(U),存在u′∈U使d(u′)≤x′,则u′≤g(x′),而U是上集,所以g(x′)∈U,x′∈g-1(U)．因此g-1(U)=↑d(U),从而g是σ2连续的.

1)⟹3) 设x,y∈Q,若x≪y.设D⊆P为定向集,d(y)∈Dδ.由g为σ2连续的,则g(Dδ)⊆(g(D))δ.又y≤gd(y),则x≪gd(y),因此存在d∈D使得x≤g(d),则d(x)≤dg(d)≤d,所以d(x)≪d(y).

3)⟹1) 任意U∈σ2(Q),若证g是σ2连续的,只需证g-1(U)∈σ2(P).事实上,任意x∈g-1(U),g(x)∈U,由s2连续知存在u∈U使得u≪g(x),则d(u)≪dg(x)≤x,而gd(u)≥u∈U,因此d(u)∈g-1(U),则x∈d(u)∈g-1(U),则g-1(U)∈σ2(P),g是σ2连续的.

命题 2.2设P、Q是s2连续偏序集,映射d:Q→P是保序的:

1) x,y∈Q,若x≪y,则d(x)≪d(y);

2) d(K(Q))⊆K(P),则1)⟹2),如果Q是s2代数连续的,则1)与2)等价.

证明1)⟹2) 显然成立;

2)⟹1) 如果Q是s2代数连续的,设x,y∈Q,x≪y,由Q是s2代数的,存在k∈K(Q)使得x≤k≤y,又d(k)∈K(P),则d(x)≪d(y).

推论 2.1设P是s2连续偏序集,Q是s2代数连续的,映射(g,d)为P,Q间的一个伴随,则下列等价:

1) g是σ2连续的;

2) U∈σ2(Q),↑d(U)∈σ2(P);

3) x,y∈Q,若x≪y,则d(x)≪d(y);

4) d(K(Q))⊆K(P).

3 弱测度拓扑

3.1 s2连续偏序集与弱测度拓扑

定义 3.1称偏序集L上的σ2拓扑和对偶Alexandrov拓扑的共同加细α*(L)∨σ2(L)为L上的弱测度拓扑,记为μ2(L).

由定义显然有弱Lawson拓扑粗于弱测度拓扑,即有σ2(L)⊆λ2(L)⊆μ2(L).

命题 3.1设L是s2连续偏序集,则B={x∩↓y:x,y∈L}是μ2(L)的一个基.

证明因为x和↓y分别是σ2拓扑和对偶Alexandrov拓扑中的开集,则B⊆μ2(L).而{x:x∈L}和{↓y:y∈L}分别是σ2拓扑和对偶Alexandrov拓扑的基,故μ2(L)有子基{x:x∈L}∪{↓y:y∈L}.而x∈U∈μ2(L),则存在有限集E,F⊆L使得x∈(∩e∈Ee)∩(∩f∈F↓f)⊆U.从而e≪x≤f对任意的e∈E,f∈F都成立.由L的s2连续得知x定向,从而存在z∈x使得任意e∈E,e≤z≪x.于是有z∩↓x∈B且x∈z∩↓x⊆U,这说明B是μ2(L)的基.

命题 3.2设L是s2连续偏序集,U∈σ2(L),W为下集,则↑(U∩W)∈σ2(L).

证明设D是L的定向子集,且Dδ∩↑(U∩W)≠∅,令d∈Dδ∩↑(U∩W)≠∅,则存在x∈U∩W使得x≤d,则x∈Dδ.由L是s2连续且U∈σ2(L),存在t∈U使t≪x≤d.于是由x∈Dδ和t≪x知存在d′∈D∩↑t.再由x∈W和W为下集知t∈W,即t∈U∩W.于是d′∈D∩↑(U∩W).由σ2开集的定义知↑(U∩W)∈σ2(L).

命题 3.3设L是s2连续偏序集,则下列成立:

1) 若U∈μ2(L),则↑U∈σ2(L).进一步地,如果U是上集,则U∈μ2(L)当且仅当U∈σ2(L);

2) x∈L是紧元当且仅当{x}∈μ2(L);

3) 若A⊆L是上集,intσ(A)=intλ(A)=intμ(A);

4) 若B⊆L是下集,则clσ(A)=clλ(A)=clμ(A).

证明1) 设U∈μ2(L),t∈↑U.不妨设u≤t,u∈U,则存在x,y∈L使得u∈x∩↓y⊆U,则t∈↑(x∩↓y).由命题3.2知↑(x∩↓y)∈σ2(L),这说明在σ2拓扑中,t为↑U的内点.由t∈↑U的任意性知↑U中的点都是内点,则↑U∈σ2(L).如果U是上集,显然U∈μ2(L)当且仅当U∈σ2(L).

3) 设A⊆L是上集.由σ2(L)⊆λ2(L)⊆μ2(L)知intσ(A)⊆intλ(A)⊆intμ(A).因为intμ(A)⊆↑intμ(A)⊆↑A=A且由1)得↑intμ(A)∈σ2(L),则intσ(A)⊇intμ(A).从而有intσ(A)=intλ(A)=intμ(A).

4) 由3)知显然.

易知如果U为弱测度拓扑中的闭集,则↓U对定向集的正规完备算子一般不封闭.

3.2 s2交连续偏序集与弱测度拓扑偏序集的s2连续性可以保证弱测度拓扑的很多性质,但弱测度拓扑并不能用来刻画s2连续偏序集.事实上,弱测度拓扑与s2交连续偏序集息息相关.下一定理表明,利用偏序集上的弱测度拓扑可以刻画s2交连续性.

定理 3.1设L是偏序集,则下列条件等价:

1) L是交连续偏序集;

2) U∈σ2(L),x∈L,则↑(U∩↓x)∈σ2(L);

3) U∈σ2(L),A为下集,↑(U∩A)∈σ2(L);

4) U∈μ2(L),有↑U∈σ2(L).

证明1)⟺2) 由文献[9]中引理4.2可得.

2)⟹3) 设U∈σ2(L),A为下集,则

3)⟹4) 设U∈μ2(L),任意t∈↑U,则存在u∈U,u≤t.由U∈μ2(L)知存在V∈σ2(L)以及下集A使得u∈V∩A⊆U,t∈↑(V∩A).由已知可知↑(V∩A)∈σ2(L),则在σ2拓扑下,t是↑U的内点.由任意性知↑U∈σ2(L).

4)⟹2) 设U∈σ2(L),x∈L,有(U∩↓x)∈μ2(L),则↑(U∩↓x)∈σ2(L).

命题 3.4设L是s2拟连续偏序集,则B={F∩↓y:F∈w(L),y∈L}是μ2(L)的基.

证明与命题3.1类似,不再赘述.

命题 3.5设L是偏序集,则下列等价:

1) L是s2连续偏序集;

2) L是s2拟连续偏序集且如果U∈σ2(L),A为下集,↑(U∩A)∈σ2(L);

3) L是s2拟连续偏序集且如果U∈μ2(L),有↑U∈σ2(L).

4 σ2拓扑的连通性

定义 4.1[17]设L为偏序集,x∈L:

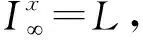
命题 4.1[17]设L是偏序集,则L不序连通当且仅当存在L的2个非空子集A、B使得A∪B=L,A∩B=∅且A、B既是上集又是下集.

命题 4.2设L是偏序集,则L为序连通的当且仅当(L,σ2(L))连通.

证明设(L,σ2(L))是连通的,用反证法.若L不序连通,由命题4.1得L中存在2个非空子集A、B使得A∪B=L,A∩B=∅且A、B既是上集又是下集.此时,对A中任一定向集D,由于A既是上集又是下集,则Dδ⊆A时,故A是σ2闭集.同理A是σ2闭集,这样便得(L,σ2(L))不连通,矛盾,则L为序连通.反之,设L为序连通的,假设(L,σ2(L))不是连通的,则存在2个非空开集A、B使A∪B=X且A∩B=∅,则A、B均是上集.设x∈A,y≤x,如果y∈A,则y∈B,由B为上集知x∈B,与x∈A矛盾,故A为下集.同理B为下集.与L为序连通的矛盾,故(L,σ2(L))是连通的.

推论 4.1设L是偏序集,若(L,σ2(L))连通,则空间(L,λ2(L)),(L,μ2(L))均连通.

致谢2021年高等学校大学数学教学研究与发展中心教学改革项目(CMC20210115)对本文给予了资助,谨致谢意.