立体式教学模式的研究与实践——以《实变函数》课程为例

文 斌 刘春妍 康兆敏

（佳木斯大学理学院 黑龙江佳木斯 154007）

目前，高等师范院校大学生就业难与用人单位“人才”难觅的悖论促使高等教育工作者不得不深思：如何立足专业课程体系改革教学方法、创新教学模式、适时更新教学内容，培养出适应社会需求的高层次人才。为适应大类招生的需要，根据多年的教学管理与实践，笔者从创新教学模式入手，在我校数学与应用数学本科专业的课程教学中进行大胆的探索与研究，以《实变函数》这门公认的数学专业课程体系中既难教又难学的课程为例，通过2005-2008级等四届学生的教学实践与效果反馈，在激发学生的学习兴趣，增强其独立思考问题、分析问题与解决问题的能力方面有所体悟。

《实变函数》是高等院校数学本科专业学生的一门重要的专业课程。它是《数学分析》的延续和发展，是现代数学各个分支的基础之一；它的任务是使学生掌握近代抽象分析的基本思想，系统掌握Lebesgue测度与积分理论，着重培养学生的思维能力和逻辑推理能力。其中的Lebesgue测度与积分理论已经成为数学工作者的基础知识。然而，由于该课程概念性强、内容抽象、推理严谨，在学术界一直被公认为是数学专业课程体系中的兼教师难教与学生难学为一体的课程之一。

一、立体式教学模式的涵义

立体式教学是新形势下的一种全新的教学方式，它是在教学活动中能使学生的认知过程、情感过程和意志过程等得到协调发展的一种教学方法。立体式教学模式不仅仅是现代化教学手段的变革，还是教育观念的变革，教育理论的变革，对教育模式和教育体系的改革具有积极的作用。本文的立体式教学模式是指针对学生的情况和所讲授课程的内容设计出立体的网络结构，交叉运用多种教学手段和辅助设备，使学生有目的、感兴趣、自觉地完成问题的发现和解决，并通过教学反馈及时完善的一种教学模式，强调“学生学习主动化、资源整合多元化、课程讲授多样化、学习支持立体化”。

二、立体式教学模式的实践探索

（一）立体化夯实课程基础

通过多媒体课件形象生动地展现本门课程创立的主要过程：首先介绍本门课程的起源和主要创始人创立本课程的目的、简单过程及其主要成果；同时建立其与其它课程的联系，使学生了解本课程的研究目的和发展过程，消除其对新课的陌生感。《实变函数》是十九世纪末、二十世纪初，主要由法国数学家Lebesgue创立的。它是普通微积分学的继续。Lebesgue针对Riemann可积暴露出的一些不足创立了Lebesgue测度和积分。Riemann积分的不足主要表现为以下两个方面：其一，Riemann意义下可积函数类太小。只有具有限个不连续点或个别具有可数多个不连续点的函数 （例如区间 [0,1]上的 Riemann函数）是Riemann可积的，而许多形式非常简单的函数，例如[0,1]上的Dirichlet函数都不可积这一不足；其二，有些条件过于严格，影响了Riemann积分的实践应用。例如，积分与极限运算交换次序的条件过于严格。在《数学分析》中我们知道【2】，要求函数列在区间上一致收敛于fn(x)，每一fn(x)都在[a,b]上连续，才有这样通过铺设问题环境，激发学生的学习兴趣。

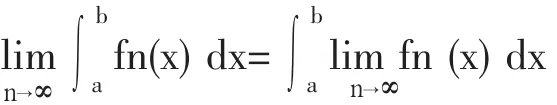
（二）立体化搭建知识框架

布鲁纳总结出的四个数学学习原理，其中关联原理是指应把各种概念、原理联系起来，在同一的系统中学习。我们首先通过一个实例弄清本门课程的研究思路：根据函数Riemann积分存在的一个充要条件，即若函数f(x)在[a,b]上有界，在[a,b]上插入分点 a=x0＜x1＜ …＜xn-1xn＝b

把[a,b]分成 n 和小区间[xi-1,xi](i＝1,2…，n)，记

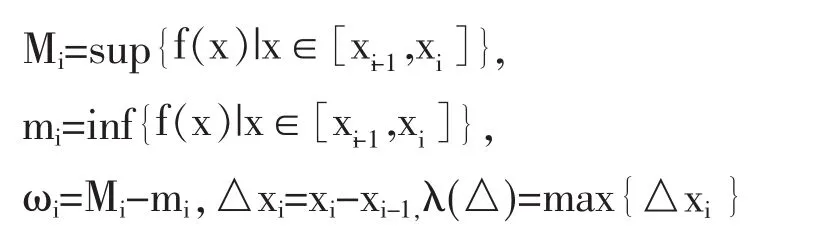
有

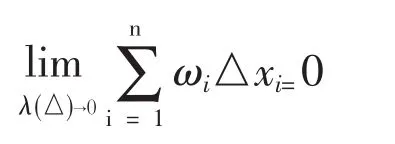
可知Dirichlet函数：

在任意区间上的振幅，从而对于积分区间[0,1]上的任何Riemann定义下的分划后所求得的振幅和得到此函数Riemann不可积。究其原因可能是出在Riemann积分中对于积分区域的分划要求过于狭隘。如果根据Dirichlet函数在有理点取1，无理点取0这一特点把积分区间[0,1]简单的分划成两个集合：E1={[0,1]上的有理数}和E2={[0,1]上的无理数}，则函数在这两个集合上的振幅和就满足可积的条件了。据此我们是否可以考虑定义一个新的积分，通过分划被积函数的值域：m=y0＜y1＜…yn-1＜yn＝M，令 Ek=E[yk-1≤f≤yk](k=1,2,…n)则振幅和变成（yk-yk-1）·mEk，其中表示的测度（现可简单理解为一种“长度”）。由于此时的不再是简单的区间。这提示我们应当首先要研究一般集合的性质及其何时存在测度。这应该看成是《实变函数》的第一、二部分内容——集合论和测度论（包括集合的测度和函数的测度）。接下来研究满足什么要求的函数才可积，即《实变函数》的第三部分内容——积分论。这三个板块都是后者以前者为基础，环环紧扣。以大家熟悉的集合知识为起点，以我们熟知的Riemann可积函数为基础，由浅入深，符合学生的认知规律。

（三）立体化设计教学环节

结合所讲授内容的实际，选定不同的教学方法，激发学生的学习兴趣，逐步训练和培养学生的创新能力。特别注意以下教学环节的运用。

1.重视有助于独立思考与合作的自学

自20世纪50年代中期以来，数学家华罗庚曾多次倡导“要学会自学”、“要学会读书”，他认为“学生在校学习期间，学会读书与学得必要的专业知识是同等重要的。学会读书不但保证我们在校学习好，而且保证我们将来永远不断地提高”。布置自学内容，学生利用课外时间研读和小组内讨论，最后在课堂上由小组选派代表进行讲解。讲授期间允许提问和讨论。通过学生的讲解和讨论，充分锻炼学生积极思考、发现问题、独立和合作解决问题的能力。

2.引入有助于知识理解与应用的史料

通过多媒体课件展示、提供相关的网址或链接，介绍部分定理或定义的产生背景和耐人寻味的实际应用背景。史料的引入使学生体会到《实变函数》这门课程在整个学科课程体系中的地位和作用，同时也让学生经历了一个科学家发现问题并解决问题的过程。通过潜移默化的熏陶，启迪学生的科学思维方法，培养学生探索新知识的意识和掌握独立解决问题的能力。

3.布置有助于知识拓展的课后思考题

在数学教学中，学生受本身知识结构、思维定势以及知识点的难易程度、周围环境的干扰等因素的影响，对某些知识点可能不能当堂领会。作为课堂教学的补充与深化，教师有针对性的布置课后思考题。这样做既能加深学生对知识点的理解与掌握，又能锻炼学生独立思考和创新能力，同时对激发学生的求知欲，完成学生发现学习【3】的过程。例如，在研究 Cantor集【4】的基数（或称势）时，学生往往因为对此集合所包含元素了解不够全面，会产生只包含分点（k/3n，其中n为正整数，k为小于3n的某些正整数）的错觉。让学生在课后根据Cantor集是闭集这一性质，设法找到分点以外的点（如1/4等）。引发学生的探索和创造灵感。

4.强化有助于知识融会贯通的小结

在完成一章的学习后，要求每一名学生写出本章小结。要求以最简洁的语言列出本章所学到的主要内容；用自己的语言说明定理；掌握本章的重点及其与以上章节内容之间的联系。通过学生自我将本章内容化繁为简，锻炼其学会动脑和动手。在全部完成本课程的讲授时，要求学生根据每章内容之间的关系绘出一个交叉网络图，使学生将全部知识融会贯通，减轻学生期末复习的压力。

三、校验教学效果

通过教学反馈可以校验课程的教学效果，我们通过多种方式、多种途径对教学效果进行全方位收集与分析总结。

（一）教师可以通过课堂上观察学生的身体反应（主要是面部反应）和提问来了解学生对每个问题的掌握情况。课后及时将针对某个知识点好的教学手段（或方法）和没收到预期效果的知识点记录下来，设法通过以后章节的教学弥补不足。

（二）通过定期的调查问卷及时掌握教师在每个章节教学进度的快慢、学生的理解程度和学生自主学习遇到的困难。

（三）通过期末考试了解绝大多数学生经过本门课程的学习后的整体掌握情况和出现问题的知识点（或章节）。

（四）考研与工作中，这些第一手材料都是下一轮教学的重要参考资料，经过几轮的修订与尝试不断完善我们的教学。

尽管我们对立体式教学模式进行了初步的实践探索与研究，但随着学生自身状况与社会现实需求的不断变化，对教学模式的研究也将永无止境。“不积跬步，无以至千里；不积小流，无以成江河”，我们将继续对立体式教学模式进行深入研究与推广，力争培养出适应时代需求的高层次专业人才。

[1]周兴和，叶惟寅.实践中的好课与好课的实践，[J].数学教育学报，2005，（2）：80-82.

[2]复旦大学数学系，陈传璋等.数学分析（下册）[M].高等教育出版社，2004,70-71.

[3]郑君文，张恩华.数学学习论[M].广西教育出版社，1996,27-28.

[4]周民强.实变函数论[M].北京大学出版社，2001,55-57.