Poles of L-Functions on Quaternion Groups

Çetin RTŞ

1 Introduction

In the theory of automorphic forms,Eisenstein series andL-functions play critical roles.The analytic continuation ofL-functions and information about the poles can be obtained by using Siegel Eisenstein series.To be able to get better results for location of poles,one needs to use the doubling method and the regularized Kudla-Rallis-Siegel-Weil formula.Poles ofL-functions are important in the theory of theta correspondence.In this paper,we follow Kudla-Rallis’work on the orthogonal-symplectic case to have similar results for quaternion groupsO∗(4n)andSp∗(n,n).Here some Yamana’s results on quaternion groups are crucial.

Let k be a totally real number field and letDbe a quaternion division algebra over k with a main involutionσ.Letbe either 1 or−1.LetV=Dmbe a non-degenerate-Hermitian space equipped with aD-valued non-degenerate form(,)such that(x,y)σ=−(y,x)and(xa,yb)=aσ(x,y)bfor alla,b∈Dandx,y∈V.Assume thatmis even.Let

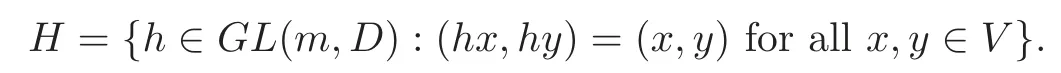
LetW′be a 2n-dimensional vector space overD.LetWbe a maximal totally isotropic subspace ofW′.LetS∈GL(2n,D)satisfyS∗=S,whereS∗=tSσis the conjugate transpose ofS.Sdefines an-Hermitian form onW′.Let

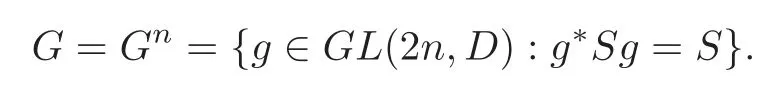
ThenGandHform a dual reductive pair in the sense of[5].We can see these groups as quaternion orthogonal or symplectic groups.For example,Gcan be denoted as follows:

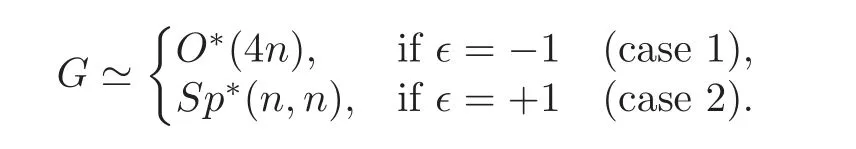
LetPbe the parabolic subgroup ofGwhich stablizes a maximal isotropic subspace ofW′.Such a parabolic subgroup is called a Siegel parabolic subgroup and it has the Levi decompositionP=MN,where

is the standard Levi subgroup and

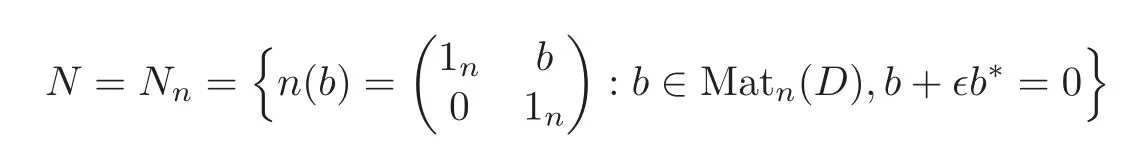
is the unipotent radical.

The modular function ofPis given bywith

where

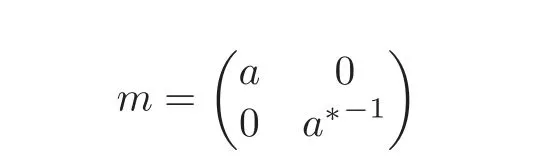
is in the standard Levi component ofP.

Fix a non-trivial additive characterψon A/k.LetSbe the space of Schwartz functions onVn(A).Letω=ωψbe the associated Weil representation ofG(A)×H(A)onS(Vn(A))(for the explicit definition see[9,13]).

Forgands∈C,we define the function

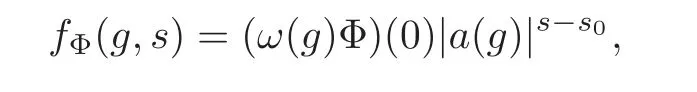
wheres0=m−

For a unitary idele-class characterχ:let

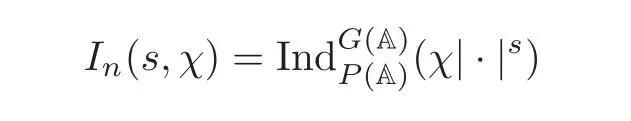
be the degenerate principal series representation ofG(A)consisting of functionsfonG(A)which are finite sums of monomialswhere at any archimedeanv,and smooth,and at any non-archimedeanv,fvis locally constant and compactly supported,such that

Note that the mapdefines aintertwining map fromto

We fix a standard maximal compact subgroupK=ofG(A).ThenI(s,χ)is a representation ofwhereis the Lie algebra ofA function

is called a standard section if the restriction of Φ(s)toKis independent ofs.

For a standard section Φ(s)∈In(s,χ)andg∈G(A),we define an Eisenstein series

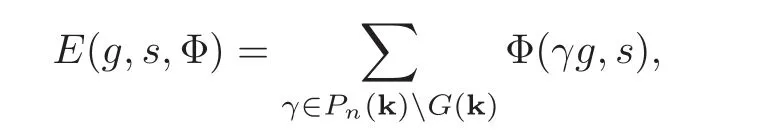
which is absolutely convergent for Re(s)Eisenstein series may have a pole when Re(s)≤ρ2n.Now we define the normalized Siegel Eisenstein series by

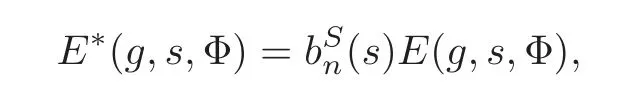
whereis a certain product of AbelianL-series for a finite set of primesSwhich includes bad primes(see Lemma 2.1).

Suppose thatπis a given irreducible cuspidal representation ofG(A)andχwas a given character ofLet

be the(partial)standard LanglandsL-function associated toπ⊗χ.An integral representation of thisL-function was given in[9]by using a doubling method.

Define the setto be

Theorem 1.1(Main Theorem) (1)π⊗χ)is entire.

(2)If χ2=1,thenhas at most simple poles and these can only occur for

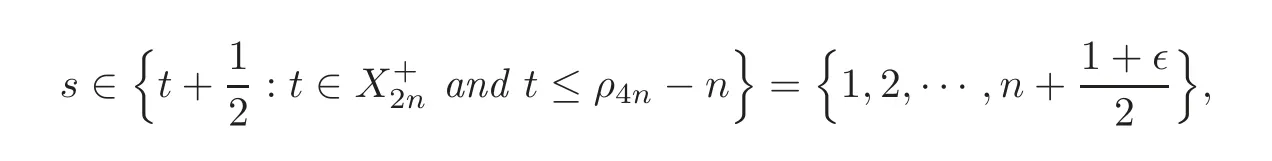
where s=2is not included in the set when

The proof uses the information about the poles of normalized Siegel Eisenstein series,the regularized Kudla-Rallis-Siegel-Weil(KRSW for short)formula and the doubling method.

2 Poles of Normalized Siegel Eisenstein Series

For Re(s)＞ρ2ndefine an intertwining operatorM(s,χ)=Mn(s,χ),

by

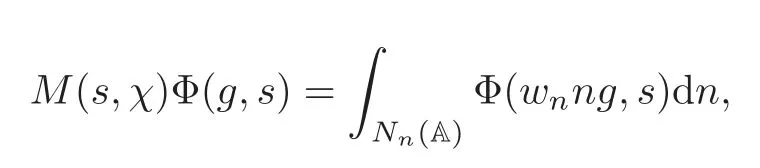
wherewnis the longest Weyl element

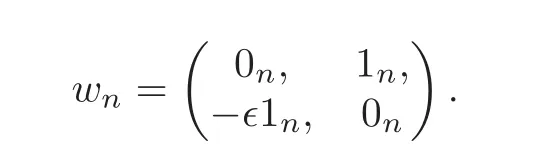
From the general theory of Eisenstein series(for example see[1,8]),we have the following theorem.

Theorem 2.1The Eisenstein series E(g,s,Φ)is absolutely convergent in the half-planeRe(s)＞ρ2nand has a meromorphic continuation to the complex plane.Its meromorphic continuation satisfies the functional equation

Note thatM(s,χ)has a meromorphic continuation as well.

For any non-archimedean placevof k at whichχvis unramified,letbe the spherical standard section of

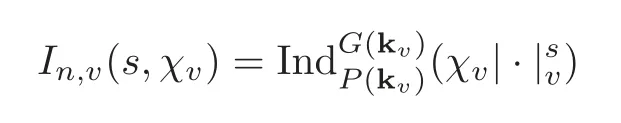
determined by=1 for allk∈Kv.SinceIn(s,χ)=we can write

where,for

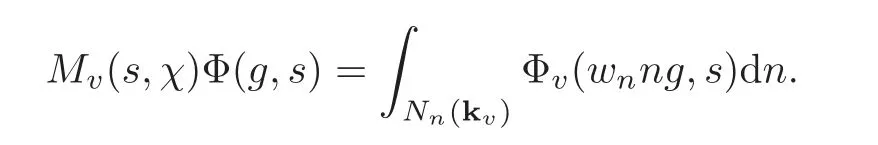
The following calculation can be done by using a standard Gindikin-Karpelevich type argument(see[4])or a Casselman type argument(see[2,Theorem 3.1,p.397]).

Lemma 2.1If v is a non-archimedean place ofkat which χvis unramified and D splits overkv,then

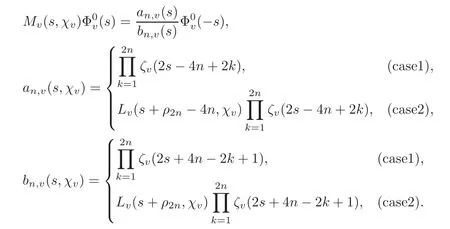
Theorem 2.2(see[13])LetΦ(s)be a holomorphic section of In(s,χ).

(1)Ifthen E∗(g,s,Φ)is entire.

(2)Assume that χ2=1.Then the poles of E∗(g,s,Φ)inRe(s)≥0are at most simple and occur in the set

Remark 2.1Kudla and Rallis investigated the poles of the normalized Eisenstein series for orthogonal and symplectic groups in[6–7].In[10]similar results are obtained for quaternion groups,where some possible poles on the left half-plane are not ruled out.By using a regularized Siegel-Weil formula for quaternion groups,Yamana were able to remove possible poles on the left-half plane in[13].

3 Regularized Kudla-Rallis-Siegel-Weil Formula

For Φ∈S(V(A)n),g∈GAandh∈HA,define a theta kernel:

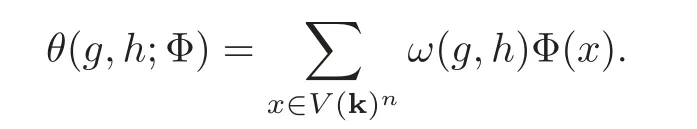
This is a smooth function on-invariant,and slowly increasing on By Weil’s criterion(see[11,13]),the integral

converges absolutely for all Φ if eitherr=0 orm−r＞whereris the dimension of a maximal isotropic k-subspace ofV.

Assume thatr＞0 andm−rThe theta integral is not convergent anymore for all Φ.We need to have a regularization.From[7]and[13],one can regularize the theta integral by finding an elementz0in the Bernstein center ofHsuch that for all Φ

(1)= Φ(0),

(2)=0.

Here a local placevis fixed andFis defined to be a certain localGv×Hv-intertwining map fromS(Vn)to a local induced representation(see[13]).

From the construction,it can be seen that the kernelθ(g,h;z0Φ)is rapidly decreasing onH(k)H(A)and the integral

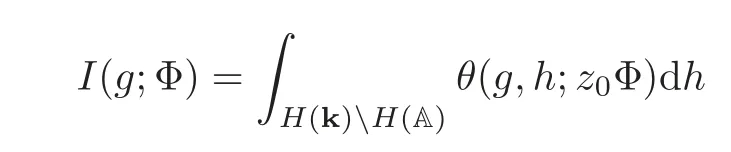
is independent of the choice of a local placevandz0.

Now we can state a regularized SWKR-formula for quaternion groups.

Theorem 3.1(see[13])LetΦbe a holomorphic section of I(s,χ),s0=m−ρ2nand A−1(g,Φ)=0

(1)Let=−1.Then we have

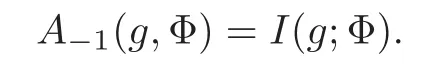
(2)Let=1.

(a)If m≤n,then

(b)If m≥n+1,then for every j

where Ij(g;Φ)s denote to the theta integrals associated to the global equivalence classes locally isometric to V.

4 Poles of L-Functions

4.1 Zeta integrals of doubling method

Letπ=be an irreducible automorphic cuspidal representation ofG(A).The Peterson pairing

induces a pairing onπand we choose local pairings〈,〉onπvsuch that

wherefi=fori=1,2 are factorizable vectors.Here,local pairings are normalized so that=1 for the spherical vector

The productG×Gis embedded inas usual by

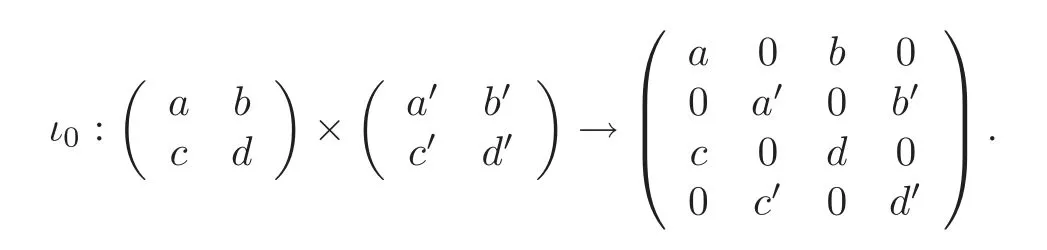
We make a slight change inι0to make it useful.Set

Let

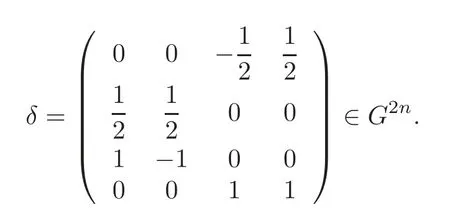
Choosef1,f2∈πsuch thatis a spherical vector,that isKv-invariant for allv/∈S.Choose a factorizable section

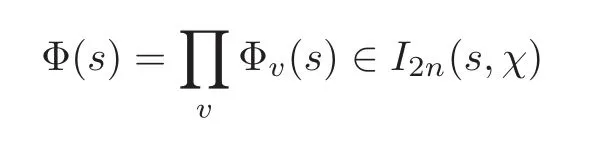
such that for allv/S,Φv(s)is the normalized spherical vector.LetE(g,s,Φ)be the Siegel Eisenstein series on(A).Consider the zeta integral

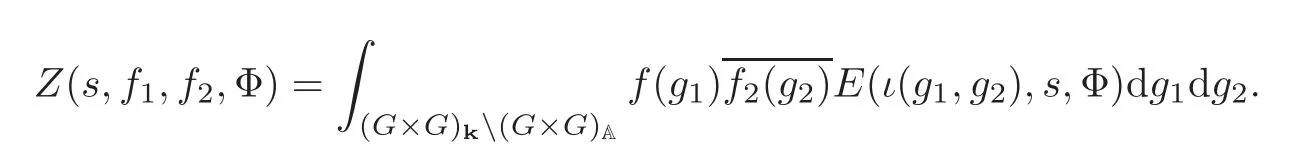
From the doubling method of[3–4],we have that for Re(s)＞

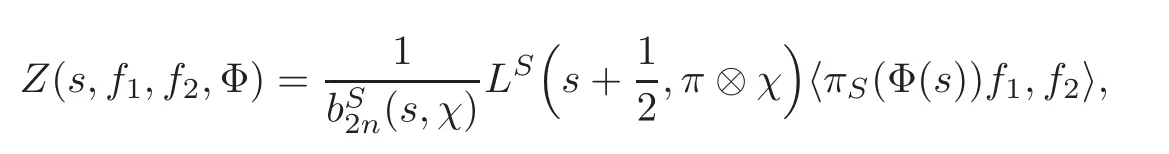
where ΦS(s)=

Assume thatf1andf2are factorizable vectors.Define local zeta integrals by

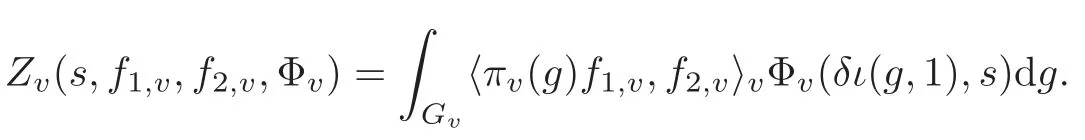
To be able to have a result about poles ofL-functions,we need to control local zeta integrals.As in the case of orthogonal-symplectic groups(see[7]),by choosing Φ whose support is sufficiently small,we have the following lemma for quaternion groups.

Lemma 4.1(see[7,12]) (1)Assume that v is non-archimedean.For anythere exists a choice ofsuch that

for all s∈C.In particular,

for such a choice.

(2)Assume that v is archimedean.For any s0∈C,there exist andΦvsuch that the local zeta integral is nonzero at s0.

Corollary 4.1Suppose that f1,f2∈π are Kvinvariant for v∈S.Assume that for each v∈S,,andΦvsatisfy the conditions of Lemma4.1.Then

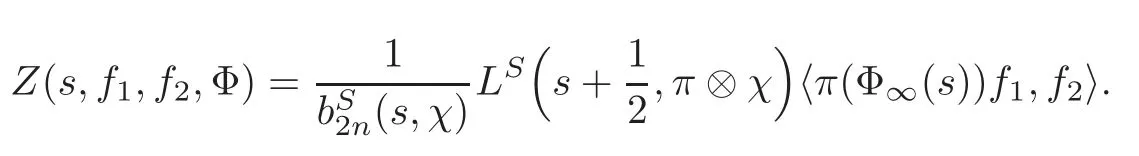
From here we have

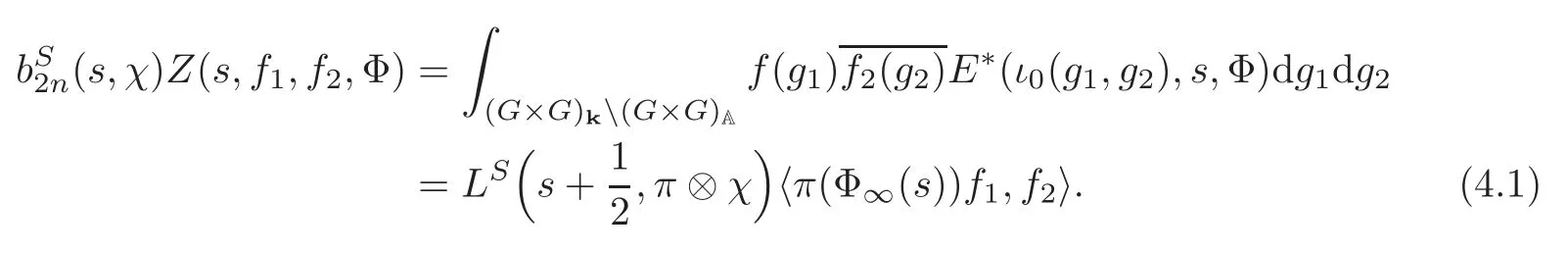
Therefore,any pole ofmust be a pole ofE∗(g,s,Φ)for a suitable choice of Φ and we have the following corollary.

Corollary 4.2(1)(s,π⊗χ)is entire.

(2)If=1,thenhas at most simple poles and these can only occur for

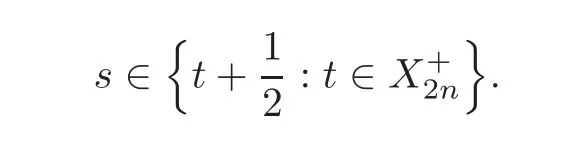
From now on assume thatχ2=1.and assume thatFixf1andf2and choose Φ(s)as in Corollary 4.1.From(4.1),we have

The regularized SWKR-formula and theta correspondence allow us to improve the result in Corollary 4.2.Forthe theta lifting offis defined by

Then ΘV(π)={θ(f,Φ)|f∈π,Φ∈is an invariant subspace of the space of automorphic forms onH(A).Following Proposition 7.2.4 of[7],we have the next proposition.

Proposition 4.1ForletΦ =Then we have

where c is a nonzero constant,z0is the element in the Bernstein center of H used in the regularization of theta integrals.

Letrbe the dimension of a maximal totally isotropic subspace ofV.We may writeVas a sumV=whereis a split-Hermitian space of dimension of 2r.Let=−m.Then we have the following vanishing result in theta correspondence.

Lemma 4.2(see[7])=0if m0=dimV0＜n.

Now we can improve the result in the previous corollary by removing about half of the possible poles.

Theorem 4.1(Main Theorem)If χ2=1,then LS(s,π⊗χ)has at most simple poles and these can only occur for s∈:tand t−n=1,2,···,n+Heres=2is not included in the set when n=1,=1and χ=1.

ProofSuppose that there exists a pole ats∈Letand Φ(s)as in Corollary 4.1.Ifhas a pole(with a nonzero residue)ats=s0,then from(4.2)we conclude that the integral ofagainstf⊗is nonzero.By using the regularized SWKR formula,we see that there exists at least one quadratic spaceV0of dimensionm0,a character=χand a function Φ =such that the functionhas a nonzero integral againstf⊗f.By Proposition 4.1,we see that/0.This means thatFrom the previous lemma,this is possible only ifm0≥n.Therefore,we havenwhich implies

Remark 4.1In[13],Yamana gave a theorem in which the set of possible poles ofLS(s,π⊗χ)includes negative numbers.In the main theorem,we improve this result by removing possible poles in the left-half plane.

AcknowledgementsThe author would like to thank Professor Jianshu Li and the referees for their valuable suggestions and support.

[1]Arthur,J.,Eisenstein series and the trace formula,Automorphic Forms,Representations andL-Functions,Amer.Math.Soc.,Providence,R.I.,1979,253–274.

[2]Casselman,W.,The unramified principal series ofp-adic groups,I,the spherical function,Compositio Math.,40(3),1980,387–406.

[3]Garrett,P.B.,Pullbacks of Eisenstein Series;Applications,Automorphic Forms of Several Variables,46,Progr.Math.,Birkhuser Boston,Boston,MA,1984,114–137.

[4]Gelbart,S.,Piatetski-Shapiro,I.and Rallis,S.,Explicit Constructions of AutomorphicL-Functions,1254,Lecture Notes in Mathematics,Springer-Verlag,Berlin,1987.

[5]Howe,R.,θ-Series and Invariant Theory,Automorphic Forms,Amer.Math.Soc.,Providence,R.I.,1979,275–285.

[6]Kudla,S.S.and Rallis,S.,Poles of Eisenstein Series andL-Functions,Festschrift in Honor of I.I.Piatetski-Shapiro on the Occasion of His Sixtieth Birthday,Part II(Ramat Aviv,1989),3,Israel Math.Conf.Proc.,Weizmann,Jerusalem,1990,81–110.

[7]Kudla,S.S.and Rallis,S.,A regularized Siegel-Weil formula:the first term identity,Ann.of Math.,140(1),1994,1–80.

[8]Langlands,R.P.,On the Functional Equations Satisfied by Eisenstein Series,Lecture Notes in Mathematics,544,Springer-Verlag,Berlin,1976.

[9]rti¸s,C¸.,Special values ofL-functions by a Siegel-Weil-Kudla-Rallis formula,J.Number Theory,125(1),2007,149–181.

[10]rti¸s,C¸.,Poles of Eisenstein series on quaternion groups,J.Number Theory,130(9),2010,2065–2077.

[11]Weil,A.,Sur la formule de Siegel dans la thorie des groupes classiques,Acta Math.,113,1965,1–87.

[12]Yamana,S.,L-Functions and theta correspondence for classical groups,Inventiones Mathematicae,2013,DOI:10.1007/S00222-013-0476-x.

[13]Yamana,S.,On the Siegel-Weil formula for quaternionic unitary groups,Amer.J.Math.,135(5),2013,1383–1432.