Monomial Base for Little q-Schur Algebra uk(2,r)at Even Roots of Unity

Qunguang YANG

1 Introduction

The infinitesimal Schur algebras(n,r)hwas introduced in[7]to study the polynomial representation ofGhTof a given degreer,whereGhTis the group scheme associated to ther-th Frobenius kernelGhand a maximal torusTof the general linear group gln.The quantum version of the infinitesimal Schur algebra was studied by Cox in[2–3].Semisimple infinitesimal Schur algebras were classfied in[6]and semisimple infinitesimalq-Schur algebras were classfied in[17].The finite representation type of infinitesimal Schur algebra was classified in[8]and the tame representation type of infinitesimal Schur algebra was given in[4].The finite representation type of infinitesimalq-Schur algebra was given in[16]and the tame representation type of infinitesimalq-Schur algebra was given in[18].The structure of the endomorphism ring of tensor space as a module for the infinitesimalq-Schur algebrasq(2,r)1was investigated in[13].

Littleq-Schur algebrauk(n,r)was introduced in[11,15]and the construction of various bases of monomial,BLM and PBW types foruk(n,r)was given.Herekis a field containing anl′-th primitive rootεof 1.There is a close relation between infinitesimalq-Schur algebrasq(n,r)hand littleq-Schur algebrauk(n,r).In fact,littleq-Schur algebra can be considered as a subalgebra of infinitesimalq-Schur algebra(see[14]).The irreducible modules for littleq-Schur algebras and semisimple littleq-Schur algebras were classified in[12].The basic algebra of the endomorphism ring of tensor space as a module for the littleq-Schur algebrauk(2,r)was determined in[20].

In[11,Theorem 8.2,Theorem 8.5],various bases for littleq-Schur algebrauk(n,r)were obtained whenl′≥3 odd.And the case whenl′≥4 even was studied in[15].In[19,Theorem 5.1],the construction of aB-basis for littleq-Schur algebra(n,r)was given whereB=andεis anl′-th primitive root of 1 with3 being odd.In this paper,we shall construct a certain monomial base for littleq-Schur algebrauk(2,r)whenl′≥4 even.

We organize this paper as follows.In Section 2 we recall the definition of littleq-Schur algebras,given in[11,15].We shall construct a certain monomial base for littleq-Schur algebrauk(2,r)in Section 3.

Throughout,letυbe an indeterminate and letZ=Letkbe a field containing anl′-th primitive rootof 1 withl′≥3.Letl＞1 be defined by

Specializingυtoε,kwill be viewed as aZ-module.

2 The Little q-Schur Algebra

The quantized enveloping algebra of glnis the algebra U(n)=U(gln)over Q(v)generated by the elements

subject to the following relations:

Following[21–22],letUZ(n)be theZ-subalgebra of U(n)generated by allandwhere form,t∈N andc∈Z,

with[m]!=[1][2]···[m]and[i]=

For any integersc,twitht≥0,let

Ifc≥t≥0,we havewhile ift＞c≥0 we have=0.

Let(n)=(n)⊗Zk.We denote the images ofEi,Fi,KjinUk(n)by the same letters.Let(n)be thek-subalgebra ofUk(n)generated by the elementsfor alli,j.Let(n)be thek-subalgebra of(n)generated by the elements

We denote

Let UZ(n,r)be the algebra overZintroduced in[1,§1.2].It has a normalizedZ-basisdefined in[1].From[9],the algebra UZ(n,r)is isomorphic to theq-Schur algebraSq(n,r).Let U(n,r)=UZ(n,r)⊗ZQ(v),then we call both UZ(n,r)and U(n,r)asq-Schur algebras.

Givenr＞0,A∈Ξ±(n)and j=∈Zn,we define

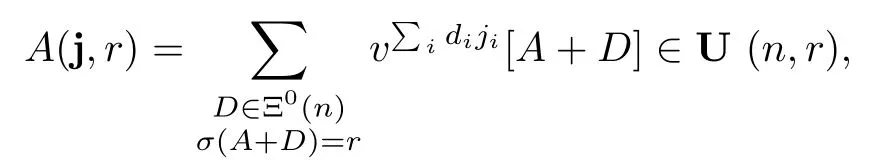
whereD=diag(d1,d2,···,dn).

Theorem 2.1(see[1])There exists an algebra epimorphism ζr:U(n)U(n,r)satisfying

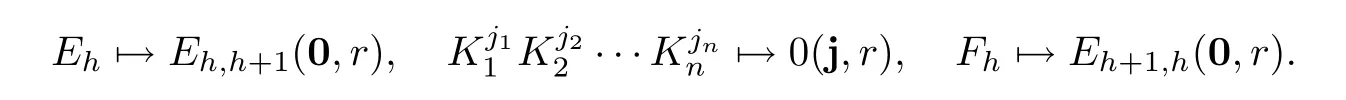
Denote ei=1≤i≤n−1,1≤j≤n.For t=

Define a map :Zn→For j=∈Nn,let kj=σ(j)=j1+···+jn,Nl′={0,1,···,l′−1}⊆Z.Let Λ(n,r):={λ∈Nn|σ(λ)=r}.

Denote(n,r)be the subalgebra generated by kλ(λ∈Λ(n,r))of UZ(n,r).

Theorem 2.2(see[5,10])(1)The set{|λ ∈Λ(n,r)}is a complete set of orthogonal primitive idempotents(hence a basis)for(n,r).In particular,1=

(2)Let λ∈Λ(n,r).Then

Let Uk(n,r)=(n,r)k.According to[9],we have=UZ(n,r).Thus,could naturally induce an epimorphismFor convenience,we denoterespectively.Then the algebrais called a littleq-Schur algebra(see[11,15]).Let

Denote

ForA=∈Ξ±(n),we define

ForA∈Γ±(n),∈we define

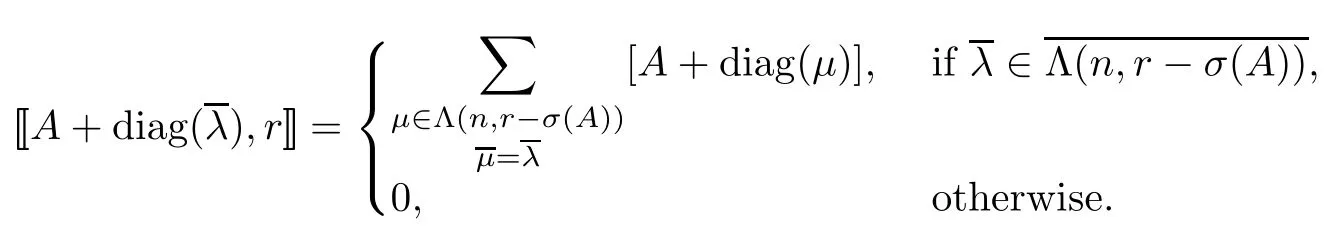
ForA=()∈(n)andi＜j,let(A)=DefineA′Aif and only ifandfor all 1≤i＜j≤n.PutA′AifA′Aand,for some pair(i,j)withi＜j,either(A)or(A).

ForA=()∈Ξ(n),we define

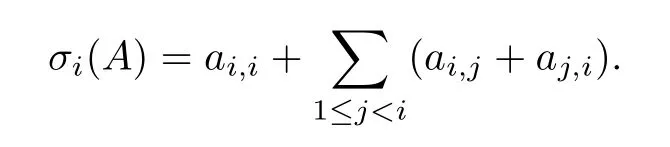
Lemma 2.1(see[11,Proposition 7.3],[15,Corollary 6.2])Each of the following sets forms a k-basis for the algebra(n,r):

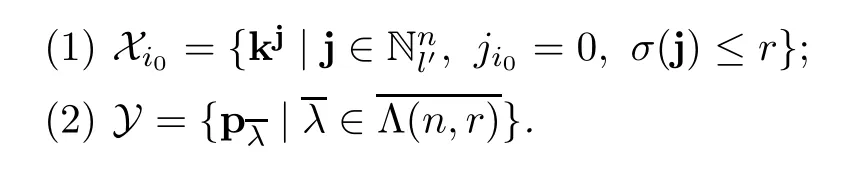
Lemma 2.2(see[11,Theorem 8.2,Theorem 8.5],[15,Theorem 6.8,Theorem 6.9])Each of the following sets forms a k-basis for the little q-Schur algebra uk(n,r):

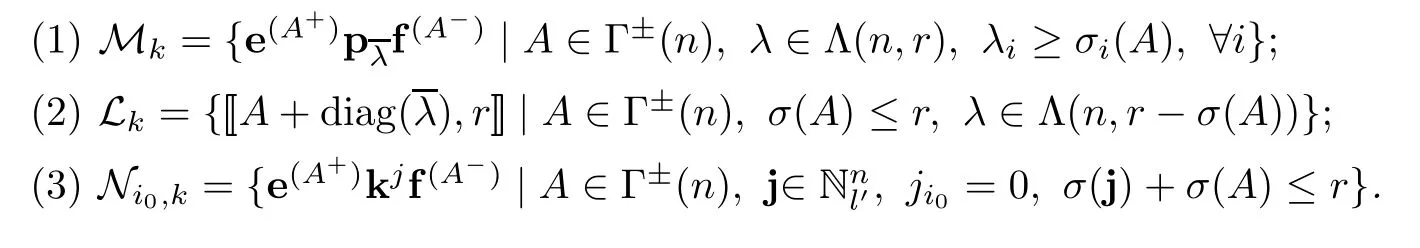
Assume thatl′is even.Let

It is conjectured by Qiang Fu that the setforms ak-basis foruk(n,r).We will prove that this conjecture is true whenn=2 andl′is even.

We have following results:

Lemma 2.3Assume that l′is even.There exists a bijection between the set

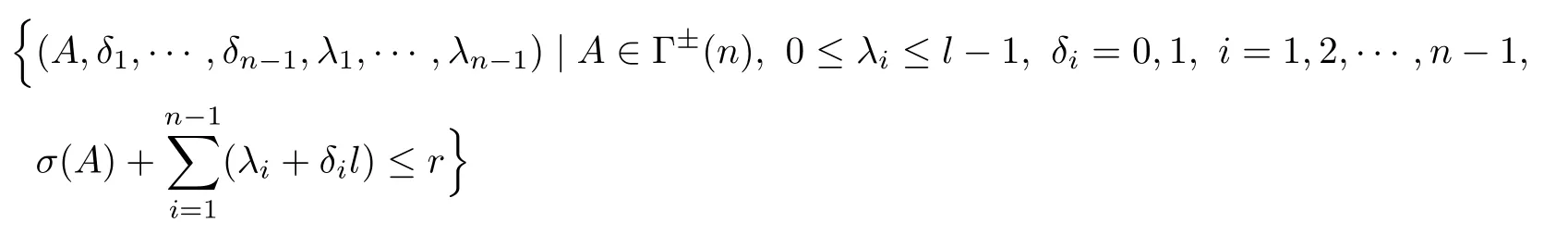
and the set

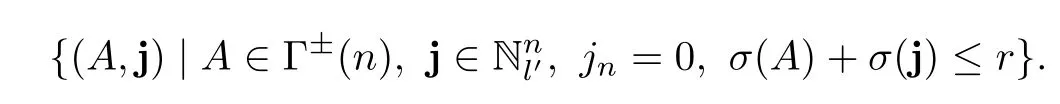
ProofWe establish a map between the two sets as

Then it is easy to know that the map is a bijection.

According to the lemma above,we can establish a bijection between the setand the setin Lemma 2.2(3).

Similarly,there exists a bijection between the following two sets.

Lemma 2.4Assume that l′is even.There exists a bijection between the set

and the set

Then we can establish a bijection between the setand the setin Lemma 2.1(1).

3 Monomial Base for uk(2,r)

Denote

Proposition 3.1Assume that l′is even.Then the set

forms a k-basis for(2,r).

ProofWe shall carry out the proof in three cases.

Case 1r＜l.

We fix an order inY=

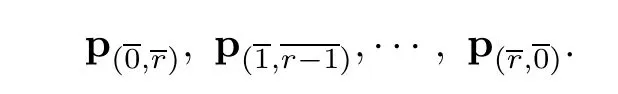
The elementsare

Hence,we will fix an order inas follows:

According to(2.1),each elementcan be written as ak-linear combination of(∈

Applying the above order,we know that the matrix between vectors consisting of elements inand vectors consisting of elements inYis a square matrix according to Lemma 2.4.We denote by this matrixBy Lemma 2.1(2),Yis ak-basis of(2,r),it is sufficient to show thatis invertible.

is the following matrix:

where the first column vector inBrcorresponds to the element 1 inthe second column vector inBrcorresponds to the elementinthe third column vector corresponds to the element···,the(r+1)-th column vector inBrcorresponds to the element

Apparently,Bris a lower triangle matrix with diagonal elements 1 and hence,it is invertible.

Case 2l≤r≤l′−1.

Letr=l+b,0≤b≤l−1.We have

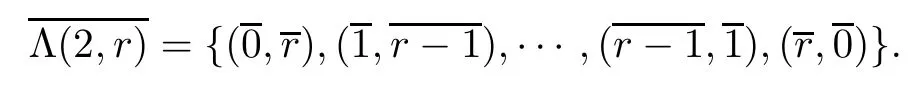
We also fix an order inY=

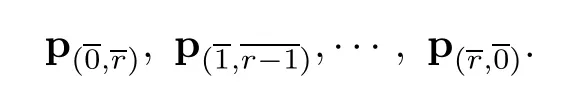
The elementsare

Therefore,we shall fix an order inas follows:

Similarly,each elementcan be also written as ak-linear combination of∈and we denote the matrix between vectors consisting of elements inand vectors consisting of elements inYbyBr.Now we will show thatBris invertible.

Bris the following matrix:

where the first column vector inBrcorresponds to the element 1 inthe second column vector inBrcorresponds to the element···,thel-th column vector correspondsto the elementinthe(l+1)-th column vector corresponds to the element k1inthe(l+2)-th column corresponds to the element···,the(l+b+1)-th column vector corresponds to the element

Observe the determinant,there exists only one non-zero element 1 inl-th column which is in thel-th row.There exist two non-zero elements 1 in the(l−1)-th column which are in the(l−1)-th row and thel-th row.Counting the number of non-zero elements in each column in turn,we know that there arel−b−1 non-zero elements 1,in the(b+2)-th column which are in the(b+2)-th,(b+3)-th,···,l-th row,respectively.

Therefore,we can simplify thel-th,(l−1)-th,···,(b+2)-th columns in turn.Then we have

Next we add−1 multiple of the first row vector to the(b+2)-th row vector and obtain|Br|

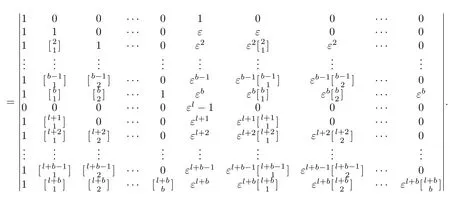
Note that the(b+2)-th row vector now has only one non-zero elementεl−1.So we simplify the(b+2)-th row in|Br|and we have

It is a determinant of order 2b+1.

Now,the first row vector has only one non-zero element 1.So we can simplify|Br|with respect to the first row and we have

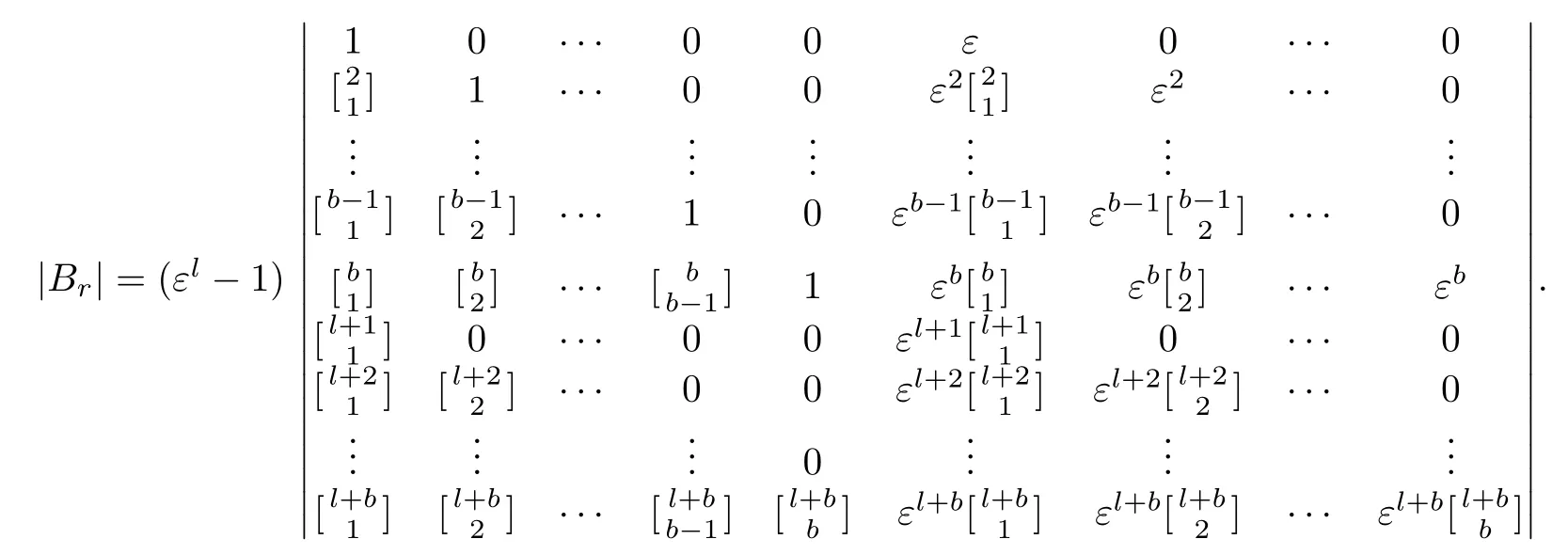
And it is a determinant of order 2b+1.

Continuing in this way we finally get that

In particular,in the case ofr=is the following matrix:

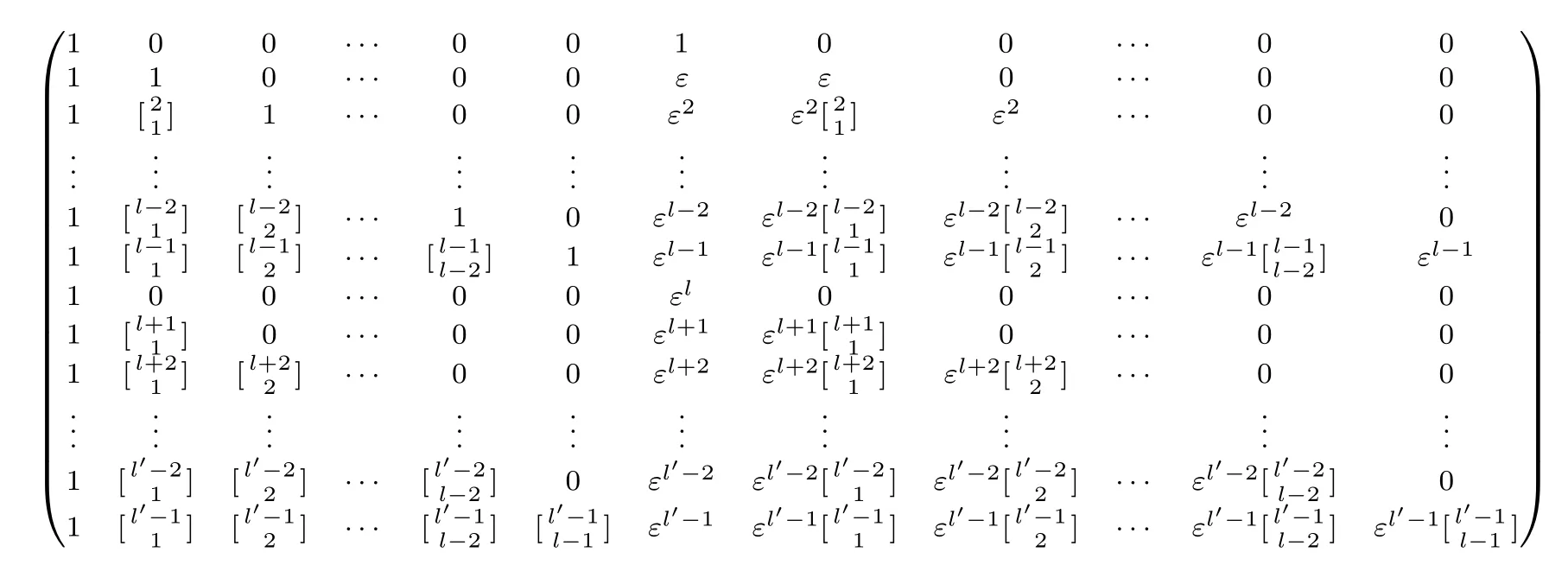
and

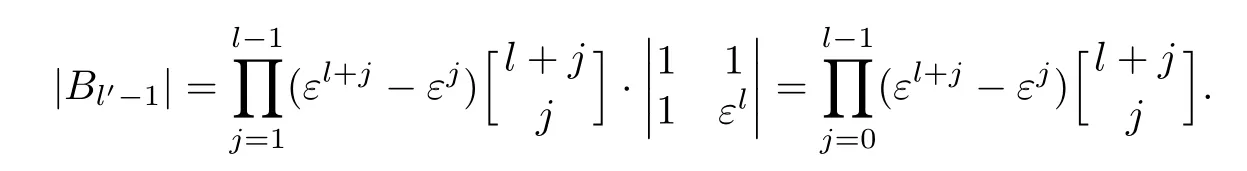
Apparently,Bris invertible.

Case 3r＞l′−1.

Letr=l′+b,b≥0.We have that

And we choose an order inY={|}as follows:

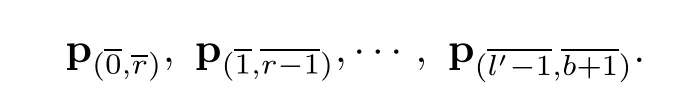
The elementsare

Similarly,we fix an order inas

and denote the matrix between vectors consisting of elements inand vectors consisting of elements inYbyBr.

Since in the caser≥l′−1 we haveit is easy to know that

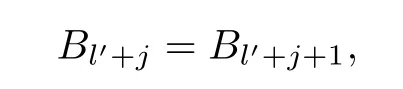
wherej≥−1.

Therefore,we have0 for anyr＞0,that is,Bris invertible.The assertion follows.

Now we give our main result in this paper which shows that the conjecture given above by Fu is true in the casen=2.

Theorem 3.1Assume that l′is even.Then the set

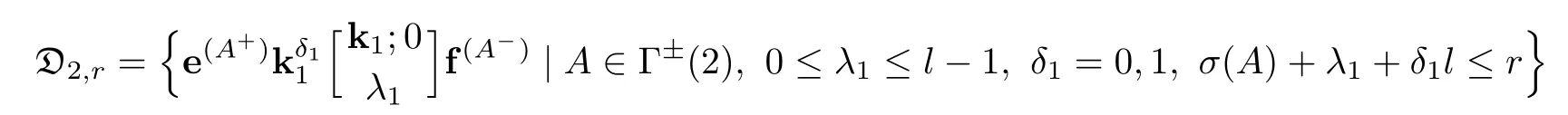
forms a k-basis for uk(2,r).

ProofObviously,σ1(A)=0 for anyA∈Γ±(2).By Theorem 2.2,we have

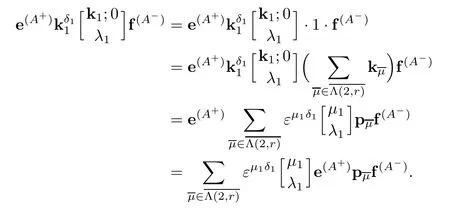
Then by[1],[19,Theorem 5.1(3)],[10,Theorem 5.5,Corollary 5.6]and Lemma 2.4,we obtain that

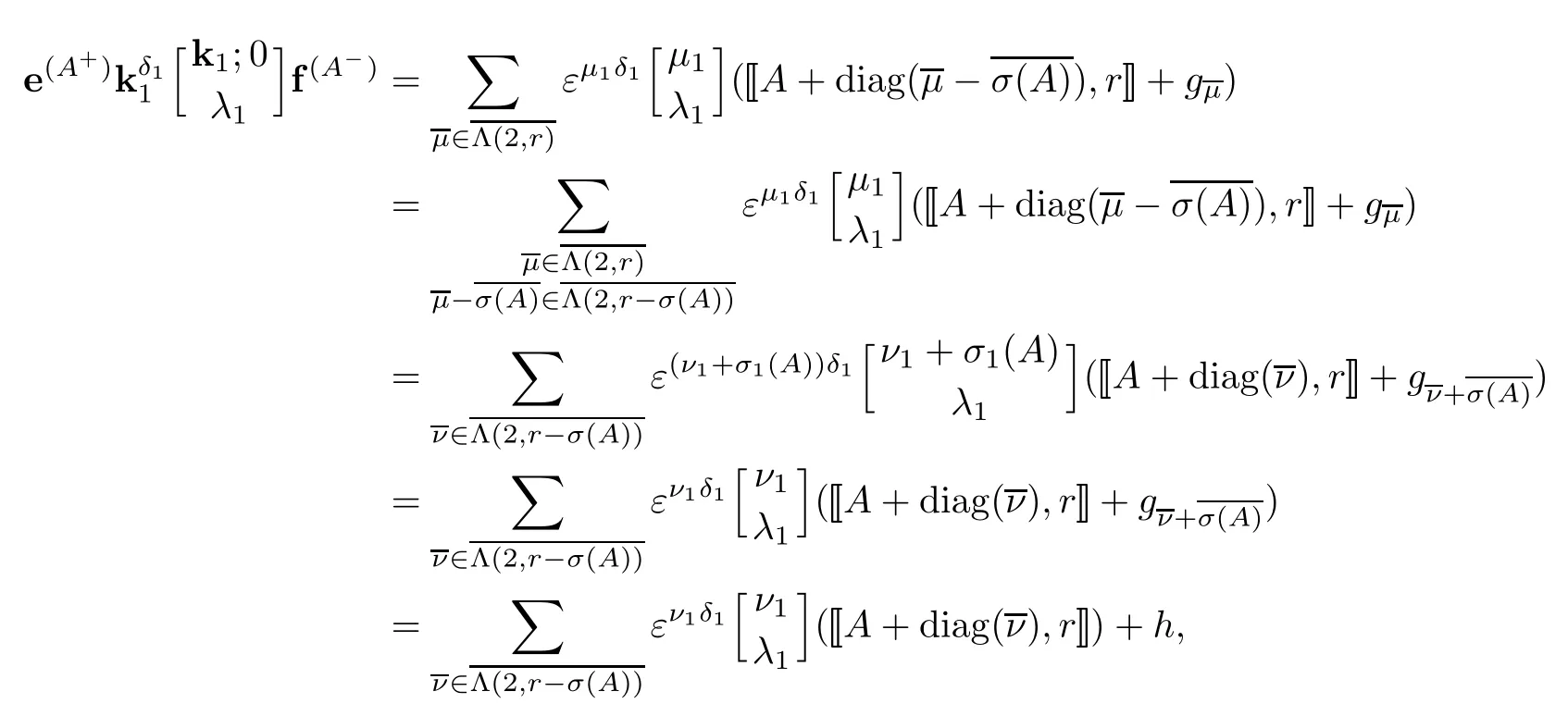
whereν=(A)forμ=ν,μ∈Λ(2,r).In particular,ForA∈Γ±(2),

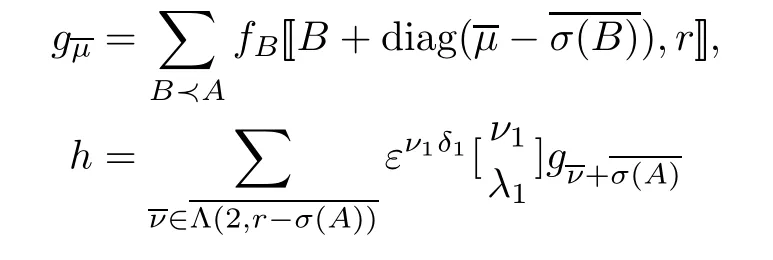
for somefB∈k.

It is easy to know that the matrixis invertible.Thus,the elements inarek-linearly independent.And the assertion holds.

[1]Beilinson,A.,Lusztig,G.and MacPherson,R.,A geometric setting for the quantum deformation ofGLn,Duke Math.J.,61,1990,655–677.

[2]Cox,A.,On some applications of infinitesimal methods to quantum groups and related algebras,University of London,1997.

[3]Cox,A.,On the blocks of the infinitesimal Schur algebras,Quart.J.Math.,51,2000,39–56.

[4]Doty,S.,Erdmann,K.,Martin,S.and Nakano,D.,Representation type of Schur algebras,Math.Z.,232,1999,137–182.

[5]Doty,S.and Giaquinto,A.,Presenting Schur algebras,International Mathematics Research Notices,36,2002,1907–1944.

[6]Doty,S.and Nakano,D.,Semisimple Schur algebras,Math.Proc.Cambridge Philos.Soc.,124,1998,15–20.

[7]Doty,S.,Nakano,D.and Peters,K.,On Infinitesimal Schur algebras,Proc.London Math.Soc.,72,1996,588–612.

[8]Doty,S.,Nakano,D.and Peters,K.,Infinitesimal Schur algebras of finite representation type,Quart.J.Math.,48,1997,323–345.

[9]Du,J.,A note on the quantized Weyl reciprocity at roots of unity,Alg.Colloq.,2,1995,363–372.

[10]Du,J.and Parshall,B.,Monomial bases forq-Schur algebras,Trans.Amer.Math.Soc.,355(4),2003,1593–1620.

[11]Du,J.,Fu,Q.and Wang,J.P.,Infinitesimal quantum glnand littleq-Schur algebras,J.Algebra,287,2005,199–233.

[12]Du,J.,Fu,Q.and Wang,J.P.,Representations of littleq-Schur algebras,Pacific J.Math.,257(2),2012,343–378.

[13]Erdmann,K.and Fu,Q.,Schur-Weyl duality for infinitesimalq-Schur algebrassq(2,r)1,J.Algebra,320,2008,1099–1114.

[14]Fu,Q.,A comparison of infinitesimal and littleq-Schur algebras,Comm.Algebra,33,2005,2663–2682.

[15]Fu,Q.,Littleq-Schur algebras at even roots of unity,J.Algebra,311,2007,202–215.

[16]Fu,Q.,Finite representation type of infinitesimalq-Schur algebras,Pacific J.Math.,237(1),2008,57–76.

[17]Fu,Q.,Semisimple infinitesimalq-Schur algebras,Arch.Math.,90,2008,295–303.

[18]Fu,Q.,Tame representation type of infinitesimalq-Schur algebras,J.Algebra,320,2008,369–386.

[19]Fu,Q.,On Schur algebras and little Schur algebrass,J.Algebra,322,2009,1637–1652.

[20]Fu,Q.and Yang,Q.G.,On the structure ofJ.Math.Phys.,52,2011,083507,10 pages.

[21]Lusztig,G.,Finite dimensional Hopf algebras arising from quantized universal enveloping algebras,J.Amer.Math.Soc.,3,1990,257–296.

[22]Lusztig,G.,Canonical bases arising from quantized enveloping algebras,J.Amer.Math.Soc.,3,1990,447–498.