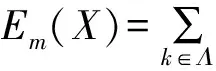保险产品设计的数学模型
高婷婷, 张明会
(陇南师范高等专科学校初等教育学院, 甘肃成县 742500)
保险产品设计的数学模型
高婷婷, 张明会
(陇南师范高等专科学校初等教育学院, 甘肃成县 742500)
在已知投保人恰好k岁死亡的概率为pk的前提下,以保险金本息和余额为随机变量X,建立了保险公司收益的数学期望Em(X)=∑k∈Λxkpk的概率模型.并给出了在投保人都是恰好满m岁死亡时,保险公司收益的数学期望的表达式,讨论了保险公司不盈不亏(即保险公司收益的数学期望Em(X)=0时)的概率p(Em(X)=0).通过考虑年龄别死亡率等一些有用的数据,讨论了确定合适的a,b,d和n值的一些思路和方法.
概率模型;概率分布列;数学期望;均匀分布
1 问题的提出和复述
某保险公司拟设计一款新产品, 其思路是:投保人从一出生开始, 每月交纳固定费用a元, 交满n年(n是正整数)后停止交费, 并从下一个月开始按月领取固定额度的工资b元, 直到投保人死亡.
为简单起见, 我们不需要考虑其他例外情况. 假设银行的月利率为c, 且一直不变. 保险公司只将投保人的交费及时存入银行, 不进行其他投资.
由于人的死亡具有一定的随机性, 若已知投保人恰好k岁死亡的概率为pk, 试建立合理的数学模型, 并解答如下的问题.

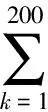
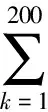
问题4: 从直觉上知道,a,n越小,b,d越大, 投保者越多. 但也可能使公司的风险增大. 根据以上模型, 探讨如何确定合适的a,b,d,n(可以引入以上没有提及的影响因素).
2 模型的假设与变量说明
为了简化模型, 便于讨论和计算, 现对模型中的变量和符号进行说明, 并做一些合理的假设.
2.1 必要的假设
1. 当投保人交满n年保险金后, 并在m年死去, 当m>n时投保人除了按月领取b元固定工资外, 保险公司不另行其他赔偿; 当m≤n时保险公司全额退还投保人所有交费(不付利息), 并再按所有交费的d倍赔付.
2. 月份按自然月计算, 每年12个月, 即不分大月和小月, 也不考虑闰年, 人在一年中的死亡率服从均匀分布.
3. 保险公司每月月初将投保人的保险金存入银行.
4. 银行的存款利息按复利计算, 即银行在每月月底结息, 并自动滚入下一月, 作为下一月的本金.
5. 投保人交满n年保险金后, 从第n+1年开始每月月初领取工资b元.
6. 投保人在m年死亡后, 其保险金本息和的余额作为保险公司的纯收益, 不再考虑利息.
2.2 变量和符号说明
a 表示投保人每月交纳的保险金(元);
b 表示投保人每月领取的工资(元);
n 表示投保人交纳保险金的年限(年);
m 表示投保人死亡的年限(年);
c 表示银行利率;
E(X)表示随机变量X的数学期望;
[x]表示数x的取整函数;
∑表示求和符号.
3 主要数据及公式的引用
第一阶段在考虑复利的情况下, 讨论了投保人保险金本息和的计算及领取工资后保险金本息和余额的计算, 现引述如下.
3.1 投保人n年共交纳的保险金及本息和[1]
由假设3和4, 投保人在交纳保险金的n年中各个月份(共12n个月)中, 所缴纳的保险金及本息和的计算, 可用表1表示.
为了以后计算和表示方便, 记
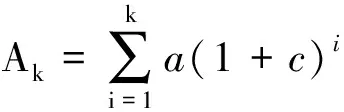
.
3.2 投保人开始领取工资后, 保险金余额
由假设4和5, 投保人在交纳完n年保险金后的下一月月初开始领取固定工资b元, 并在第m年(m>n)死去, 共12(m - n)个月, 则其所交纳的保险金本息和余额的计算, 可用表2表示.

表2 领取工资后保险金本息和余额表
为了方便讨论, 记
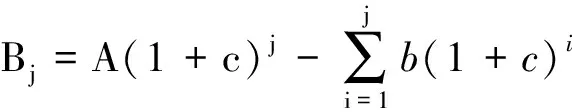
这里A=A12n.
3.3 数据的化简和计算
在以上的表示中,
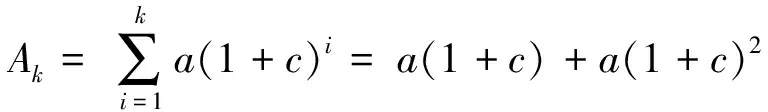
是以a1=a(1+c)为首项, 以q=(1+c)为公比的等比数列, 由等比数列的前n项和公式, 对上式求和就有
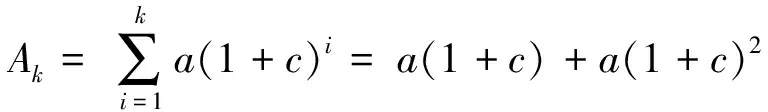
a(1+c)j+...+a(1+c)k
同理,
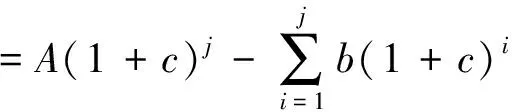
从以上可知,Bj为投保人领取工资到j个月时, 所交纳的保险金的余额在月底的本息和.
4 模型的建立及问题的解答
4.1 问题1的建模及解答
根据以上对表1和表2的讨论和计算, 现对文中提出的问题1, 建立模型并解答.
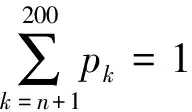

k/年n+1n+2n+3…n+k…200XB12B24B36…B12(k-n)…B200ppn+1pn+2pn+3pn+k…p200
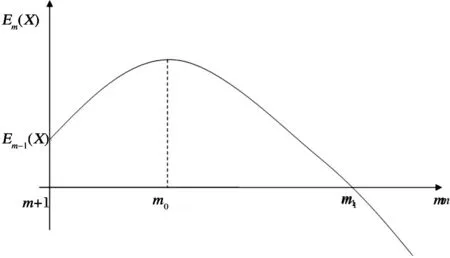
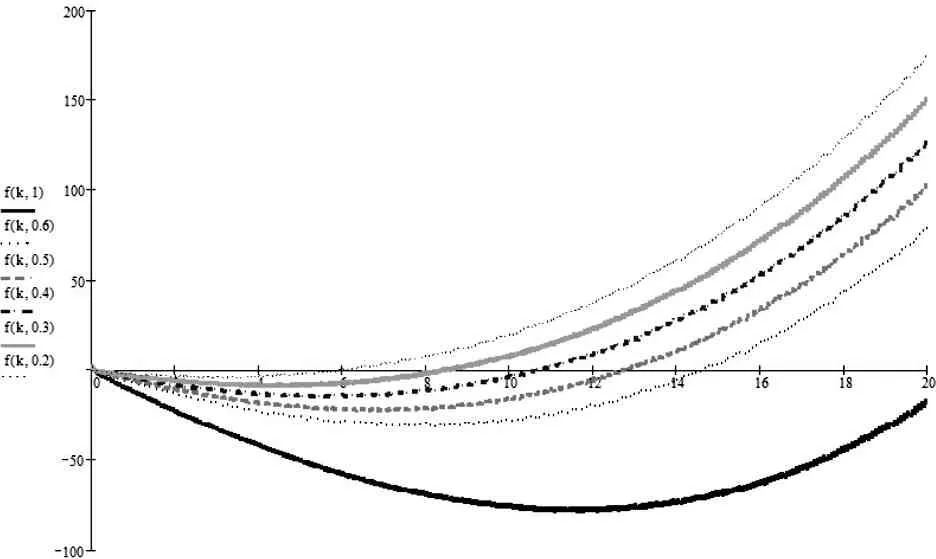
由于要保证保险公司不盈不亏, 就是说如果投保人保在第m1年(n (1+c)12(k-n))-b((1+c)12(k-n)-1)]pk=0 化简得 (1) 因此, 若(1)式成立, 则保险公司不亏不赢的概率与投保人恰好m1岁死亡的概率一致为p(Em1(X)=0)=pm1. 下证(1)式成立 由第一阶段的讨论知, 领取工资后保险金本息和余额Bj有如下的性质 因此, 必存在一点m1∈[n+1,200], 使得Em1(X)≥0而Em1+1(X)<0. (1) 若Em1(X)=0, 则m1就是所求的年限; (2) 若Em1(X)>0而Em1+1(X)<0, 这说明在m1年保险公司略有盈余, 而在第m1+1年, 保险公司略有亏损, 保守认为m1就是所求的年限. 这就是说, 使(1)成立的m1是存在的.m1称为盈亏平衡点. 4.2 问题2的建模及解答 图1 Em(X)与m的关系图 k/年123…k…nXx1x2x3…xk…xnpp1p2p3pk…pn 则当投保人保m 岁(m ≤ n, m 为整数)死亡时, 保险公司收益的数学期望为 由于要保证保险公司不盈不亏, 就是说在第m2(m2 整理得 化简得 (2) 因此, 若(2)式成立, 则保险公司不亏不赢的概率为p(Em2(X)=0)=pm2.(2)式成立的证明与(1)的证明相似, 不再赘述. 因此, 保险公司不亏不赢的概率与投保人恰好m2岁死亡的概率一致为p(Em2(X)=0)=pm2. 4.3 问题3的解答 1.k≤12n时, 当投保人在第k个月死亡(k≤12n,k为整数)时, 保险公司的余额为 于是以余额为随机变量X, 其概率分布为 k/月123…k…12nXx1x2x3…xk…x12np112p1112p1112p1112p1+k-112[]…112pn 从而当投保人保在m 个月(m ≤12 n, m 为整数)死亡时, 保险公司收益的数学期望为 2.k>12n时, 当投保人在第k个月死亡(k>12n,k为整数)时, 保险公司的余额为xk=B12(k-n), 于是以余额为随机变量X, 其概率分布为 k/月12n+112n+212n+3…12n+k…2400XB1B2B3…Bk…B2400-12np112pn+1112pn+1112pn+1112p1+k-112[]…112p200 从而当投保人保m个月(m> 12n, m为整数)死亡时, 保险公司收益的数学期望为 于是, 保险公司收益的数学期望 由于要保证保险公司不盈不亏, 就是说在第m3(或M3)个月末, 公司收益的数学期望为零, 于是就有Em3(X)=0(或EM3(X)=0), 也就是 (3) 4.4 问题4的解答 在a,b,c,d,n和m这些数据中,c和m是保险公司不能随便改变的, 而a,b,d和n是保险公司在制定新产品时主要考虑的因素. 从第一阶段和以上的讨论可以发现,a,n越小,b,d越大, 对投保者来说越有利, 投保者也就越多, 但也可能使公司的风险增大. 图2 余额xm、 d 和n 之间的关系图 就是说, a,b,c,d,n和m的值是相互制约的, 从投保人的角度来看, a值和n值越小越好, a值和n值过高, 虽然保险工资b值会相应提高, 但投保人在经济上的压力增大; d和m越大越好, 但保险公司的风险又会增大. 从保险公司的角度看, 当然希望a, n的值高一些, b, d的值低一些, 保险公司的风险就小一些, 但这对投保人又会不利. 因此, 确定a,b,c,d,n和m的值需要综合考虑. 1. m的确定. 世界卫生组织公布《2008年世界卫生组织报告》, 报告显示, 我国男性平均寿命70岁, 女性平均寿命74岁, 人均寿命72岁[3]. 对保险公司来说, 可以作为m的参考值; 3.a的确定. 要确定合理的a值, 需要考虑当地人们的人均收入、 人均可支配支出、 可支配指出占实际收入的比例、 人们的参保意识、 投保人的保险收益以及保险公司的收益等多种因素. 其中人均收入是需要参考的重要因素, 这些数据可以根据当地的情况, 通过调查、 问卷、 统计等数学方法或通过网络搜索取得. 统计显示, 2010年中国农村居民人均纯收入5919元, 比上年增长14.9%, 扣除价格因素实际增长10.9%; 中国城镇居民全年人均可支配收入19109元, 增长11.3%, 实际增长7.8%.[4] 5.d的确定. 余额xm、d和n之间的关系见图2. 从中可以看出,d的值不能大, 否则余额为负值, 若以n=20为例,d的值宜在0.3到0.5之间选择, 过大可能亏损, 过小投保人的利益得不到很好的保护. 6. 年龄别死亡率. 年龄别死亡率(也称生命表), 也就是在某年龄段死亡人数与该年龄段总人数的比例, 也是必须考虑的因素之一. 2005年联合国卫生组织公布了我国生命表[5](见表3). 表3 联合国卫生组织公布的我国2005年生命表 从表中可以看到, 年龄别死亡率呈U字形, 在1岁以前死亡率较高, 然后逐年降低, 到10岁达到最低点, 以后又逐年增加. 这一点在制定保险方案时应充分考虑. 最后, 在考虑了年龄别死亡率等一些有用的数据后, 讨论了确定合适的a, b,d和 n值的一些思路. 模型具有结构简单, 计算方便等优势. 有较好的推广和应用价值. 模型存在的不足之处: (1) 没有考虑利率的变化. 在模型中, 银行的利率c一直没有变化, 这是不够完善的. 事实上, 银行的利率经常是变化的, 如2011年我国对银行利率进行了4次调整. 在实际应用时, 应该考虑到利率的变化对其他变量的影响; (2) 没有考虑寿命的延长对模型的影响. 事实上, 人的寿命会随着生活条件的改善而延长; (3) 没有考虑物价的上涨和货币贬值对保险业务的影响; (4) 在模型中假设了人的死亡率服从均匀分布, 这是不够合理的. 事实上, 老年人在11月到2月份, 由于气候等因素的影响, 死亡率比较高, 而在其他月份相对较低. 以上这些情况都对模型有一定的影响, 在处理实际问题时都应予以考虑. [1] 孔丽娜, 王芳君, 白博博. 保险产品的设计方案[Z].第四届数学中国数学建模网络挑战赛, 2011.4.22. [2] 袁长迎,等.掌握和精通Mathcad2000[M].北京: 机械工业出版社,2011. [3] 百度知道.人的寿命[EB/OL]. (2011-04-22).http://zhidao.baidu.com/question/77238412.html. [4] 天津网. 2010年中国城镇居民全年人均可支配收入19109元[EB/OL]. (2011-05-22).http://www.tianjinwe.com/hotnews/txjj/201102/t20110204_3354975.html. [5] 新浪网.资料分类.联合国卫生组织公布的我国2005年生命表[EB/OL].(2011-05-21).http://ishare.iask.sina.com.cn/f/4943272.html. [6] 周义仓, 赫孝良.数学建模实验[M].西安:西安交通大学出版社,2005.12. [7] 姜启源, 谢金星, 叶俊.数学建模[M].北京:高等教育出版社,2005.12. [责任编辑 胡廷锋] Mathematical Modal of Insurance Product Design GAO Ting-ting, ZHANG Ming-hui (College of Primary Education, Longnan Teachers College, Cheng County 742500, China) On the premise that the probabilitypkof that the insured dies atkyears of age, when X is the random variable of the premium principal, interest and balance, the probability model of the expectation of insurer’s revenue is established. The formula of the insurer’s revenue when the insured happen to die atmyears of age is established as follows: Whenm>n, Whenm≤n, On the assumption of uniform distribution, the formula of the insurer’s expected revenue when the insured happen to die atmyears of age is: On the basis of the above formulae, the probability of expected break-even point of the insurer is discussed. probability model; probability distribution series; mathematical expectation; uniform distribution 2017-02-27 陇南师范高等专科学校科研项目; 陇南师范高等专科学校教学改革项目; 陇南师专教改项目《数学建模教学方法改革与学生赛前训练》检验成果 高婷婷(1979—), 女, 甘肃礼县人, 讲师. 研究方向:基础数学. F840.48 A 1009-4970(2017)08-0063-07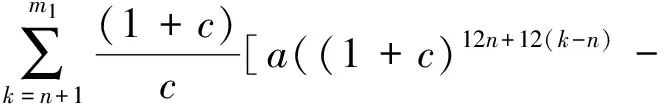
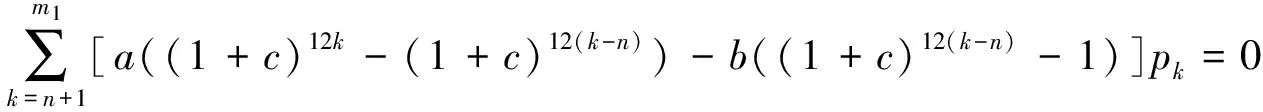
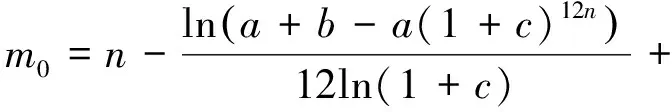

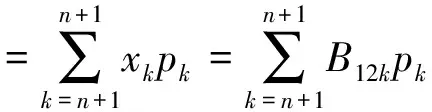
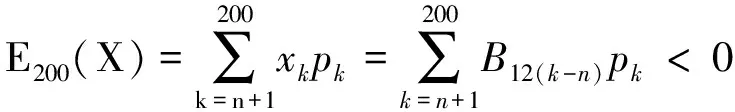
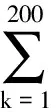

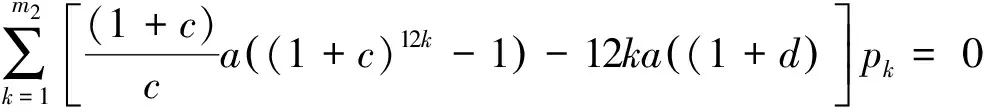
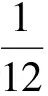
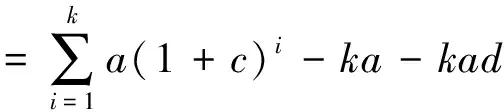


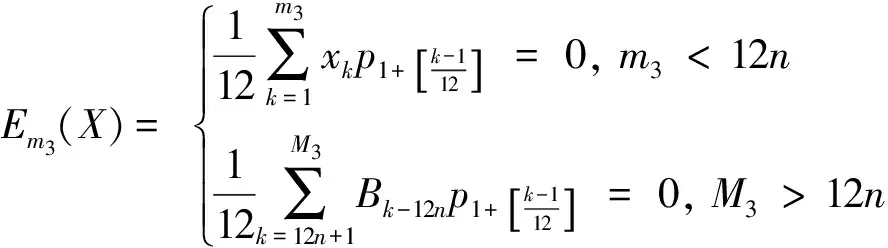
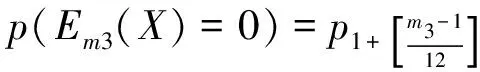
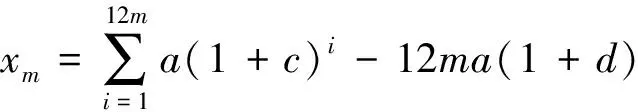
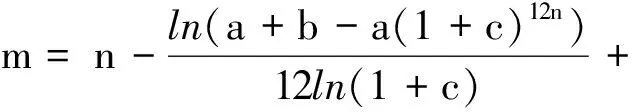
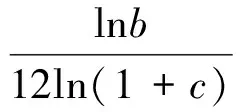
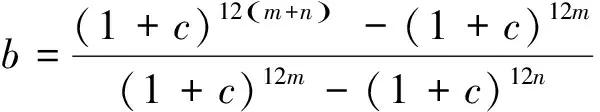

5 模型的评价与改进