玻尔兹曼统计力学的结构及其所包含的物理思想和方法
姜小兰
(新乡广播电视大学,河南 新乡 453000)
玻尔兹曼统计力学的结构及其所包含的物理思想和方法
姜小兰
(新乡广播电视大学,河南 新乡 453000)
本文以玻尔兹曼统计力学为例,探讨了如何构筑一个物理理念的结构,如何发掘一个物理理论的物理思想和方法等问题。在教材教法研究中,本文不仅是对玻尔兹曼统计力学的一个初步探讨,还可以作为学习和研究玻尔兹曼统计力学的参考资料。
结构;微观态;宏观态;平衡态;统计平衡态
众所周知,学习一个理论,如果不去把握它的整体,而停留于单个地掌握它的概念、定律等,其结果必定是事倍功半。实际上,人类早已认识到,掌握一个理论,应着力于掌握它的结构,因为从一个理论结构中,最便于提取知识、信息和方法。瑞士心理学家皮亚杰,更对结构理论作了深入的研究。他在《结构主义》一书中指出:“在人类科学的发展中,结构主义已经革新了,并将继续启发人类科学的理论形态。”“现代物理学对结构观点作出了愈来愈高的评价。”
所谓结构,简单地说,即是指若干成分以一定的关系组成的体系(或说整体)。一个物理理论,从问题的提出,理论体系的建立到运用和发展,包括了实验事实、假设、定律、思维过程和方法等若干成分,这些成分以一定的方式组成的和谐整体,便是这个物理理论的结构。一个物理理论的结构,不完全等同于该理论在形成和发展的历史过程中,某个科学家的实际思考过程,而是该理论各个成分更为和谐完美的组合,使之有更明显的逻辑线索,更便于提取物理知识、物理思想和方法。一个物理理论,由于成分的选择和组合的方式不同,构筑成的结构也是不相同的。这正好比差不多相同的建筑材料,既可能组合成华丽适用的大厦,也能组合成毫无用途的陋室。人们常说,“组合就是创造”,“所谓创造力,从某种意义上讲,就是调动知识单元重新组合的能力”。所以,恰当地选择一个理论的成分,并巧妙地组合成一个和谐、优美的理论结构,就是一个大的创造。
如何构成一个和谐优美的理论结构?如何更深刻地发展和发掘物理思想和方法,这些都尚属教材教法研究领域中有待于进一步探讨的问题。本文仅以玻尔兹曼力学为例,对这方面的问题作初步的探索。
本文拟将玻尔兹曼统计力学的主要成分划分为几个步骤,由这些步骤构筑成为一个层次明显的理论结构。在每一个步骤下,将简洁地叙述和分析该步骤所蕴藏的物理思想。
所谓物理思想,按人们通常理解的含义,是指获得物理概念、假设、定律等的思考过程。本文所叙述和分析的物理思想,有些是玻尔兹曼本人的思考过程,有些则是后人在分析理论体系的过程中补充的。把所有这些思考过程融合在一起分析,其目的是让理论结构浇铸在完整的思考体系中,并能充分地揭示理论结构和其包含的物理方法。
所谓物理方法,通常是指获得物理概念、假设、定律等的思维方法和操作方法。因为本文在每一步骤下所叙述和分析的物理思想,大部分属于物理方法方面的内容,物理方法已经较为明显地体现在物理思想的叙述和分析中,故以下论述没有专门列出标题归纳物理方法。
组成玻尔兹曼统计力学结构的几个步骤及其所包含的物理思想和方法
第一步 选择孤立系作为研究对象
建立物理理论的第一步,总是选择确定某种物理模型作为自己的研究对象。力学、电磁学、量子力学等,都无一不是首先选择和确定以什么的物理模型作为自己的研究对象。
玻尔兹曼试图建立热力学微观理论时,选择了孤立系作为自己的研究对象。由定义可知,孤立系是与外界既无质量交换也无能量交换的系统。绝对的孤立系是不可能实现的,只是一个理想的物理模型。实际上,如果一个系统与外界进行的质量和能量交换,与它自身的质量和能量大小比较非常小,以致可以忽略不计时,便可以作为孤立系来处理,所以,一切处于热力学平衡态的系统都可以视为孤立系。玻尔兹曼之所以选择孤立系作为研究对象,是希望使理论的建立过程简化一些。但是,建立在孤立系基础上的统计力学理论不能研究涨落现象。
无数经验表明,在理解和运用理论方面出现的错误中,相当大一部分是忘了理论的研究对象。所以,在学习和运用理论的全过程中,必须自始至终明确研究对象。
第二步 选择描述系统状态的方法,提出函数关系式W=W(N、V、E)
纵观物理学各科的内容,也可以说,物理学就是研究物质系统的的状态变化规律的科学。所以确定研究对象后,建立物理理论的第二步,便应是选择系统状态的描述方法,这往往是既困难又关键的一步,这一事实,理工科表现得尤为鲜明。
玻尔兹曼怎么选择状态的描述方法呢?鉴于统计力学的目的是,从宏观物质系统的微观结构以及微观世界的动力学原理出发,并与概率论结合,进行逻辑推理,导出平衡系统的宏观性质和规律,所以统计力学确定状态描述方法时,必须分别确立宏观状态和微观状态的描述方法。分析统计力学的上述目的,玻尔兹曼自然会想到,借用热力学描述状态的方法描述宏观状态;借用经典力学描述状态的方法描述微观状态。当然,要具体实现对宏观状态和微观状态的描述,还有不少“细节”有待解决。
首先考察,如何具体地描述一个孤立系的宏观状态。对于一个不考虑其电磁性质的孤立系 (本文仅限于研究这种系统),与外界不交换能量,意味着体积V和能量E保持恒定;与外界不交换质量,则意味着粒子数N保持恒定,也可以反过来说,三个参量(N、V、E)都保持恒定的系统,必定是一个孤立系;(N、V、E)三个参量完全确定了一个孤立系。但是,还不能说(N、V、E)三个参量具体地描述了一个孤立系的宏观状态,因为参量(N、V、E)一定的孤立系,一般说,包括了从非平衡态、准平衡态到平衡态的一系列宏观状态。只有当孤立系已经处于热力学平衡态后,参量(N、V、E)才能完全描述了它的宏观状态。在统计力学中,当我们选用(N、V、E)三个参量中描述一个孤立系的宏观状态时,正是针对处于热力学平衡态的孤立系而言的。
如何具体实现对微观状态的描述呢?如果借用经典力学的方法,N个粒子的微观状态,可以用N个粒子的全部广义坐标和全部广义动量描述。在统计力学中,这种描述方法被形象地转换为相空间描述方法。统计力学中所用的相空间,通常分为μ空间和Γ空间两种。
μ空间是描述单个粒子力学状态的全部广义坐标和广义动量构成的多维空间。μ空间的一点对应了一个粒子的力学状态,N个点便对应了N个相同粒子的力学状态。所以,N个同种粒子组成的系统的微观状态,可以形象地用空间中的N个相点描述(相空间中的点称为相点)。但是,μ空间仅适于研究由同种粒子组成的理想气体系统,为了便于研究一般的系统,玻尔兹曼又引入了Γ空间。
Γ空间是由描述整个系统(N个粒子)的力学状态的全部广义坐标的广义动量构成的多维空间。Γ空间中的一点对应了N个粒子的力学状态,即对应了N粒子系统的一个微观状态,于是,任意系统的微观状态可形象地通过它的Γ空间的一个相点描述。
以上选用了(N、V、E)三个参量确定一个孤立系统,并描述它的热力学平衡态;选用了相空间中的相点描述系统的微观状态。至此,我们还不能够说状态描述的问题已经最后解决。因为选用这些方法描述状态还带有试探性,我们还不知道这些方法是否有利于理论体系的建立,是否能经受实践的检验。事实上,玻尔兹曼也是在改造了以上两种状态的描述方法后,才建立起玻尔兹曼统计力学的。他改造这两种状态的描述方法的方案,是通过以下创造性的分析提出来的。
统计力学的目的,也可以说是通过系统的微观性质获得其宏观性质和规律。为达此目的,首先得寻求一个连结微观状态和宏观状态的“桥梁”,显然作为连结微观和宏观“桥梁”的关系式,既不可能单纯依靠某个微观理论导出,也不可能单纯依靠某个宏观理论导出,因为它横跨了微观与宏观两个世界。对此,玻尔兹曼以非凡的直觉,深刻地意识到,一定的孤立(N、V、E)应该包含有确定的微观状态数W,即W同参量 (N、V、E)之间存在着一定的函数关系W=W(N、V、E)。如果说这一认识是正确的,函数关系W=W(N、V、E)便可能成为一个连结微观和宏观的桥梁关系式。随着玻尔兹曼统计理论的完成,人们无比惊奇地发现,函数关系式W=W(N、V、E)具有出乎意料的巨大功能:只要求得一个系统的W=W(N、V、E)的具体函数关系式,便可能导出该系统的全部热运动性质和规律。后面将具体讨论这方面的内容。
但是,函数关系式W=W(N、V、E)存在的本身同微观状态的经典力学描述方法相抵触,因为函数关系式W=W(N、V、E)存在的本身要求微观状态数W必须是有限的;而根据经典力学关于广义坐标和广义动量连续变化的观点,一定宏观状态包含的微观状态数必定是无穷大。如何克服这一障碍呢?可供选择的道路只有三条:
(1)放弃函数关系W=W(N、V、E)。
(2)放弃微观状态的经典描述方法。
(3)改造微观状态的描述方法,在保留用相空间描述微观状态的前提下,使微观状态数W=W(N、V、E)成为有限值。
玻尔兹曼相信函数关系W=W(N、V、E)应该是成立的,同时又没有理由否定微观粒子遵从经典力学这一当时的基本信念,于是,他选择了第三条道路。他认为统计力学要处理1019个以上的粒子的运动特性同热力学量之间的数量关系,1019个以上的经典力学方程必定含有大量对我们得到热力学量多余的信息。为了清除这些多余的信息,玻尔兹曼首先改造了基于经典力学基础上的μ空间。把μ空间划分为很多微小的相体积元,并规定:N个同种粒子组成的理想气体系统,在μ空间的N个相点的相体积元中的一种分布方式对应了一种宏观状态。N个相点在各个相体积元中的任意某种分布,可以描述如下:
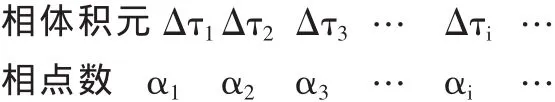
一般将注意第i个相体积元△τi中分布αi个粒子这样一种分布,简洁地表示为{αi}。分布{αi}中任意一个相体积元内中的相点数发生改变,都称为不同的分布,都对应了不同的宏观状态。在一定的分布{αi}下,任意两个相体积元内的相点交换便是不同的微观态。这样规定微观态的宏观态的描述方法后,一定宏观状态的微观状态数不仅是有限的,而且可以通过数学中的排列组合公式进行计算:分布{αi}对应的宏观状态所包含的微观状态数为
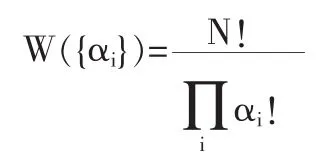
于是,由N个同种粒子组成的理想气体孤立系的总的微观状态数,为所有可能的微观状态数之和,即
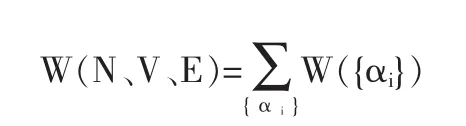
以后,人们又用类似的方法改造了Γ空间。对孤立系(N、V、E)的Γ空间将其等能面划分为很多微小的相体积元,把Γ空间中的一个相点对应于系统的一个微观态,改造为一个相体积元对应于一个微观态。这样,因等能面上的相体积数是有限的,孤立系的微观状态数便是有限的了。如果能够确定相体积元的具体大小,则可以通过计算等能面上的相体积元数求得孤立系的微观状态数W。待量子力学建立后,人们才得以确定相体积元△τ=hNr,其中h为普朗克常数,N为系统的粒子数,r为单个粒子的自由度数。以后,当我们说一个系统具有微观状态数W=W(N、V、E)时,就是对以上微观状态的描述方法而言的。否则,谈论系统的微观状态是没有意义的。
以上所述为玻尔兹曼统计力学结构的第二步——确定系统状态的描述方法。在这一步骤下的物理思想,着重阐述了玻尔兹曼宏观状态和微观状态的思考过程。玻尔兹曼的这些深刻而巧妙的思想,充分体现了他的远见卓识和开创精神。
第三步 给出统计平均态的定义,提出等先验几率假设
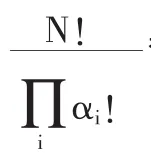
玻尔兹曼究竟是怎样定义统计平衡态的呢?实际上,玻尔兹曼提出了两种定义统计平衡态的方法:(1)一个孤立系的统计平衡态是它的最可几态;(2)一个系统的统计平衡态,是该系统长时间经历的微观态的平均值。
玻尔兹曼本人在第一种定义的基础上建立了玻尔兹曼统计力学;以后,吉布斯在第二种定义基础上建立了更加完美的吉布斯统计力学。这两种统计力学之所以有很大差别,可以说其根源就在于它们建基于不同的统计平衡态。本文仅限于讨论玻尔兹曼统计力学,以下不再涉及统计平衡态的第二种定义,以后的内容中所论及的统计平衡态都是就第一种定义而言的。

按第一种含义定义统计平衡态的思考,是从玻尔兹曼确定宏观态和微观态的描述方法开始的。当时他提出,组成孤立系的N个粒子的力学状态在μ空间各相体积元的一种分布{αi},对应了一种宏观态,一般说,一个孤立系可以处于微观状态。包括热力学平衡态和各种非平衡态。于是可以认为,N个粒子的N个相点在μ空间各相体元内的不同分布{αi},对应了不同的非平衡态。同时一定存在某个特殊分布{αi}最接近于热力学平衡态。可以想象,在“长时间观测”一个孤立系的过程中,这一特殊分布的出现次数应该远大于其他分布,出现时间应该远长于其他分布,当时玻尔兹曼已经知道运用等先验几率假设;“处于热力学平衡态下的孤立系统,各个可能在微观状态出现的几率是相等的”。根据等先验的几率假设,这样一特殊的分布是使微观状态数W({αi})最大的那一个分布,即最可几分布。既然最可几分布最接近于热力学平衡态,自然就可将它定义为统计平衡态,并可严格地表述为:“一个孤立系的统计平衡态,是它的最可几分布所对应的状态。”这便是第一种含义之下的统计平衡态的基础上形成玻尔兹曼统计理论的。
朗道和粟弗席兹著的《统计物理学》的前言中指出:“在玻尔兹曼的统计方法中,说明等先验几率假设的作用是很困难的。”笔者认为,在玻尔兹曼统计力学中,等先验几率假设是定义统计平衡态的理论基础,由于统计平衡态的定义,在玻尔兹曼统计力学中起着核心作用,等先验几率假设,作为它的理论基础的作用便不可等闲视之了。
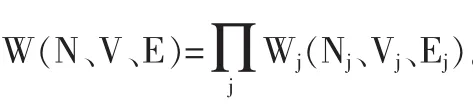
比较以上两种含义下的统计平衡态,可以看到,由于“最可几态”概念存在两种含义,或者说两种解释,玻尔兹曼提出的统计平衡态的第一种定义,“一定孤立系统计平衡态是它的最可几态”,实际上包含了两种颇为不同的统计平衡态。
以上所述为玻尔兹曼统计力学理论结构的第三步。在这一步骤下的物理思想,主要有:为什么需要定义统计平衡态;怎样定义一个统计平衡态;定义“孤立系的统计平衡态是它的最可几态”,实际上包含了两种颇为不同的统计平衡态。
第四步 建立统计平衡系统遵从的方程
统计平衡系统遵从的方程,自然应从统计平衡态的定义出发去寻求。如前所述,玻尔兹曼统计力学所采用的统计平衡态的定义,实际上包含着两种不同的统计平衡态,以下便分别从这两种含义不同的统计平衡态出发,建立起两套方程:
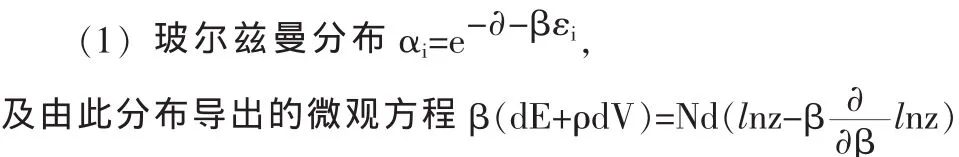
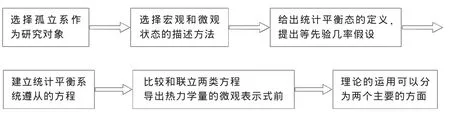
玻尔兹曼统计力学的结构简图
(2)l nW方程(因篇幅有限,建立这两套方程的具体过程从略了)
第五步 比较和联立两类方程,以导出热力学量的微观表示式
第四步导出统计平衡系统遵从的方程后,第五步的任务便是将统计平衡系统同热力学系统联系起来。联系的方法是,认为两类平衡态所反映的对象是一致的,因而它各自遵从的关系式是可以比较和联立的。分别将第四步建立的两套方程同热力学方程比较联立,我们可以看到,殊途同归,所得的热力学量的微观表示式是相同的(因篇幅所限,具体的比较和联立过程从略)。
在统计力学中,用比较和联立两类方程的方法获得的热力学量的微观表示式是必然的,按以上的分析,属于纯宏观理论的热力学量和热力学方程无法直接同微观理论挂钩,只得建立一套能同微观概念相联系的统计平衡态概念及统计平衡系统所遵从的方程。但是,我们的目的终究是建立热力学的微观理论,这就是说,还必须把统计平衡系统所遵从的方程同热力学方程连结起来。怎样才能把它们连结起来呢?迄今为止,所找到的唯一方法是:认定统计平衡态同热力学平衡态所反映的对象是一致的,它们所遵从的规律是相同的,因而表述形式相同的两类方程,实际上是分别从微观的角度和宏观的角度反映着同一规律,它们相对应的项可以一一进行比较,事实上,比较和联立两类方程的方法意外地解决了大多数热力学量不能同微观量联系起来的困难。所以,不少物理学家认为,两类方程相比较的方法是统计力学的一个基本精神,是统计力学的中心思想。
按形式逻辑知识,比较推理属或然推理,所得结果可能正确,也可能不正确,那么统计力学中的通过两类方程所进行的比较推理,所得结果为什么是正确的呢?显然,两类方程比较推理正确的原因,正是统计平衡态同热力学平衡态所反映的对象基本一致,两类方程反映着同一个规律。所以,可以说,两类方程比较推理是否正确,也是判别统计平衡态的定义是否正确的一个标准。
第六步 玻尔兹曼统计力学的运用
统计力学的运用可以分为两个主要的方面:(1)根据玻尔兹曼关系式S=K l nW给予热力学第二定律和第三定律以微观解释;(2)计算具体系统的热运动性质和规律。计算的统一方法便可以归纳四步:建立所研究系统的微观模型,写出微观粒子或系统状态的能量表达式;计算配分函数z;通过z计算各热力学量;讨论结果。至于计算的具体方法和过程,本文就不再赘述了。
此结构图不仅仅指出了玻尔兹曼统计力学体系的关节点和逻辑线索,如果联系每一步骤下的物理思想和方法,将有利于从中提取物理知识、物理思想和方法。
O414
A
1671-2862(2011)02-0109-04
2011-02-03
姜小兰,女,新乡广播电视大学讲师,研究方向:物理教学研究。

