平面几何视角下解三角形问题的四大模型
于 涛
广东省东莞市东莞中学 (523005)
平面几何视角下解三角形问题的四大模型
于 涛
广东省东莞市东莞中学 (523005)
模型一:点动
三角形固定一边(即确定了两个顶点),第三个顶点按照某种规律运动,称为点动.例如在ΔABC中,边BC=2,∠A=60°时,则点A在ΔABC的外接圆上运动.

A.{Sn}为递减数列
B.{Sn}为递增数列
C.{S2n-1}为递增数列,{S2n}为递减数列
D.{S2n-1}为递减数列,{S2n}为递增数列
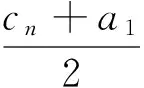
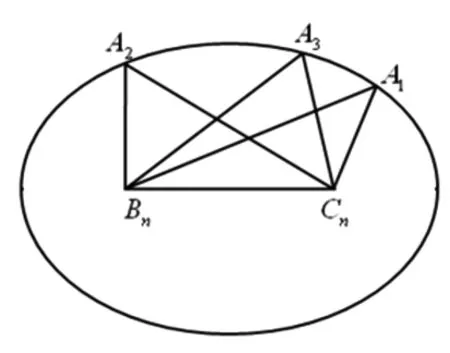
图1
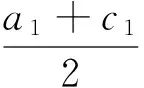
如图1,在边BnCn固定的情况下,所有三角形的底相同,而高的大小随着点Ai(i=1,2,3,…)的运动而变化.因为ΔAnBnCn中较大角越变越小,所以三角形的高越来越高,故{Sn}为递增数列.
评析:题目将三角形隐藏于数列背景,需要通过数列的推理演算,才能发现ΔAnBnCn中边BnCn为定值(即顶点Bn,Cn为定点),点An满足条件
|AnBn|+|AnCn|=2a1(即bn+cn=2a1).根据点动模型,便可发现点An在以Bn,Cn为焦点,2a1为定长的椭圆上运动,使得题目化繁为简.题目设计时,让第三点满足于椭圆的定义,据此发散思维,第三点还可以满足双曲线的定义,满足三角形外接圆的条件等,不论条件如何变化,均是固定两点,让第三点按照某种规律运动.
模型二:线动
三角形固定一个角的大小(即确定了两条边的方向),第三边的端点在已知角的两边上滑动,称为线动;以此类推,四边形固定相邻两个角的大小(即确定了相邻三条边的方向),第四边的端点在与其相邻的两边上滑动,也称为线动.
例2 (2015年全国Ⅰ卷理科)在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是___________.
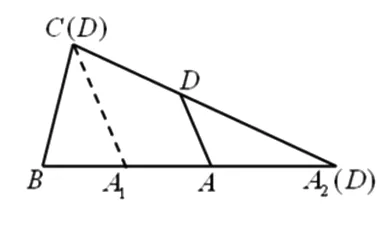
图2
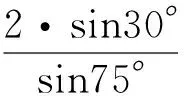
评析:题目固定了四边形ABCD中边BC的长及∠B,∠C的大小,即明确了边BA,CD所在的直线,因此点A,D分别在边BA,CD所在直线上滑动.已知∠A=75°,则边AD的方向也确定了,但长度不确定.根据线动模型,可发现四边形因边AD的平行滑动而变化,从而在变化过程中发现AB的变化.
模型三:角动
三角形固定一个角及其对边所在直线,角的两边与其对边的两个交点和角的顶点可确定三角形,以角的顶点为旋转点,随着角的旋转三角形发生变化,称为角动.
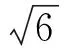
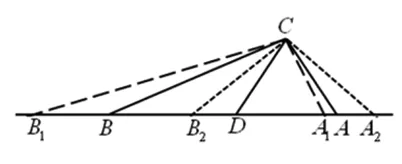
图3
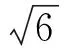
评析:题目固定了两个角,分别是∠ACB=120°和∠ADC=60°,两个角因CD=2而确定了点C的位置和边AB所在的直线,因此点A,B在该直线上运动并满足与点C形成∠ACB=120°.根据角动模型,以点C为旋转点,使∠ACB旋转,与边AB所在直线的交点为点A,B,明确了ΔABC的变化规律,从而在几何图形变化的过程中发现∠ACD的变化.
模型四:图形动
旋转变换与平移变换作为初中平面几何的重要思想方法,在高中平面几何问题中依然适用,称为图形动.

图4
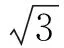
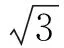
评析:题目几何图形中边长AC因角B的变化而变化,使得ΔACD随之变化,引起点D的运动.题目在条件设置时埋下了AC⊥CD及AC=CD的伏笔,在应用旋转变换时图形旋转的角度为90°,图形大小不变,当旋转ΔCBA至ΔCB′D时,便找到了点D的运动规律,让我们感受到“柳暗花明又一村”.
以上四种模型应用于不同特征的解三角形问题,由于高考题和模拟题解三角形综合问题难度较大,如果局限在高中所学解三角形与三角函数知识中,往往会因复杂的运算而导致求解失败.当解题跳出知识的局限,回归平面几何的本质时,则可以从几何要素点、线、角、图形等角度,将问题转化为观察变化规律的平面几何问题,化繁为简,避免了大量代数运算,缩短解题时间.当然平面几何视角下的解三角形问题具有较高的技巧性和特定性,需要在实际解题过程中多体会模型的特征,从而提高解三角形问题的几何意识.

