不同损失下k阶Erlang分布参数的Bayes估计

季海波

(宿迁学院 文理学院, 江苏 宿迁 223800)

0 引言

k阶Erlang分布的随机变量是k个独立的同参数的指数分布随机变量的和,它是一种Phase-Type分布,是亚指数分布的一个特例(各阶指数过程的均值都相等的k阶亚指数分布就是k阶Erlang分布),而指数分布是k阶Erlang分布的特例．相比于指数分布,k阶Erlang分布能更好地对现实数据进行拟合(更适用于多个串行过程,或者无记忆性假设不显著的情况下),故在排队论中被广泛应用,在保险金融中也被用作索赔分布,在不同损失下对其他分布参数的研究也不少[1-3],但国内对该分布的统计性质进行的研究不多．本文主要研究了在不同损失函数下k阶Erlang分布参数的Bayes估计．

定义1[4]若X1,X2,…,Xk是一列独立的随机变量,且都服从指数分布E(μ),则随机变量T=X1+X2+…+Xk具有概率密度

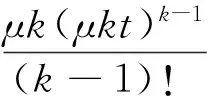
或者等价地,其分布函数为

称T服从参数为μ的k阶Erlang分布．

为便于估计,令θ=kμ,则k阶Erlang分布的密度函数和分布函数分别为

(1)

(2)

其中θ>0．

从k阶Erlang分布中抽取容量为n的简单样本T1,T2,…,Tn,记T(T1,T2,…,Tn),t(t1,t2,…,tn)为T的观测值,则样本t的似然函数为

(3)

1 不同损失函数下θ的Bayes 估计

引理1 设T=(T1,T2,…,Tn)是来自分布(1)的一个简单随机样本,若参数θ的先验分布取指数分布E(λ),λ>0,则θ的后验密度函数为

(4)

证明设参数θ的先验分布为E(λ),λ>0,则

π(θ)=λe-λθ(λ,θ>0),

样本t=(t1,t2,…,tn)关于θ的条件密度为

则参数θ的后验密度函数为

得证．

而在Bayes估计中,损失函数的选取将会对参数估计量的优良性有较大影响．下面将取不同的损失函数来得到参数θ的Bayes估计．

证明由文[5]及引理1,可得在平方损失函数L(θ,δ)=(θ-δ)2下

再由文[5],在给定的Bayes决策中,若在给定的先验分布下,θ的Bayes估计δ0(x)唯一且是容许的．

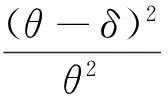
证明由文[3]及引理1,可得在二次损失函数下

由文[5]知,在给定的Bayes决策中,若在给定的先验分布下,θ的Bayes估计δ0(x)唯一且是容许的．

证明由文[3]中定理1定理2,可得在平衡损失函数下

由文[5]知,在给定的Bayes决策中,若在给定的先验分布下,θ的Bayes估计δ0(x)唯一且是容许的．

定理4 在Linex损失函数L(θ,δ)=ec(δ-θ)-c(δ-θ)-1,(c∈R,c≠0)下,若参数θ的先验分布为E(λ),λ>0,则分布(1)中参数θ的Bayes估计为

从而

由文[5],在给定的Bayes决策中,若在给定的先验分布下θ的Bayes估计δ0(x)唯一且是容许的．

证明由文[6]及引理1,可得在熵损失函数下

由文[5],在给定的Bayes决策中,若在给定的先验分布下,θ的Bayes估计δ0(x)唯一且是容许的．

证明由文[7]及引理1,可得在对称熵损失函数下

由文[5],在给定的Bayes决策中,若在给定的先验分布下,θ的Bayes估计δ0(x)唯一且是容许的．

2 超参数λ的估计

对于k阶Erlang分布的密度函数用(1)式,取指数分布为参数θ的先验分布,则其边缘分布为

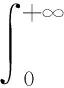
则似然函数为

令

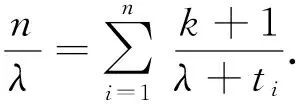
令

且

所以函数h1(λ)在(0,+∞)是严格单调递减的下凸函数．

所以函数h2(λ)在(0,+∞)内也是严格单调递减的下凸函数．

从而方程

在(0,+∞)内有唯一解,迭代公式为

(5)

3 Monte Carlo随机模拟

表1 参数估计的均值与均方误差

上述模拟结果表明:

1) 参数θ的Bayes估计的均方误差明显比极大似然估计的均方误差要小,所以极大似然估计的效果稍差．随着样本容量的增大,极大似然估计值越来越靠近真值,而且均方误差也越来越小,这体现出来了极大似然估计的大样本优越性．

2) 在Linex损失下,参数c的符号对θ的Bayes估计的差别并不大;从均方误差看,当样本容量为30和100时,都是对称熵损失下的均方误差最小,而在样本容量为50时,平方损失下的均方误差最小;从参数θ的估计值与真值的接近程度看,平衡损失函数下θ的估计是最接近的．

因此,由模拟结果所得出的结论可以通过选取的样本容量的大小来选取不同的估计．当样本容量不是很大时尽量选取Bayes估计从而提高估计的精度,容量很小或者较大时优先考虑对称熵损失下的Bayes 估计,容量中等时考虑选用平方损失下的Bayes 估计;从估计值与真值的接近程度看,优先考虑平衡损失下的Bayes 估计．

[1] 姚惠,谢林.不同损失下Lomax分布形状参数的Bayes估计[J].数学杂志,2011,31(6):1131-1135.

[2] 龙兵.不同损失函数下艾拉姆咖分布参数的Bayes 估计——全样本情形[J].重庆师范大学学报(自然科学版),2013,30(5):96-100.

[3] 孙玉莹,王德辉.不同损失函数下偏正态分布的Bayes估计[J].吉林大学学报(理学版),2012,50(4):638-646.

[4] 胡运权等.运筹学基础及应用[M].北京:高等教育出版社,1986.

[5] 茆诗松,王静龙.高等数理统计[M].北京:高等教育出版社,1998.

[6] 肖小英,任海平.熵损失函数下两参数Lomax分布形状参数的Bayes估计[J].数学的实践与认识,2010,40(5):227-230.

[7] 周明元. 对称熵损失函数下两参数Lomax分布形状参数的Bayes估计[J].统计与决策,2010(12):161-162.

[8] 茆诗松.贝叶斯统计[M].北京:中国统计出版社,1999.

[9] James O Berger.统计决策论及贝叶斯分析[M].(2版).北京:中国统计出版社,1998.