不完备概率信息下可靠性分析的随机响应面法
缑变彩, 张 天, 王 帆
(1. 武汉科技大学 城市学院, 湖北 武汉 430083; 2. 武汉工程大学 资源与土木工程学院, 湖北 武汉 430073)
土体抗剪强度参数具有较强不确定性,需要采取可靠性分析手段估计隧道、边坡等岩土结构的失效概率,从而为设计及施工提供决策依据。常用的可靠性分析方法包括FORM、SORM和蒙特卡罗模拟等[1]。
然而在实践中采用上述方法进行可靠性分析时常常会遇到两个难点。第一个难点在于隐性极限状态方程的显性化表达,通常采用响应面法进行极限状态曲面的刻画,如采用二次多项式[2]、神经网络[3]、Kriging模型[4]等。然而传统的响应面法是一种侵入式算法,需要与原有数值模型进行联合迭代运算。为提高计算效率,目前常采用随机响应面法构建响应面方程。相比传统响应面法,随机响应面[5]属于非侵入式算法,其采用Hermite多项式在随机空间内对系统响应进行拟合,因此基于随机响应面法构建的替代模型可直接用于相关可靠性分析。
第二个难点在于概率信息的获取。可靠性分析需要知道随机变量的联合概率分布函数。而实上,受限于试验条件等难以准确获取该联合概率分布函数。相比之下,工程实践中较易获取的是随机变量的边缘分布及随机变量之间的相关系数。当随机变量相互独立时,随机变量的联合概率分布函数为其边缘分布函数的简单乘积;但当随机变量之间存在相关关系时,基于边缘分布及相关系数不能唯一确定相应的联合概率分布函数[6],因此该概率信息也被称之为不完备概率信息[7]。基于不完备概率信息的可靠性分析常采用Nataf变换获取标准随机空间与原随机空间的映射关系,如Li等[8]采用Nataf变换获取随机响应面配点在原随机空间内的位置以构建替代模型。但目前已证明Nataf变换实际上隐含假设随机变量之间的相关结构为高斯相关结构[9]。换言之,其结果仅仅只是众多可能结果中的一种,因此有必要研究当随机变量之间的相关结构为非高斯相关结构时的岩土结构可靠性。
本文提出了不完备概率信息下可靠性分析的随机响应面法,采用Copula理论建立随机变量的联合概率分布函数,基于Rosenblatt变换实现非高斯相关结构下随机响应面在原随机空间的配点选择,最后通过两个案例研究了不同相关结构对可靠性的影响。
1 基于配点的随机响应面法
1.1 随机响应面法基本原理
随机响应面法一般采用Hermite多项式进行拟合。设Y是输出随机变量,X=[x1,x2, …,xn]是n维输入随机变量,U=[U1,U2, …,Un]是相互独立的标准正态随机向量,且X=T(U)表示U到X的等概率变换,则极限状态Y=G(X)可表示为:
Y=G(X)=G(T(U))=H(U)
(1)
其中Y=H(U)为Hermite多项式:
(2)
式中:ai1i2…in为待定系数,Γp(·)为p阶Hermite多项式:
Γp(Ui1,Ui2,...,Uip)
(3)
理论上,随机响应面的拟合精度随着阶数p的增加而增加;然而高阶Hermite多项式将会导致展开项的快速增长。因此,通常需要对式(2)进行截断。表1列举了从2阶到4阶的Hermite多项式的展开形式。

表1 2~4阶Hermite多项式的展开形式
Li等[8]总结了建立随机响应面模型的四个主要步骤:(1)通过独立标准正态随机变量表示输入随机变量;(2)使用Hermite多项式表示输出随机变量;(3)确定Hermite多项式的系数;(4)用蒙特卡罗模拟等方法估算失效概率。其中建立随机响应面模型的关键在于第三步即确定Hermite多项式的系数,其求解方法包括Galerkin法和配点法。相较于Galerkin法,配点法操作简便,其有效性不受原响应面的非线性和复杂性影响,且配点相互独立,可同时计算每个配点对应的系统响应值。因此,本文采用配点法建立随机响应面模型。
1.2 配点的选择
构建随机响应面的关键在于求解待定系数ai1i2…in,可通过配点法确定,其基本原理是,对于p阶Hermite多项式,采用p+1阶Hermite多项式的根来确定标准随机空间内的输入随机变量,然后,通过等概率变换将这些配点从标准随机空间转换到原随机空间中,再采用传统结构分析方法确定这些配点所对应的系统响应值,最后通过下式求解待定系数:
a=(HTH)-1HTF
(4)
式中:H和F分别为基于配点给出的Hermite多项式矩阵和配点对应的系统响应值所构成的向量。
p阶Hermite多项式的根的数量也为p个,而p阶Hermite多项式的可选配点是p+1阶Hermite多项式根的组合,因此对于n维问题,p阶随机响应面的可选配点数量应为(p+1)n。Mollon等[10]注意到对于奇数阶随机响应面,原点不在可选配点之中,但考虑到原点在标准随机空间中占据高概率密度区域,因此需要将原点也作为可选配点之一,于是可选配点的数量Ncp为:
(5)
如果选取所有的候选配点来确定Hermite多项式系数,那么当n和p较大时就必须进行大量的结构分析来确定配点所对应的系统响应。实际上,确定系数所需的最小配点数目是:
(6)
一般地,Na远小于Ncp。因此,合理选择配点可以大大减少结构分析的工作量。对于低维问题,可以通过确保H为满秩矩阵的方法来选取配点[8]。
在确定Hermite多项式系数的过程中需要将配点从标准随机空间映射到原随机空间中,以便确定配点对应的系统响应。对于输入随机变量相互独立的情况,可直接通过解析的方式进行表达[5];对于输入随机变量之间存在相关关系且相关结构为高斯相关结构的情况,Li等[8]则给出了基于Nataf变换的映射方法;而对于不完备概率信息下非高斯相关结构的相关随机变量的配点映射将在下一节进行讨论。
2 不完备概率信息下非高斯相关结构随机变量的配点映射
不完备概率信息条件下的配点映射其难点在于联合概率分布模型的构建。根据Sklar理论,一个二维联合概率分布可以表示为该分布的边缘分布和一个Copula函数:
F(x1,x2)=C(u1,u2,θ)
(7)
式中:u1=F(x1)和u2=F(x2)分别为随机变量x1和x2的边缘分布函数;C为Copula函数;θ是Copula函数的参数。
相应的联合概率分布函数如下所示:
=c(u1,u2,θ)f1(x1)f2(x2)
(8)
式中:f1(x1)和f2(x2)分别为x1和x2的边缘概率密度函数,c(u1,u2,θ)是Copula密度函数。
当已知随机变量间的Pearson相关系数ρ时,Copula参数θ可以用下式来确定:
(9)
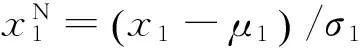
可见,给定某一特定copula函数,则二维联合概率分布函数可以基于其边缘分布和相关系数构造。特别的,当Copula函数取Normal时,所对应的二维联合概率分布函数为Nataf分布,而Nataf变换实际上就是假设联合概率分布为Nataf分布下的等概率变换。
由于Nataf变换仅适用于高斯相关结构的随机变量,因此本文在建立联合概率分布函数之后,采用Rosenblatt变换作为配点映射的方法。对于二维问题,Rosenblatt变换为:
(10)
式中:Φ-1(·)为标准正态分布累积分布函数Φ(·)的反函数;F(x2|x1)为边缘条件分布,可由下式表示:
(11)
式中:h(u2,u1,θ)为条件Copula函数。表1列举了一些常用Copula函数及相应的条件Copula函数。因此,采用Rosenblatt变换的逆变换即可实现配点从标准随机空间到原随机空间的映射X=T(U):
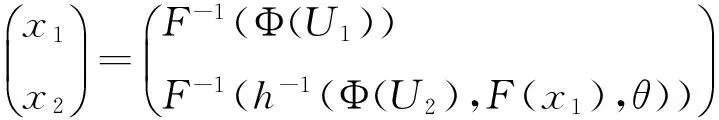
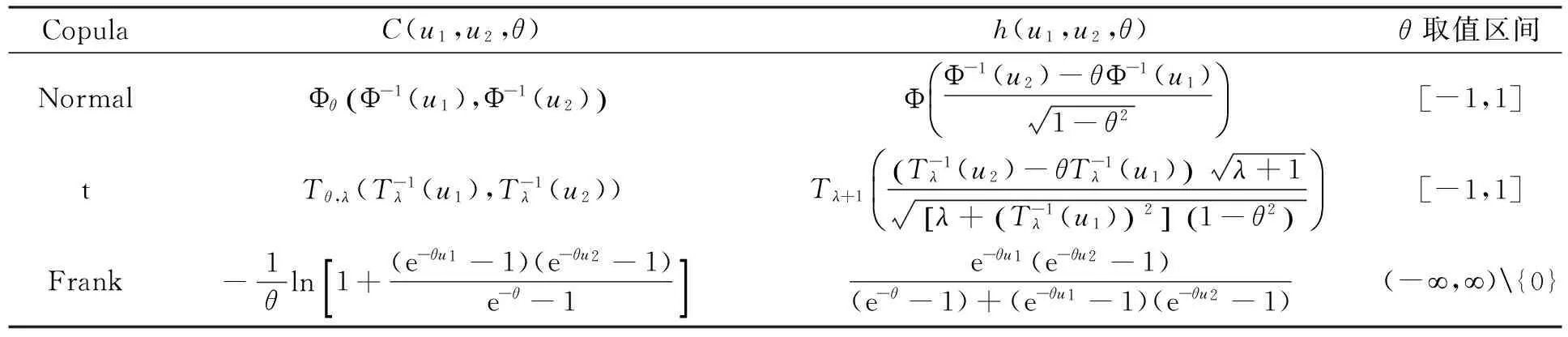
(12)
注:Φθ为相关系数为θ的二维标准高斯分布;Tθ,λ为相关系数为θ且自由度为λ的二维标准t分布;Tλ为自由度为λ的一维标准t分布
3 算例1
算例1研究如图1所示的某一静水压力场下圆形隧道的开挖可靠性。假设岩体是同质、均匀和连续的,静水压力场为p0,若开挖一半径为R的隧道,则塑性区半径Rpl为:
(13)
(14)
(15)
(16)
式中:c和φ分别为粘聚力和内摩擦角;pi为支护压力。
假设p0=2.5 Mpa,pi=0.1 Mpa,c和φ为随机变量,其统计分布如表3所示,并假设c和φ之间的相关系数ρ=-0.5。
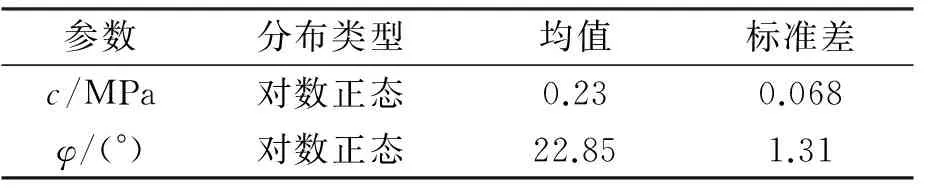
表3 算例1 随机变量的分布
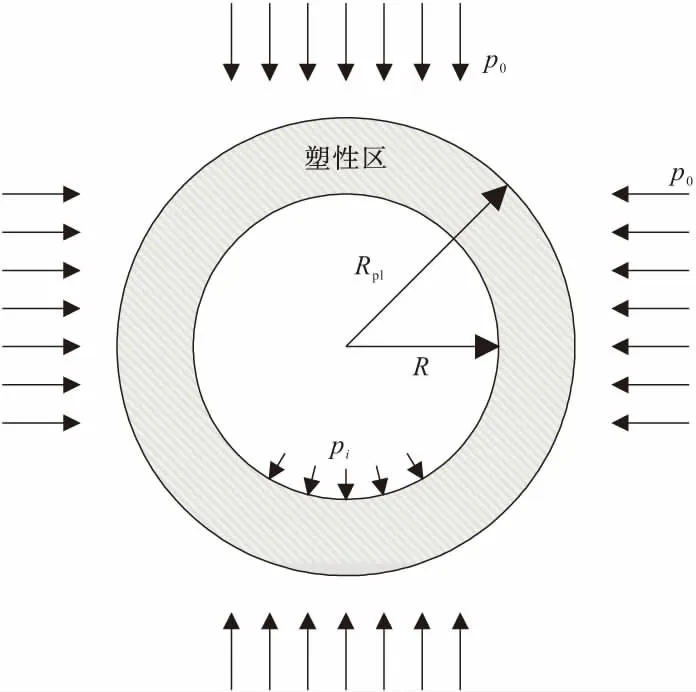
图1 隧道开挖示意
假设允许的塑性区半径为3倍洞径,则功能函数为:
(17)
首先假设c和φ之间的相关结构为高斯相关结构即Normal Copula,分别建立2~4阶隧道开挖塑性区半径的随机响应面,然后基于该随机响应面通过蒙特卡洛模拟(N=105)得出塑性区半径的分布。图2表示的是塑性区半径的累积概率函数(图中:y为允许的相对塑性区半径),为便于验证本方法,同时将基于Nataf变换并直接采用蒙特卡洛方法(N=105)得出的结果进行比较。注意建立2~4阶随机响应面时采用原解析模型进行隧道塑性区半径计算的次数分别为6,10,15次,其后蒙特卡洛模拟只是简单的代数计算,而直接采用蒙特卡洛模拟需要调用原模型105次。
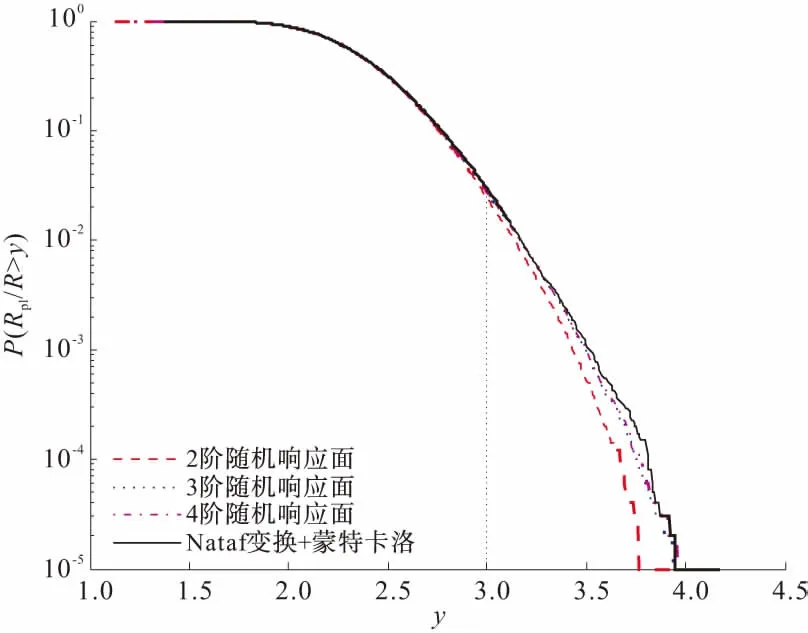
图2 隧道开挖塑性区半径的累计概率函数
表4比较了不同方法下基于式17的隧道开挖失效概率。若以Nataf变换加直接采用蒙特卡洛方法得出的结果作为精确解,则3阶随机响应面所对应的结果已具备较高精度。
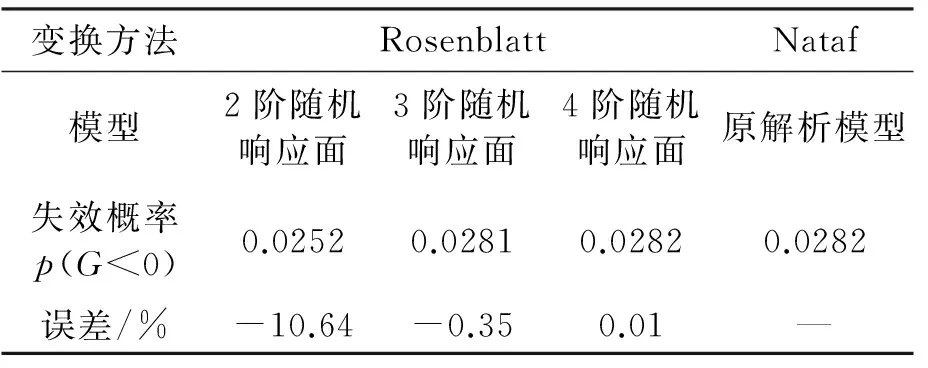
表4 高斯相关结构下可靠性分析结果对比
上述结果是假设c和φ之间的相关结构为高斯相关结构,然而实际上该假设并不一定成立,为检验非高斯相关结构是否对隧道开挖可靠性存在较大影响,本文分别研究了当相关结构用t Copula (λ=2)和Frank Copula表示时的隧道开挖失效概率。
图3对比了基于3阶随机响应面的不同相关结构下隧道塑性区半径分布的累积概率函数曲线。可以发现,不同相关结构对可靠性分析结果有着显著影响。表5比较了具体的失效概率以及相较于高斯相关结构时非高斯相关结构对应失效概率的偏差。可以看出当分别假设相关结构需要用t Copula (λ=2)和Frank Copula来表示时,基于高斯相关结构假设得出的隧道失效概率会明显高于或低于实际的失效概率,相对偏差分别为-10.61%和6.76%。因此,基于高斯相关结构假设有可能导致过于保守或过于冒进的施工及设计方案。
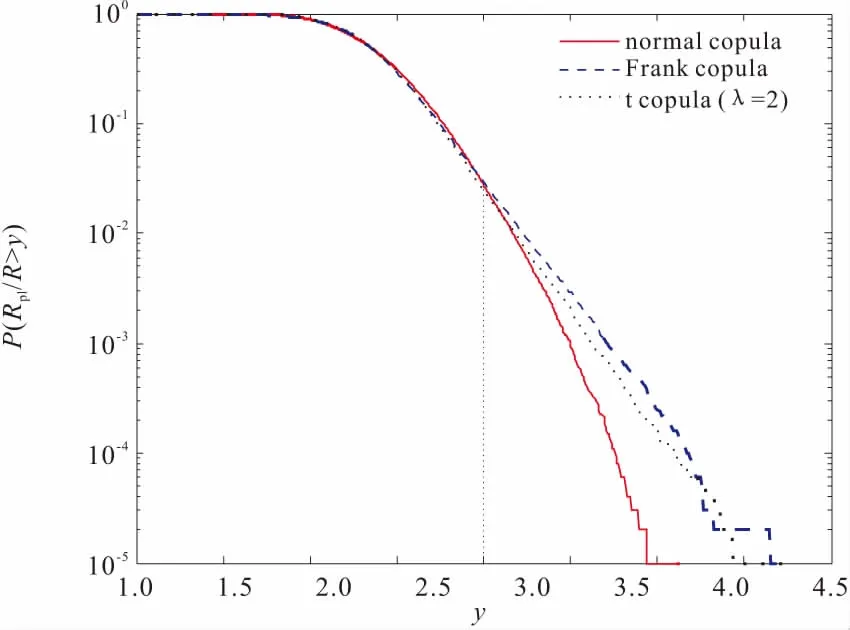
图3 隧道开挖塑性区半径的累计概率函数

Copula(相关结构)Normal(高斯)tCopula(λ=2)Frank失效概率p(G<0)0.02810.02540.0300偏差/%—-9.616.76
4 算例2
算例2研究如图4所示的某1∶1边坡,边坡高度10 m。土体抗剪强度参数即有效粘聚力c和内摩擦角φ均为随机变量,且服从表6给出的分布,相关系数ρ=-0.458,土体重度假设为常数。
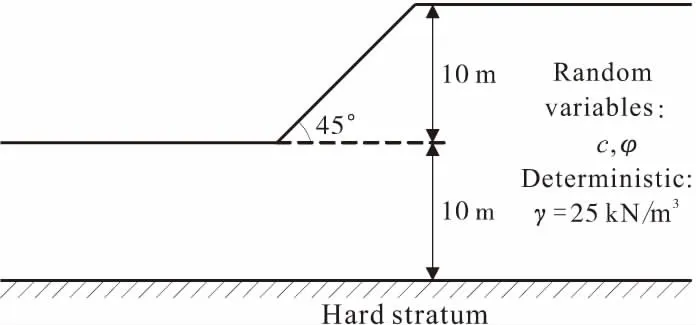
图4 边坡稳定性示意

参数分布类型形状参数比例参数c/kPaWeibull1.8658.24φ/(°)Gamma16.981.19
边坡稳定性分析是典型的隐性极限状态函数问题,其稳定性通常用安全系数FS表示,含义为潜在滑动面上的土体抗剪强度与滑动荷载的比值。边坡稳定性分析中极限状态函数为隐性,其原因在于最小安全系数对应的滑动面未知,需要通过一定的搜索算法进行识别,而且土体抗剪强度参数变化时,该潜在滑动面的位置也可能发生变化。
这里采用Bishop法计算边坡安全系数,滑动面形状假设为圆弧形,通过网格搜索确定给定土体抗剪强度下边坡安全系数的最小值及其对应的滑动面。为验证所提出方法的有效性,基于Rosenblatt变换通过蒙特卡洛(N=104)产生不同相关结构下服从已知边缘分布和相关系数的土体抗剪强度参数样本,然后直接采用边坡稳定性计算模型算出样本所对应的安全系数的分布,之后采用随机响应面法计算边坡的失效概率并与蒙特卡洛方法进行对比。
表7给出了该边坡可靠性分析的对比结果,基于随机响应面法得出的失效概率与蒙特卡洛所得出的结果基本一致。但是随机响应面法对原解析模型调用的次数远低于直接采用蒙特卡洛法调用原模型的次数。在本例中,基于5阶随机响应面对原模型的调用次数仅为21次,之后边坡安全系数的计算只需通过Hermite多项式进行简单的代数计算即可,总耗时约15 s左右,而采用样本数为10000的蒙特卡洛模拟则需要1小时以上。相关结构对于边坡失效概率仍有较大影响。当层状土有效粘聚力相关结构为Frank时,若仍基于Gauss相关结构(Nataf变换)进行分析会明显低估边坡失效概率,从而造成过于经济的设计。
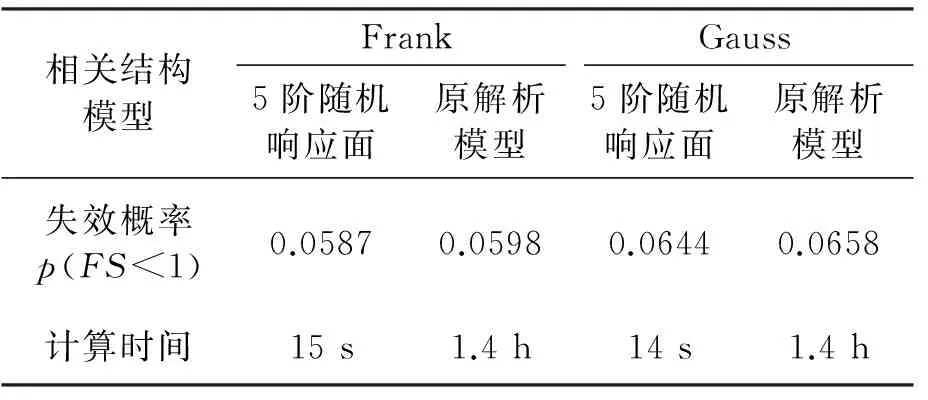
表7 边坡可靠性分析结果对比
5 讨 论
为研究相关结构如何影响可靠性分析结果,以案例1为例,图5a,5b分别显示了不同相关结构下3阶随机响应面配点在标准随机空间和原随机空间的位置(图中,U1,U2分别表示标准正态空间中的c和φ)。可以看出在标准随机空间中,候选配点和基于满秩矩阵实际选取的配点是相同的,不依赖于随机变量之间的相关系数和相关结构;但是当配点从标准随机空间向原随机空间进行映射时,由于c和φ之间存在负相关关系,因此在原随机空间中配点位置相较于标准随机空间进行了旋转,但不同相关结构(Copula)对该旋转有着一定影响,除原点外的所有配点在旋转时均有不同程度的偏移,而且配点距离原点越远,不同相关结构对于该配点旋转后位置的影响越大。因此,在假设不同相关结构时,同样的配点最后对应的系统响应值会有所不同,进而导致了随机响应面待定系数发生改变,从而得出不同的可靠性分析结果。
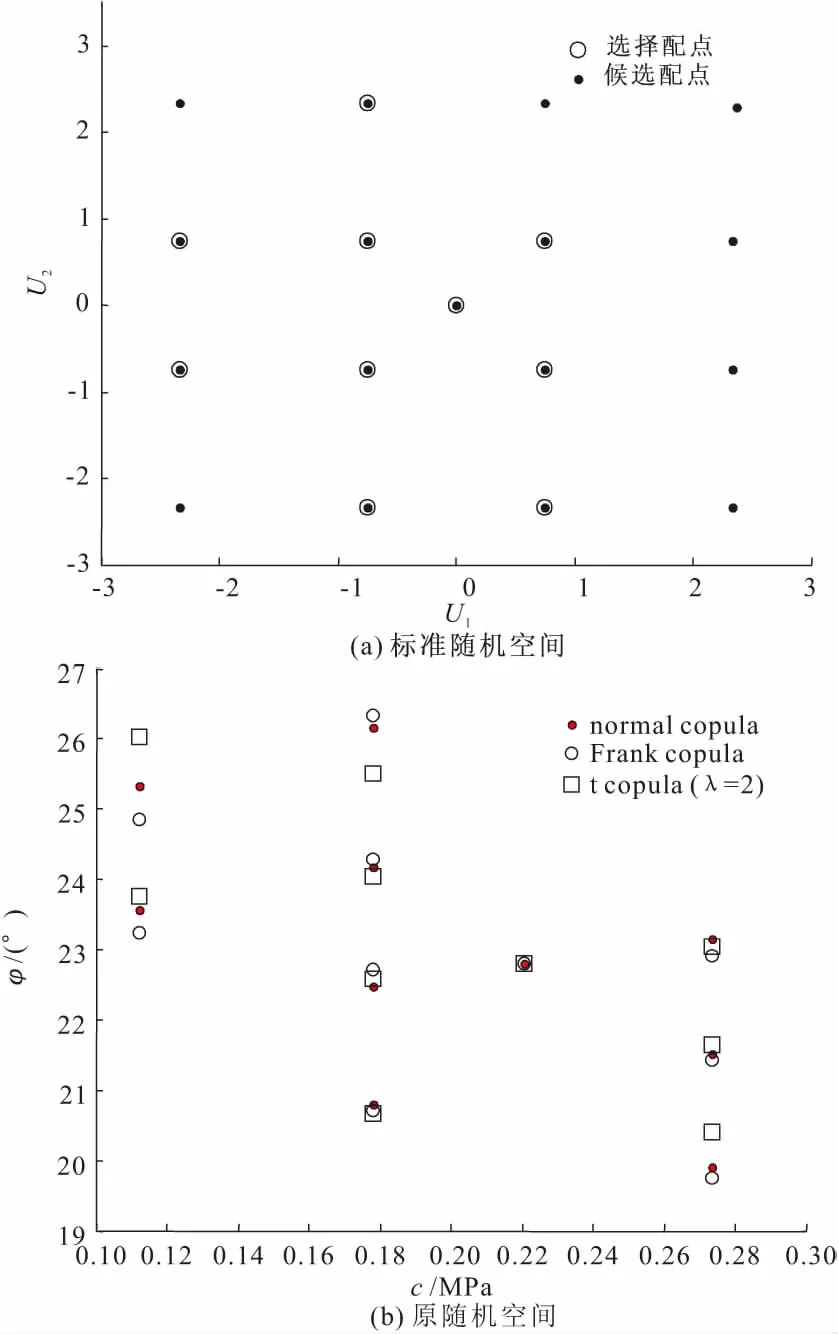
图5 3阶随机响应面配点的位置
由于相关结构可能对可靠性结果产生明显的影响,选择合适的Copula函数来表征随机变量之间的相关结构显得尤为重要。然而,在缺少实测数据的情况下难以准确确定变量之间的相关结构。因此,在给定随机变量的边缘分布和相关系数的条件下,需要补充有关相关结构信息。例如,若已知变量之间存在非对称的下尾相关性,则可以采用Clayton Copula计算失效概率,而不必受限于高斯相关结构假设的限制。
如果缺少相关结构的信息,可以检验不同非高斯相关结构相比高斯相关结构对应的可靠性结果偏差。如果偏差较大,再补充数据用于准确界定变量之间的相关结构或者直接选取较为保守的设计值。
6 结 论
本文研究了不完备概率信息下可靠性分析的随机响应面方法,基于Copula理论建立了联合概率分布模型,通过Rosenblatt变换实现了配点从标准随机空间到原随机空间的映射,并以某圆形隧道开挖和某层状边坡为例探讨了不同相关结构对随机响应面构建及可靠性结果的影响,得出以下结论:
(1)当假设不完备概率信息条件下变量之间的相关结构为高斯相关结构时,基于Nataf变换和基于Ronsenblatt变换得出的可靠性结论是一致的,说明两种等概率变换形式在假设Normal Copula时是等效的;
(2)随机响应面可以较为精确地将原有隐性功能函数显性化,但不完备概率信息下随机变量之间的相关结构未知,而假设不同相关结构对于可靠性结果有着较为显著的影响,常用的高斯相关结构会明显低估或高估系统的失效概率进而导致过于保守或过于经济的设计和施工方案;
(3)不同相关结构即Copula选择对于可靠性分析结果的影响是通过改变配点在原随机空间中的位置来实现的,除原点外的所有配点在映射后均有不同程度的偏移,而且配点距离原点越远,不同相关结构对于该配点旋转后位置的影响越大,从而导致相同的配点却对应不同的系统响应值并影响可靠性分析结果。
[1] Ditlevsen O, Madsen H O. Structural Reliability Methods[M]. Chichester : John Wiley & Sons Ltd, 2007.
[2] Xu B, Low B K. Probabilistic stability analyses of embankments based on finite element method[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(11): 1444-1454.
[3] Cho S E. Probabilistic stability analyses of slopes using the ANN-based response surface[J]. Computers and Geotechnics, 2009, 36(5): 787-797.
[4] Luo X, Li X, Zhou J, et al. A Kriging-based hybrid optimization algorithm for slope reliability analysis[J]. Structural Safety, 2012, 34(1): 401-406.
[5] Huang S P, Liang B, Phoon K K. Geotechnical probabilistic analysis by collocation-based stochastic response surface method: An Excel add-in implementation[J]. Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 2009, 3(2): 75-86.
[6] Tang X S, Li D Q, Rong G, et al. Impact of copula selection on geotechnical reliability under incomplete probability information[J]. Computers and Geotechnics, 2013, 49: 264-278.
[7] Der Kiureghian A, Liu P L. Structural reliability under incomplete probability information[J]. Journal of Engineering Mechanics, 1986, 112(1): 85-104.
[8] Li D, Chen Y, Lu W, et al. Stochastic response surface method for reliability analysis of rock slopes involving correlated non-normal variables[J]. Computers and Geotechnics, 2011, 38(1): 58-68.
[9] Lebrun R, Dutfoy A. An innovating analysis of the Nataf transformation from the copula viewpoint[J]. Probabilistic Engineering Mechanics, 2009, 24(3): 312-320.
[10]Mollon G, Dias D, Soubra A H. Probabilistic analysis of pressurized tunnels against face stability using collocation-based stochastic response surface method[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(4): 385-397.

