两个有界线性算子和的Drazin逆

杜 娟,王 华

(内蒙古工业大学理学院,内蒙古呼和浩特 010021)

1 引言与预备知识

广义逆理论是非常重要的研究领域之一,它在求解奇异微分和差分方程、算子方程、马尔可夫链、迭代法数值分析等方面都有着非常广泛的应用.特别在求解微分方程组时,矩阵的广义逆发挥着重要作用,例如给定一类一阶奇异系统方程

其中A为奇异矩阵.其通解可表示为

其中 A1=(λA+B)−1A,B1=(λA+B)−1B[1].

20世纪以来,学者们对广义逆理论中的矩阵的Drazin逆的研究最为活跃.1958年,Drazin[2]在半群与结合环上引入Drazin逆,并在两个矩阵P和Q满足PQ=QP=0的条件下,证明出了(P+Q)D=PD+QD.对于算子情形,2009年,Castro-Gonz´alez[3]等在P2Q=PQ2=0条件下讨论了P+Q的Drazin可逆性,并给出了(P+Q)D的表达式;同年,邓春源[4]在P,Q均为幂等算子,且满足三个不同条件PQP=0,PQP=PQ,PQP=P时给出了(P+Q)D的表达式;2011年,Cvetkovi´c[5]等在PQP=0,Q2P=0的条件下,给出了(P+Q)D的表达式;2014年,黄俊杰[6]等在P2Q+PQ2=0,P3Q=PQ3=0的条件下给出了(P+Q)D的表达式.对于P,Q为矩阵情形，学者魏益民[7]、Hartwig[8]、卜长江[9]、刘喜富[10]等获得了很多好的结果.

为便于叙述,文中通篇采用如下的假设及符号.设X,Y是复Banach空间,记B(X,Y)是从X到Y的所有有界线性算子的集合;B(X)是从X到X的所有有界线性算子的集合;对于A∈B(X,Y),ρ(A),σ(A),r(A)分别表示其预解集,谱集,谱半径;R(λ,A)表示算子A的预解式 (λI − A)−1.

下面给出本文用到的定义和引理.

定义1.1设A∈B(X),若存在AD∈B(X),使得算子方程组

对某个非负整数k成立,则称A是Drazin可逆的.对于上述方程组,若有解,则解必定唯一,这个唯一的解AD称为A的Drazin逆,并称使得方程组成立的最小非负整数k为A的指标,记为ind(A).当ind(A)=0时,A是可逆的,即AD=A−1.

引理1.2[11]设A∈B(X,Y),B∈B(Y,X),如果BA为Drazin可逆,那么AB也为Drazin可逆,且

引理1.3[12]设A∈B(X),则AD存在当且仅当0∈ρ(A)或0∈σ(A)为预解式R(λ,A)的一个极点,此时有

其中0＜ |λ|＜(r(AD))−1,Aπ=I−AAD,I是单位算子.

注由引理1.3可知,A的Drazin逆AD就是R(λ,A)的Laurent展开式中−λ0的系数,即

2 主要结果

引理2.1设P,Q∈B(X,Y)均是Drazin可逆的,且ind(P)=t,ind(Q)=s.若P5Q=0,P2Q+PQ2=0,PQPQ=0,则

其中 0 ＜ |λ|＜ min((r(PD))−1,(r(QD))−1), Δ(λ)= λI − Q − R(λ,P)PQ.

证 由P5Q=0,知PDQ=0,进而PπPQ=PQ.再由P2Q+PQ2=0,知

从而当 0 ＜ |λ|＜ (r(PD))−1时,由 (1.1)式,知

注意到PQ3=P3Q,PQPQ=0,可知PQ3PQ=P3QPQ=0.由此

由(PQ)2=0以及(PQ3)2=0,知PQ,PQ3是Drazin可逆的,且(PQ)D=0,(PQ3)D=0,则

于是,当 0 ＜ |λ|＜ min((r(PD))−1,(r(QD))−1)时,

结论得证.

其中 0 ＜ |λ|＜ min((r(PD))−1,(r(QD))−1).

证令 ρ(Δ)={λ ∈ C:Δ(λ)可逆}.显然,ρ(M)Tρ(P)= ρ(P)Tρ(Δ).则当 λ ∈ρ(M)∩ρ(P)时,

由(2.3),(2.1),(2.2)式,以及PQPQ=0,有

于是,便有

引理得证.

引理2.3设P,Q∈B(X,Y)均是Drazin可逆的,且ind(P)=t,ind(Q)=s.若P5Q=0,P2Q+PQ2=0,PQPQ=0,则下列结论成立.

(i)R(λ,Q)R(λ,P)的Laurent展开式中−λ0的系数为

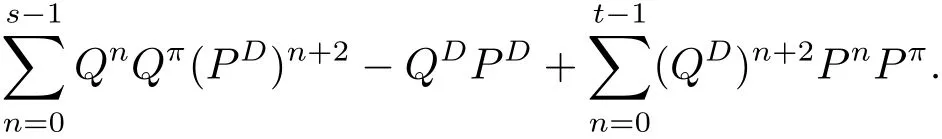
(ii)λ−2R(λ,Q)PQR(λ,P)的 Laurent展开式中 −λ0的系数为

(iii)λ−4R(λ,Q)PQ3R(λ,P)的 Laurent展开式中 −λ0的系数为

(iv)R(λ,Q)(I+λ−2PQ+λ−4PQ3)R(λ,P)的Laurent展开式中−λ0的系数为U−V+W,其中

证根据R(λ,P)和R(λ,Q)的Laurent展开,即可得到(i),(ii),(iii)中的结论.又注意到

这样便由(i),(ii),(iii)可得结论(iv).

定理2.4设P,Q∈B(X,Y)均是Drazin可逆的,且ind(P)=t,ind(Q)=s.若P5Q=0,P2Q+PQ2=0,PQPQ=0,则P+Q是Drazin可逆的,且

其中U,V,W见引理2.3.

注意到 (I+ λ−2PQ+ λ−4PQ3)R(λ,P)和 R(λ,Q)(I+λ−2PQ+λ−4PQ3)的 Laurent展开式中−λ0的系数分别为PD+PQ(PD)3+PQ3(PD)5和QD+(QD)3PQ+(QD)5PQ3.于是,由引理1.3和引理2.2,有

由PDQ=0,PQD=0,以及PPD=PDP知

定理得证.

由定理2.4,有如下推论.

推论2.5设P,Q∈B(X,Y)为Drazin可逆,且ind(P)=t,ind(Q)=s.若PQ=0,则

推论2.6设P,Q∈B(X,Y)为Drazin可逆,且ind(P)=t,ind(Q)=s.若P5Q=0,P2Q+PQ2=0,PQP=0,则

推论2.7设P,Q∈B(X,Y)为Drazin可逆,且ind(P)=t,ind(Q)=s.若P5Q=0,P2Q+PQ2=0,QPQ=0,则

推论2.8设P,Q∈B(X,Y)为Drazin可逆,且ind(P)=t,ind(Q)=s.若P3Q=0,P2Q+PQ2=0,PQPQ=0,则

3 应用

定理3.1若A2B=ABCB=CBCB=0,CAB+DCB=0,则算子矩阵M 是Drazin可逆的,且

其中

由此,根据已知条件,有P3Q=0,P2Q+PQ2=0,PQPQ=0.又由引理1.4,有

定理得证.

推论3.2[14]若A2B=0,BCB=0,CAB=0,DCB=0,则

推论3.3若A2B=CB=CAB=0,则

推论3.4[15]若AB=CB=0,则

参考文献

[1]Campbell S L.The Drazin inverse and systems of second order linear differential equations[J].Linear Multi-linear Alg.,1983,14:195–198.

[2]Drazin M P.Pseudoinverses in associative rings and semigroups[J].Amer.Math.Month.,1958,65:506–514.

[3]Castro-Gonz´alez N,Dopazo E,Martlnez-Serrano M F.On the Drazin inverse of the sum of two operators and its application to operator matrices[J].Math.Anal.Appl.,2009,350:207–215.

[4]Deng C Y.The Drazin inverse of the sum and difference of idempotents[J].Linear Alg.Appl.,2009,430:1282–1291.

[5]Cvetkovi´c A S,Milovanovi´c G V.On Drazin inverse of operator matrices[J].Math.Anal.Appl.,2011,375:331–335.

[6]Huang J J,Shi Y F,Chen A.Additive results of the Drazin inverse for bounded linear operators[J].Compl.Anal.Oper.The.,2014,8:349–358.

[7]Hartwig R E,Wang G R,Wei Y M.Some additive results on Drazin inverse[J].Linear Alg.Appl.,2001,322:207–217.

[8]Patricio P,Hartwig R E.Some additive results on Drazin inverses[J].Appl.Math.Comput.,2009,530–538.

[9]Bu C J,Feng C C,Bai S Y.Representations for the Drazin inverses of the sum of two matrices and some block matrices[J].Appl.Math.Comput.,2012,218:10226–10237.

[10]Yang H,Liu X F.The Drazin inverse of the sum of two matrices and its applications[J].Comput.Appl.Math.,2011,235:1412–1417.

[11]Wang G R,Wei Y M,Qiao S Z.Generalized inverses:theory and computations[M].Beijing:Grad.Ser.Math.Sci.Press,2003.

[12]Caradus S R.Operators theory of the generalized inverse[M].Queen’s Papers Pure Appl.Math.,Vol.38,Queen’s Univ.,Kingstom:Ontario,1974.

[13]Meyer C D,Rose N J.The index and the Drazin inverse of block triangular matrices[J].SIAM J.Appl.Math.,1977,33:1–7.

[14]Abdul Shakoor.矩阵和、分块矩阵与修正矩阵的Drazin逆[D].重庆:重庆大学,2014.

[15]Cvetkovi´c-Ili´c D S.A note on the representation for the Drazin inverse of 2 × 2 block matrices[J].Linear Alg.Appl.,2008,429:242–248.

[16]Huang J J,Shi Y F,Alatancang.The representation of the Drazin inverse of anti-triangular operator matrices based on resolvent expansions[J].Appl.Math.Comput.,2014,242:196–201.

[17]Cui R P,Li X L,Gao J L.The Drazin inverse of a modi fied matrix A−CB[J].J.Math.,2014,34(1):12–16.