一道能让“隐圆”大展身手的几何题*

●

(南京金陵中学河西分校,江苏 南京 210019)

原创题如图1，在△ABC中，∠ACB=90°，AC=BC，D为∠BAC的角平分线上一点，且∠BDC=67.5°，求证：CD=BC.

图1 图2

此题题干简练、图形清晰，看似不难，但提笔求解却并不容易，笔者先利用八年级的数学知识给出一种证法：

证法1因为∠ACB=90°，AC=BC，所以

∠BAC=∠ABC=45°.

如图2，作DE⊥AC于点E，DF⊥AB于点F，则

DE=DF， ∠FDE=135°，

又因为∠BDC=67.5°，所以

∠BDF+∠CDE=67.5°.

延长CE至点G，使得EG=FB，可得

Rt△DEG≌Rt△DFB(SAS)，

从而

DG=DB， ∠GDE=∠BDF，

于是∠GDC=∠GDE+∠CDE=67.5°=∠BDC.

又DC=DC，得△GDC≌△BDC(SAS)，从而

于是

∠DBC=67.5°=∠BDC，

故

CD=BC.

评注由角平分线上的点想到作“双垂线”非常自然，但后续的辅助线及两次全等三角形的证明，显然不易.能从其他角度求解吗？下面笔者利用“隐圆”再给出另5种较为简洁的证法，供读者参考.

证法2因为∠ACB=90°，AC=BC，所以

∠BAC=∠ABC=45°.

如图3，作△ABD的外接圆交AC的延长线于点E，则∠BDE=135°，从而

∠EDC=135°-67.5°=67.5°=∠BDC.

因为AD平分∠BAE，所以BD=ED，又DC=DC，于是

△BDC≌△EDC(SAS)，

从而

∠DBC=∠BDC，

故

CD=BC.

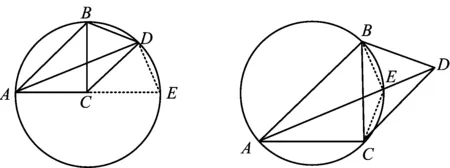
图3 图4

证法3因为∠ACB=90°，AC=BC，所以

∠BAC=∠ABC=45°.

如图4，作△ABC的外接圆交AD于点E，联结BE,CE，则

∠BEA=∠BCA=90°， ∠BED=90°，

∠BEC=135°=2∠BDC.

因为ED平分∠BAC，所以

BE=CE，

点E为△DBC的外心，可知

∠BCD=∠BED=45°，

从而

∠DBC=67.5°=∠BDC，

故

CD=BC.

评注这两种证法通过作出“隐圆”——三角形的外接圆，促成了角的关系显性化，特别是证法2，从作外接圆到产生新的“隐圆”，为问题的解决铺平了道路.

证法4因为∠ACB=90°，AC=BC，所以

∠BAC=∠ABC=45°.

如图5，设E为△ABC的内心，则点E在AD上，联结BE,CE，则BE平分∠BAC,CE平分∠ACB，可知

∠BEC=112.5°，

从而

∠BEC+∠BDC=180°，

因此点B,E,C,D共圆，从而

∠DBC= ∠DEC=∠EAC+∠ECA=

67.5°=∠BDC，

故

CD=BC.

图5 图6

证法5因为∠ACB=90°，AC=BC，所以

∠BAC=∠ABC=45°.

如图6，在AC的延长线上取点E，使得AE=AB，联结BE,DE，则

∠AEB=∠ABE=67.5°=∠BDC，

从而点B,C,E,D共圆，于是

∠BDE=180°-∠BCE=90°.

因为AD平分∠BAE，所以AD垂直平分BE，可得

BD=ED，

即

∠DBE=45°，

从而 ∠DBC=∠EBC+∠DBE=67.5°=∠BDC，故

CD=BC.

证法6因为∠ACB=90°，AC=BC，所以

图7

如图7，在AB上取点E，使得AE=AC，联结CE,DE，则

∠AEC=∠ACE=67.5°=∠BDC，

从而点B,E,C,D共圆，于是

∠CDE=∠ABC=45°.

因为AD平分∠CAE，所以AD垂直平分CE，可得

CD=ED，

从而

得

∠DBC=67.5°=∠BDC，

故

CD=BC.

评注这3种证法通过证明“隐圆”——四点共圆，使得角的关系更加密切，问题的解决也就水到渠成了.

这是一道难得一见的几何题.几种确定“隐圆”的常用方法在此大展身手，彰显了圆的独特魅力.图中无圆，心中有圆，难题不难.波利亚曾说过：“一个专心、认真备课的教师能够拿出一个有意义但又不太复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的理论领域.”在日常教学中善于发现、创造这样的问题，是教师专业发展的必修课，也是成为优秀数学教师的必由之路.