一种基于插值拟合的复杂刀具轨迹在线平滑压缩算法

陶　浩　何改云　王太勇　董甲甲　张永宾

天津大学机械工程学院，天津，300072

0　引言

在复杂曲线曲面的数控加工中，传统的刀具轨迹生成方法是通过CAM系统生成G01代码，再将其输入到数控系统中进行直线插补加工。该方法原理简单，但相邻线段的衔接处易出现速度和加速度的波动，从而显著降低零件的加工质量。为了减小速度和加速度的波动，吕强等［1］提出了通过限制相邻线段的衔接速度以实现速度平滑过渡的方法。近年来，随着直接参数曲线插补方法的提出和发展，已有许多学者证明参数曲线插补方法能满足目前数控加工行业高速高精的要求［2-5］。另外，相比G01代码而言，参数曲线的数据量非常小，节省了数控系统的内存空间。对于复杂曲线曲面的加工路径而言，现有的CAM系统仍以产生G01代码为主，因此，人们利用参数曲线对G01代码进行拟合［6-8］，不但可压缩数据量，还可从本质上平滑加工路径。无论是参数曲线插补还是拟合，NURBS和B样条曲线的应用最为广泛。

数据点的拟合方法一般分为两大类：插值拟合和逼近拟合。插值拟合精度较高，但不能缩减数据量；逼近拟合可大幅度缩减数据量，但为了在指定的精度内逼近给定的数据点，必须通过迭代的方法不断增加控制点（一般以最少的控制点个数开始拟合），因此逼近拟合效率极低。且当控制点和节点的数量增加后，某些节点区间可能为空，会导致在逼近拟合求解时出现奇异方程组的情况，需进一步特殊处理。此外，关于NURBS曲线拟合时如何设定权值的研究很少，大多数情况下，简单地将所有权值都取为1，即进行B样条拟合（B样条曲线实质上是控制点权因子均为1的NURBS曲线）。且实际上对逼近拟合来说，允许其选取任意的权因子可能会生成具有较少控制点的曲线；但对插值拟合来说，其控制点个数固定，没有合适的理由选取任意的权因子［9］。

YAU等［10］利用最小二乘法，将数据点逼近拟合成NURBS曲线。为了减少拟合时的数据量，PARK等［11］提出了对主导点进行拟合的方法。ZHANG等［12］同样提出了几何特征点的自适应查寻方法。ZHAO等［13］提出了根据离散点曲率和弦高误差等条件进行主导点选取的方法。TSAI等［14］提出了一种可实时具有C2连续性的局部Bezier曲线插值拟合方法，在逼近拟合时需计算数据点的拟合精度。传统的牛顿迭代法虽精度较高，但效率较低。ZHU等［15］推导出了加工过程中实时计算轮廓跟随误差的Taylor二阶展开算法，该算法可移植到数据点拟合时的精度校验过程中，其计算速度较快且能达到合理的控制精度。

本文综合主导点和局部Bezier快速插值拟合的方法，给出了主导点的确定方法，并在离线数据预处理阶段，通过局部Bezier插值拟合和精度校验不断增加新的主导点，最后对主导点进行在线插值拟合以及误差校验，拟合后的曲线只需对非主导点进行1次误差校验循环，就能达到预期的拟合精度要求，从而加快了拟合速度。

1　主导点的种类与选择

1.1　曲率极大值点和超过曲率阈值的点

很多文献指出，曲线的曲率值是用来判断曲线平滑性的一种有力工具［16］。但对于离散数据点而言，无法根据曲线的导数求取曲率的准确值。依据文献［17］提供的方法，离散数据点的曲率估算公式如下：

式中，Qi-1、Qi和 Qi+1为三个连续的数据点；KQi为点 Qi处的曲率估算值；A(Qi-1,Qi,Qi+1)表示Qi-1、Q和Qi+1三点构成的三角形的面积。

文献［18］提出了离散数据点曲率的另一种估算公式，通过推导发现，两套计算公式的本质一致。但文献［18］中的公式涉及反三角函数的求解，增加了计算的复杂性。

图1所示为对半蝴蝶状复杂曲线除去首末2点后的269个离散数据点的曲率估算结果。由图1可以看出，将连续曲线离散后进行曲率的估值计算，不可避免地会引起计算值的波动，在曲率较大处的效果尤为明显。为了更加准确地提取离散数据点的曲率极大值点，本文通过将当前曲率值点分别与前后5个连续相邻的曲率值点相比较，进而筛选出曲率极大值点（部分）。对于前后比较点个数的确定并没有严格的要求，但如果选取个数过少（前后至少各1个），则无法很好地排除数据波动点；而如果选取个数过多，可能会漏选一部分曲率极大值点（但在曲率值较大点处可通过曲率阈值点补选）。本文选定此数目为5，并将曲率极大值处的数据点标记为主导点。为了保证拟合曲线能够较好地进行插值或逼近曲率值较大处的数据点，除了曲率极大值点外，本文还设定了1个曲率阈值Km，若离散数据点的曲率值大于设定的曲率阈值Km，则同样将其标记为曲线拟合时的主导点。这也是本文不单纯使用当前曲率值点与前后较少数量（如2个）曲率值点作比较的原因，因为单纯应用曲率极大值点选取法且前后比较数量为2时，会漏选图1中的P1和P2点。

图1　半蝴蝶状复杂曲线离散数据点的曲率估算值Fig.1　Curvature estimation of discrete points of semi-butterfly curve path

1.2　曲线的拐点或反曲点

在数学上，曲线的拐点或反曲点是定义曲线凹凸性发生变化的转折点。对于3次Bezier曲线而言，其二阶导函数为一条直线，依据曲线拐点的判断原则，3次Bezier曲线内部最多只能有1个拐点，因此，在利用3次Bezier曲线对离散数据点进行逼近拟合时，离散数据点的拐点是决定曲线几何形状的重要主导点之一。

图2中，设Ti为向量QiQi+1与QiQi+2的叉积，Ti+1为Qi+1Qi+2与Qi+1Qi+3的叉积，αT为向量 Ti和Ti+1的夹角。离散数据点拐点的计算方法满足：

图2　离散数据点的拐点计算Fig.2　The inflection point of discrete path points

对于平面数据点而言，若Qi+2为曲线的拐点，那么αT的值为π，反之，αT的值为0；如果是空间曲线，对于由CAM系统生成的连续复杂曲线的微小直线段路径点而言，连续4点可近似看作位于同一平面内，所以，若Qi+2为曲线的拐点，则αT为一个较大的值（接近于π），反之，αT为一个较小的值（接近于0）。由此可设定一个正参考值αthre，（如αthre=2/3π），若αT≥ αthre成立，则将Qi+2作为曲线的拐点处理，并标记为主导点。

1.3　长度突变点

实验验证具有C2连续性的局部插值算法的要求之一是，相邻微小直线段间的长度比值必须控制在一定范围内，否则插值生成的曲线会出现扭曲或尖点（图3），这是由算法本身连续性的限制条件造成的。为了解决此矛盾，需通过长度均分策略增加数据主导点，以保证相邻主导点线段之间的长度比值变化较均匀。本文定义了长度突变系数λ=，以及长度突变阈值λ（本实验选取limλlim=3）。在长度均分过程中会出现图4中的两种情况，当线段的长度突变系数λ大于设定阈值λlim时，需要对长线段进行均分处理。

由图4a可以看出，第1段长度（第1个主导点与第2个主导点连线段长度）与第2段长度（第2个主导点与第3个主导点连线段长度）的比值大于λlim，预计将原始数据点下标为istart,new=(istart+imiddle)/2的点设置为新的主导点，并将istart,new的值赋给istart。由于选取数据点下标的中点并不能保证分割后的相邻两线段的长度接近相等，因此需对istart,new的值作进一步调整，以保证QistartQistart,new的长度和Qistart,newQiend的长度比值达到最合理。若istart,new=istart，则令 istart,new=imiddle。

图3　长度不均匀造成的拟合尖角Fig.3　The sharp fitting angle caused by unevenness of the length between points

图4　长度均分策略Fig.4　Length equalization strategy

由图4b可以看出，第2段长度与第1段长度的比值大于λlim，预计将下标为iend,new=(imiddle+iend)/2的点设置为新的主导点，并将iend,new的值赋给iend，同样可通过进一步调整，保证QimiddleQiend,new的长度与Qiend,newQiend的长度比值达到最合理。若iend,new=imiddle成立，则将 imiddle赋值给 istart，否则，istart值不变。

通过不断地循环迭代，可实现主导点间的长度比值达到预设范围之内的要求。由于迭代运算的原因，本文提出的查找主导点方法比较耗时，但是在离线数据预处理阶段完成，并不会对在线拟合阶段的效率造成影响。

2　C2连续的3次Bezier曲线局部插值算法

n次Bezier曲线C(u)的表达式如下：

式中，Pi为曲线控制点；Bi,n为Bernstein基函数。

n次Bezier曲线C(u)的一阶求导公式为

根据式（6）可知，对于两条相连的3次Bezier曲线，公共端点D处的一阶导矢计算公式为

式中，D为相邻两条Bezier曲线C1(u)和C2(u)的连接点；为C1(u)的第3个控制点；为C2(u)的第2个控制点。

为了保证曲线C1(u)和C2(u)在连接点D处一阶连续，联立式（7）、式（8）可得

同理，两条曲线在连接点D处的二阶导矢计算公式为

同理，为了保证两条曲线在连接点D处二阶连续，联立式（10）、式（11）可得

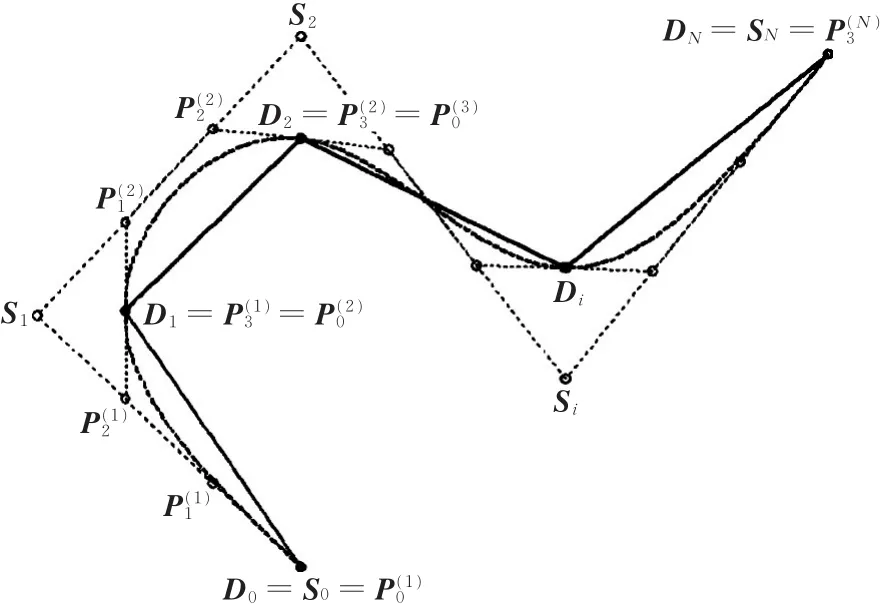
图5　具有C2连续性的Bezier曲线局部插值过程Fig.5　Local Bezier curves interpolation fitting with C2 continuity

根据以上分析，为了保证所有分段Bezier曲线之间的C2连续，以下方程组必须成立：

通过进一步简化，方程组（式（15））可改写为

当i=0和i=N时，令Q0=S0，QN=SN，则式（16）为一线性方程组，可将其改写为矩阵形式。通过矩阵求解得到所有Si后，将其代入式（15），进而可求出所有Bezier曲线段的控制点Pi1和Pi2，且有 P(i)0=Di-1及 P(i)3=Di。

从以上求解Bezier曲线段控制点的过程中可发现，此方法不涉及Bernstein基函数的求解，大大减少了运算量，很适合计算机的快速求解。除了具有控制点求解快速、方便的优点外，Bezier曲线还可同样在不求解Bernstein基函数的情况下，快速计算曲线上对应的参数点。

3　Bezier曲线拟合后的非主导点误差检测与轮廓误差跟随法

3.1　de Castejau算法简述

本文提出的在数据预处理阶段对主导点进行具有C2连续性的插值拟合算法的另一个优点就是，在非主导点的误差检测过程中可充分利用de Castejau算法求解曲线及其导数曲线上的参数点，以提高非主导点误差的计算速度。由于de Castejau算法是一种线性插值算法，在数值计算时受计算机浮点舍入误差影响较小，因此也有利于提高计算精度。此外，由Bezier曲线的一阶求导公式（式（6））可知，其导数曲线也是一条Bezier曲线，所以曲线及其导曲线上点的求取可利用同一套算法，从而精简了程序的代码量。

当n=3时，3次Bezier曲线上参数点的求解展开式如下：

由式（17）可知u=0.5时的de Castejau计算过程（图6）。

3.2　Bezier曲线拟合后的非主导点误差计算

点到参数曲线的误差计算通常使用牛顿迭代法，且误差定义如下：

牛顿迭代法的初始值u，可通过对Bezier曲线段内非主导数据点进行弦长参数化［9］求出。计算第i段Bezier曲线内所有非主导点到曲线的距离误差，并将超过设定阈值的误差最大点设为新的主导点（图7）；重新利用长度均分策略计算长度均分点，并再次将Bezier曲线拟合后计算出的非主导点中误差超限且最大的点作为新的主导点，如此循环，直到所有非主导点的误差达到预处理阶段拟合误差允许值的范围内。

图6　de Castejau算法线性插值过程Fig.6　de Castejau linear interpolation process

图7　非主导点误差计算与新增主导点Fig.7　Non-dominant points error calculation and new added dominant point

3.3　轮廓误差跟随法计算B样条拟合误差

对主导点进行插值拟合生成B样条曲线后，需对非主导点的拟合误差进行检测。由于此过程需要在线完成，而传统牛顿迭代法的误差计算时间较长，算法效率较低，因此为提高算法的效率和减少误差计算时间，本文利用文献［15］中提出的轮廓误差跟随检测方法，计算非主导点到拟合曲线的误差。实验结果表明：相比牛顿迭代法，轮廓误差跟随法对同样数量点到复杂曲线的误差检测时间更短，且其计算所需的曲率值可提前算出，并用于后续B样条曲线插补速度规划预处理时速度突变点的检测，从而提高了算法的效率。

图8中，C(ui)为非主导点Qi在曲线上的估算投影点，C(ui+δ)为非主导点Qi在曲线上的实际投影点，δ为Qi对应的ui估算误差，e(Qi)为非主导点到曲线的实际误差。根据文献［15］，e(Qi)的二阶泰勒展开表达式为

式中，K为B样条曲线在C(ui)处的曲率；dt为矢量D在矢量T上的投影长度，o3(dt)表示截断误差；dc为矢量D在矢量C上的投影长度；T为曲线在C(ui)处的切向矢量；N为曲线在C(ui)处的单位主法矢量；C为D在C(ui)处主平面上的投影，且T、N、C均为单位向量。

图8　误差跟随法计算B样条拟合误差Fig.8　B-spline fitting error calculation by error following method

由图8可知，为了提高误差跟随法的误差检测精度，必须合理估算非主导点Qi对应的参数值ui。通常，对主导点进行B样条插值拟合时，其节点向量是通过对主导点进行弦长参数化得到，而非主导点的参数值可通过再次对两主导点间的数据进行弦长参数化得到。为了统一节点向量和数据点对应参数值的计算方法，本文采用原始数据，对主导点进行B样条拟合时的节点向量进行合理规划。设主导点Dj在原始数据点中的下标存储在数组mark[N]中，其中N为原始数据点的个数，则进行B样条拟合时，主导点处的参数值计算方法如下：

4　算法流程与仿真分析

4.1　算法流程

为了验证本文所提方法及算法的正确性，以Visual Studio 2008为平台，编写了主导点（数据预处理）选取、主导点B样条插值拟合及非主导点误差计算的C++源程序，其算法流程见图9。其中，数据预处理阶段的误差检测容差e1设置较大，本文取e1=0.1 mm；实时处理阶段的误差结果一定小于e1，其检测容差e2直接设置为最终的拟合误差，本文取e2=0.03 mm，且在线处理时只需1次误差检测循环，并将超过误差的非主导点增加为新的主导点，对更新后的主导点再次进行插值拟合生成B样条曲线，此时的拟合误差一定在e2范围内。

图9　算法流程图Fig.9　Algorithm flowchart图12　主导点B样条插值拟合Fig.12　Dominant points and B-spline curve

4.2　仿真分析

本文的仿真案例为1条连续的半蝴蝶状曲线，通过UG NX8.0软件生成加工路径，离散点内外公差绝对值均设置为0.02 mm。通过数据预处理后，筛选出138个主导点，原始数据点和主导点的分布见图10。

图10　主导点的组成部分Fig.10　Components of dominant points

主导点主要由离散数据点的曲率极大值点、曲率阈值点、曲线拐点、长度突变点以及误差超限点组成。由图10中的3处尖角放大图可知，通过比较当前曲率值点与前后5个连续相邻曲率值点确定曲率极大值点，能很好地消除数据波动造成的伪曲率极大值点，但会漏选曲率阈值点处的曲率极大值点（图11），不过，这些点已通过曲率阈值点进行补选。对于除去特殊形状标记覆盖的叉形标记主导点，其生成方法是，对非主导点进行长度均分策略处理，将长度突变点记为主导点，以及将Bezier曲线拟合后的误差超限点补选为主导点，此过程通过迭代计算完成，且每次迭代循环时都要重新进行长度均分处理及Bezier曲线拟合。

图11　2点与5点比较法生成的曲率极大值点Fig.11　Local curvature max points with 2 and 5 points method

对主导点进行B样条插值拟合后生成的曲线见图12。

图9　算法流程图Fig.9　Algorithm flowchart图12　主导点B样条插值拟合Fig.12　Dominant points and B-spline curve

将主导点插值拟合成B样条曲线后，需要对非主导点进行误差检测，本文采用误差跟随法计算拟合误差，以保证此过程的快速和高效性，并将其结果与牛顿迭代法的计算值相比较。结果表明：两种方法的方法误差小于0.01 mm。图13为两种计算方法的误差计算值对比图。

图13　两种方法的误差计算值对比图Fig.13　Comparison of error calculation values of the two methods

测试结果表明：对133个非主导点进行误差计算，通过牛顿迭代法（其距离检测精度为0.001 mm）需要循环计算275次，共耗时8.6 ms；而误差跟随法只需要循环计算133次，共耗时5.537 ms，误差跟随法节省时间约35.6%。对138个主导点进行1次B样条插值拟合的时间为647.435 ms。由于在线处理最多只需进行2次B样条插值拟合，因此，相比传统的插值拟合方法，在允许时间内，误差跟随法可一次性在线拟合更多的数据点，从而提高了拟合效率。

5　结论

（1）通过仿真实验可知，本文提出的基于主导点的B样条插值拟合方法可实现对复杂数控加工刀具轨迹（即G01代码）的平滑压缩，且利用轮廓跟随误差法的二阶泰勒展开式计算拟合误差，可在允许的误差范围内提高计算效率。

（2）由于所提方法的数据预处理过程可在离线阶段完成，而在线处理阶段只包含1次误差检测循环和最多2次B样条插值拟合，因此根据数控系统的处理能力，若合理调整处理的数据量，此方法可实现刀具轨迹的在线甚至实时平滑压缩计算。

（3）为了验证理论的正确性，本文选取了形状较复杂的半蝴蝶状曲线作为仿真实例，实验证明，将原始的271个离散数据点压缩成以B样条曲线控制点形式存储的138个数据点，其压缩效率可提高近2倍。若曲线形状不复杂，可在数据预处理阶段适当增大长度突变阈值，从而减少主导点数量，其压缩效率将会进一步提高。