学生接受假设的认知困难与课程及教学对策

何小亚，李湖南，罗 静



学生接受假设的认知困难与课程及教学对策

何小亚1，李湖南1，罗 静1，2

（1．华南师范大学 数学科学学院，广东 广州 510631；2．韶关学院 数学与统计学院，广东 韶关 512005）

运用质性研究方法揭示了学生在数学概念、原理和证明的认知过程中接受假设的认知困难，并就数学教学和教材编写提出了解决问题的对策．学生面临的认知困难主要表现在：难以接受抽象的定义和公理化的数学原理；难以接受数学定义、原理和证明中的假设条件；学生证明了一个命题与相信该命题是两回事．克服接受假设的认知困难的对策：一是分别按照概念形成的教学模式和由例子到原理的教学模式来教抽象的数学定义和数学原理；二是按照数学概念、数学原理发展的历史来设计教学；三是数学证明的理解与接受离不开实用性证明的帮助；四是教材的编写要尽量降低学生接受假设的门槛，否则教师要为学生搭建理解的“脚手架”．文科生和理科生都可以学习曲线与方程、数学归纳法的内容．

接受假设；认知困难；数学学习；教学；课程；对策

1 引言

在国外，很多人对数学的评价是：“我憎恨数学！它简直无法理解，我也没办法教别人学数学！”“我数学很糟糕，数学一直是我最讨厌的学科．”“我痛恨课堂上的数学……我从来没有改变过对数学的厌恶感．”[1]在国内，“大众不喜欢数学”这一现象更是十分普遍[2]．要解决“大众不喜欢数学”的问题，数学教育必须以理解为价值取向，追求数学素养的达成．文[3]指出：数学素养是指满足学生自身发展和社会发展所必备的数学方面的品格和能力，是数学的知识、能力和情感态度价值观的综合体现；数学素养可以由低到高分成数学知识和技能、数学过程和方法、数学情感态度价值观这3个层次．

过程与方法目标，尤其是情感态度价值观目标的缺失是导致“大众不喜欢数学”这一现象最直接的原因．另外的原因，可能与学生在数学概念的建构、数学原理的获得和数学证明的认知过程中接受假设的认知困难有关．

所谓接受假设，是一种在心里接受一个数学概念或原理的陈述，并予以使用，而不必关注其合理性的数学思维方式．学生往往因为不接受某一个数学概念或原理中的前提条件（或称假设条件）而导致不接受这个数学概念和原理．

文[4]指出：“数学核心素养是指满足学生终身发展和社会发展所必备的、关键的数学素养．其包括：数学化、数学运算、数学推理、数学意识、数学思想和数学情感态度价值观．数学化包括形式化、图式化、数学建模．”之所以没把公理化列为数学化这一核心素养的内容的原因，一是公理化的目标是从少数不加定义的原始概念和不加证明的公理出发，运用逻辑推理规则把一门学科建立成为演绎系统，这主要是数学工作者的任务；二是考虑到了学生接受假设的认知困难．

那么，学生在数学学习中存在着哪些接受假设的认知困难，如何帮助学生克服这些困难？为此，结合中学数学课程中的样例，运用质性分析方法分别讨论数学概念、数学原理和数学证明中与接受假设有关的学习、教学、教材诸方面的问题，并就教学和课程处理提出相应的对策．

2 研究结果

2.1 数学概念的建构

在数学概念的建构过程中，学生接受假设的认知困难表现在：一是难以接受抽象的定义；二是难以接受定义中的假设条件．

2.1.1 难以接受抽象的定义

众所周知，数学科学具有高度的概括性、逻辑的严谨性和应用的广泛性．有许多抽象的数学定义，在经历了漫长的历史发展过程后，最终以最精确、最概括的科学性定义方式呈现，这对学生的理解造成了困难．

例如，极限的精确定义是学生理解的一个难点，他们在心理上难以接受定义这一假设．教材[5]遵照极限概念发展的历史进程引入这一概念，较好地解决了这一难点．即：先由样例概括出极限的直观定义，再用此定义解决一些极限问题，最后给出极限的符号形式．但可能是由于教师教学的问题，学生难以真正理解极限概念．这批学生进入大学后，大学教授对“煮夹生饭”式的讲极限十分不满．于是，2003年实施的高中数学新课程去掉了极限的定义，但在讲导数定义时，依然使用了极限这一符号．针对这一尴尬的处理，文[6]解决了“不学极限定义也可以学习导数！”这一问题．

再如，由于学生难以接受抽象的“曲线与方程”概念和教师教学的困难，高中数学新课程将其内容放到选修2-1中供理科生学习，而文科生则不学此内容．尽管课程标准要求不讲曲线与方程的概念，但难能可贵的是教材[7]在直线方程部分以探究思考方式，在圆的标准方程部分以证明的方式保证了纯粹性与完备性．但许多一线教师却无法有效地解除学生的困惑：圆的方程已经求出来了，为什么还要多此一举地说明：若点的坐标适合圆的方程，则该点在此圆上．这就是缺少“曲线与方程”这个证明依据的尴尬．

数学本来是最讲道理的，不能因为教师没有讲好抽象的曲线与方程概念而妥协．为此建议新教材必须向师生清楚地回答以下3个问题．

问题1：为什么要求直线、圆等曲线的方程？

问题2：求曲线的方程实质上就是求什么？

问题3：需要满足什么条件，一条曲线和一个方程才能互为彼此？

问题1的处理思路：简单有趣的实际问题→水平数学化→几何曲线问题→代数化→方程问题→方程求解→解释答案→得到实际问题的答案．

问题2的处理思路：求曲线的方程实质上就是求该曲线上任意一点的坐标所满足的关系式！为此需要建立直角坐标系，设点坐标，抓住该曲线上的点满足的几何性质，将此几何性质代数化得出方程，证明这个方程就是所求的曲线方程．

问题3的处理思路：直线方程采用教材[7]的处理，在圆的标准方程之前一节加入曲线与方程的内容，通过直线、射线、线段这3类简单的曲线与其对应的方程及其反例来回答：需要满足什么条件，一条曲线和一个方程才能互为彼此？

如何解决学生难以理解科学数学定义这一问题，苏联数学家阿·尼·柯莫戈洛夫（1903—1987）指出：“数学不能从定义开始．去定义一些概念，我们就不可避免地要在这些定义中应用一些其他的概念．当我们不理解一些概念的含义时，我们就不能前进一步，不能表述出任何一个定义．因此，任何一个数学理论的叙述要从一些不用定义的概念开始．用它们就已经可能去表述深入一步的任意的概念．人们如何互相解释自己对基础概念的理解呢？对于这一点没有其他方法，只有在例子中借助于对确定事物典型性质的详细描述来阐明．这些描述可以在细节上不完全清楚并且可以不彻底．但是具有足够清晰程度的概念的内涵就可以逐渐从它们中显示出来．”[8]

事实上，如何解决学生难以接受抽象的科学数学定义这一问题，张景中院士另辟蹊径，提出了“改造数学使之更适宜于教学和学习”的教育数学理念[9]．教育数学就是为了帮助学生理解科学数学而改造的数学．张景中院士在大学微积分教学和中学几何教学实施了“重建微积分”“重建平面几何”和“重建三角”的改革试验，取得了较好的成果[10-15]．

2.1.2 难以接受定义中的假设条件

学生对高中的古典概型和几何概型概念的理解存在着普遍的认知困难，主要原因是师生没有真正理解随机事件这一核心概念，这与教材的定义有关．

教材[16]不讲随机试验，只通过掷硬币和掷骰子试验的结果，以揭示外延的方式定义了基本事件．而教材[17]定义为：“在一次试验中可能出现的每一个基本结果称为基本事件（elementary event）．”满足以下条件的随机试验的概率模型称为古典概型（classical probability model）：①所有的基本事件只有有限个；②每个基本事件的发生都是等可能的．这些定义没有说明清楚“一次试验”和“随机试验”是什么？

对于几何概型，学生难以接受教材中定义的假设：“如果事件发生的概率只与构成该事件区域的测度成比例．”

由于学生心理上无法接受这些定义及其假设，自然会产生理解上的困难，出现了负面的学习态度．

为此，文[18]提出了新的高中数学教材编写及教学思路理论框架，以及重构高中概率教材的方案．

A. 介绍确定性现象、随机现象、概率论的发展简史（可放入本章概览）．

B. 引入随机试验的概念，由此给出基本事件、样本空间、随机事件的概念．

C. 通过实例介绍随机事件的包含、相等、并、交、对立、互斥等关系．

D. 先介绍概率的概念，再介绍通过随机试验，用频率去估计概率．

E. 先指出用频率去估计概率的局限性，再介绍特殊的、理想化的古典概型可以克服用频率去估计概率的局限性．

F. 讨论概率的基本性质．

G. 先指出古典概型的局限性，再讲更特殊、更理想化的几何概型，最后讲随机模拟试验．

并指出，概率论是研究随机现象的科学，随机现象是通过随机试验来研究的．概率是反映随机事件发生的可能性大小的数值，人们常常用它来研究刻画随机现象．随机事件由随机试验来确定．导致学生和教师错误理解概率问题的根本原因是：现有的许多教材将随机现象与随机事件混为一谈，不讲随机试验就来讲随机事件，用随机现象来定义随机事件，完全没有理解好、处理好真实世界与数学世界的关系．

2.2 数学原理的获得

在数学原理的获得过程中，学生接受假设的认知困难表现在：一是喜欢刨根问底的学生对公理化的数学原理的困惑；二是难以接受数学原理中的假设条件．

2.2.1 喜欢刨根问底的学生对公理化的数学原理的困惑

中学数学教材中有许多诸如有理数乘法的符号法则、祖暅原理、线面平行的判定定理等数学原理，由于学生认知基础的缺乏和证明本身的抽象性，教材采取了公理化的处理方式．这对于能接受假设的学生而言，不存在认知上的困难，但对于喜欢刨根问底的学生而言，则会产生许多困惑．

例如，在学习有理数的运算法则时，如果学生心理上不接受“负负得正”这一公理化的数学原理，而教师又不解决学生接受假设这一认知困难，那么学生就会形成消极的情感态度价值观．

2001年获得中国国家科技最高奖的“杂交稻之父”袁隆平院士在接受CCTV记者采访时说过：“我最喜欢外语、地理、化学，最不喜欢数学，因为在学正负数的时候，我搞不清为什么负负相乘得正，就去问老师，老师说你记得就是；学几何时，对一个定理有疑义，去问，还是一样回答，我由此得出结论，数学不讲道理，于是不再理会，对数学兴趣不大，成绩不好．”[19]

为了解决像袁隆平院士这样喜欢刨根问底的学生接受“负负得正”这一假设的认知困难，易倩善、罗静和陈绮云提供了两种不同的教法[19]．

解除学生对公理化的数学原理的困惑是教材编者和数学教师的责任．作为教材编者，对公理化的数学原理要尽量为读者提供有说服力的“理由”，而作为教师，则必须随时准备好面对学生的质疑，以解除其心中的疑虑．

2.2.2 难以接受数学原理中的假设条件

数学归纳法是一种独特的数学原理，由于中学教材中没有皮亚诺公理或最小数原理作前提，这就使其教学缺乏认知基础，变成无“法”可依．数学归纳法的工具性理解（Instrumental Understanding）问题不大，但其关系性理解（Relational Understanding）却十分困难，成了一个世界性的教学难题．中外研究[20-22]表明，学生理解数学归纳法最大的困难是：不理解“假设结论成立，然后再去证明结论成立”，也就是说，“()不是作为被证的事实，而是作为假设；对蕴涵关系→的不理解”．

为克服这一困难，教学的定位应该是：既要教操作步骤，更要教原理的理解；既要提供“公理”的背景，更要借助日常情境模型把重点放在对蕴涵关系→的理解上．蕴涵关系（Implication Relation）实质上是公理，没办法讲清楚，唯一可行的方式是将抽象具体化，即找一个有蕴含关系的具体模型，以帮助学生突破理解的困难．

具体作法是通过“摆好的”多米诺骨牌来搭建理解的“脚手架”．所谓“摆好的”多米诺骨牌就是这些骨牌之间有这样的关系R：“假设第块倒下，那么第+1块一定倒下．”为此需要做两件事：

（1）通过一些没摆好的骨牌作为反例来强化什么叫做摆好；

（2）通过“摆好的”多米诺骨牌，说明这一关系R与第块倒没倒下没有关系．

最终，由此模型类比理解：递推关系就好比是多米诺骨牌间存在的关系R：“假设第块倒下，那么第+1块一定倒下．”“假设时结论成立”相当于“假设第块倒下”．因为骨牌间的关系R是与第块倒没倒下没有关系的，所以递推关系是与“假设结论成不成立”没有关系的[23]．

2.3 数学证明的学习

在数学证明的学习过程中，学生接受假设的认知困难表现在：一是学生证明了一个命题与相信该命题是两回事；二是不接受数学证明中的假设条件．

2.3.1 学生证明了一个数学命题与相信该命题是两回事

Bell（1978）将证明分为实用性证明与理性证明．实用性证明以个人的经验、权威的认可、观察到的实例、举不出反例、结论的有效性作为依据，它依赖于事实．而理性证明则以逻辑推理论证为依据，它是思想实验，不依赖事实．数学证明就是一种理性证明，它可用一个反例来反驳[24]．

数学家不认可实用性证明，只接受数学证明．对于不少学生而言，尽管他们已经形式地、逻辑地证明了一个数学命题，但并不完全相信该命题．

例如，许多高中生用数学归纳法证明了一个恒等式后，仍然将=3, 4, 5代入恒等式验算后才解除了心中的怀疑．

Fischbein和Kedem（1982）在一份问卷中给出命题“是四边形，、、、依次为各边的中点，则四边形是平行四边形”的证明后，问学生是否承认结论在所有情况下成立，并提出以下问题：“某人对此有怀疑，他认为我们还需要至少检验100个这样的图形，才能确信四边形是平行四边形．你的看法是什么？请你做出解释．”在相当于高一至高三学生答卷中，认为完全不必再做检验者不超过10%，而约有三分之一的被试既承认证明是普遍有效的，但又不反对另外再做检验[24]．这一调查结果说明：证明不保证相信．

数学证明的理解与接受需要实用性证明的帮助，这是以理解为价值取向的数学教育的需要．Bourbaki学派认为，每个数学工作者都知道，单是验证了一个数学证明的逐步逻辑推导，却没有试图洞察获取这一连串推导的背后意念，并不算理解了那个数学证明[25]．

2.3.2 不接受数学证明中的假设条件

数学本质上是从一些定义、公理、公设出发，按照逻辑推理规则得出的一套演绎系统．要证明命题P1成立，需要命题P2成立，…，需要命题P成立，如此追溯下去，数学证明的可靠性最终回到定义、公理、公设的可靠性，但遗憾的是定义、公理、公设的可靠性无法再继续证明．

追根溯源，代数系统的产生源自于数1，1生2，2生3，3生万物（算术、字母表述数、代数式、函数、函数空间、算子，……）；几何系统最基本的元素是点，点动成线，线动成面，面动成体．而1是单点集合的标志，点是能标明位置但却没有大小范围的东西．它俩在真实世界里是不存在的，于是由它俩演绎出来的代数和几何是不存在的．也就是说，从真实世界的角度看，数学是不存在的，是虚的，看不见，摸不着．

数学没有声音，无法让人感觉到旋律和节奏；数学没有色彩，无法让人欣赏到绚丽和斑斓；数学没有肌肉和神经，无法让人感受到伤痛和肌肤之亲；数学没有自然科学的试验，无法让人看到神奇的物质运动变化；数学语言没有母语所表示的鲜活生灵，无法让人重构人间的悲欢离合．数学世界是人类心智的构造，是思维存在，是无法证实的．因此，接受数学证明链条上的命题P和定义、公理、公设的可靠性，成了学生认知的困难．

例如，教材[7]利用祖暅原理来推导柱体的体积等于底面积乘以高时，需要接受3个假设：一是祖暅原理；二是对于任意一个底面积为的柱体，可以作出一个面积是的矩形；三是长方体的体积等于底面积乘以高．只要学生对某一假设不接受，就无法顺利进行后续的推理．

祖暅原理的发现源自于公元6世纪数学家祖冲之的儿子祖暅的直觉，因为其严谨的逻辑证明需要以微积分理论为基础．在中学只能借助实物模型，利用特殊到一般的思维方式，引导学生接受这一假设．

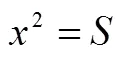
利用小学建立起的长方体的体积公式经验，学生接受假设三没有问题，但教师要准备好回答“为什么长方体的体积等于底面积乘以高？”如果没有深刻理解度量的本质，很多教师是回答不清楚这一问题的．

数学证明是经得起数学家拷问的演绎推理证明．数学证明的价值不仅仅是获得数学形式演绎推理的结构和细节，其更大的教育价值表现在：（1）理解、深化数学概念；（2）巩固、掌握数学原理；（3）获得数学证明的思维方式：由因导果，执果索因，上下紧逼，前后夹攻，思路贯通——找到了题设和结论的逻辑联系；（4）训练提高数学推理能力，培养理性精神和创新能力；（5）学会逻辑地表达交流；（6）理解命题，相信数学结论，获得数学自信．

学生在数学证明学习的认知过程中，接受假设的认知困难会对上述6条教育目标的实现产生消极作用．

3 问题的讨论

3.1 “重建三角”中的假设问题

尽管“重建三角”是一项极具创新的改革，也取得了很好的效果[15]，但要学生很好地接受这一新体系，还需要解决学生接受假设这一难点．

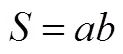
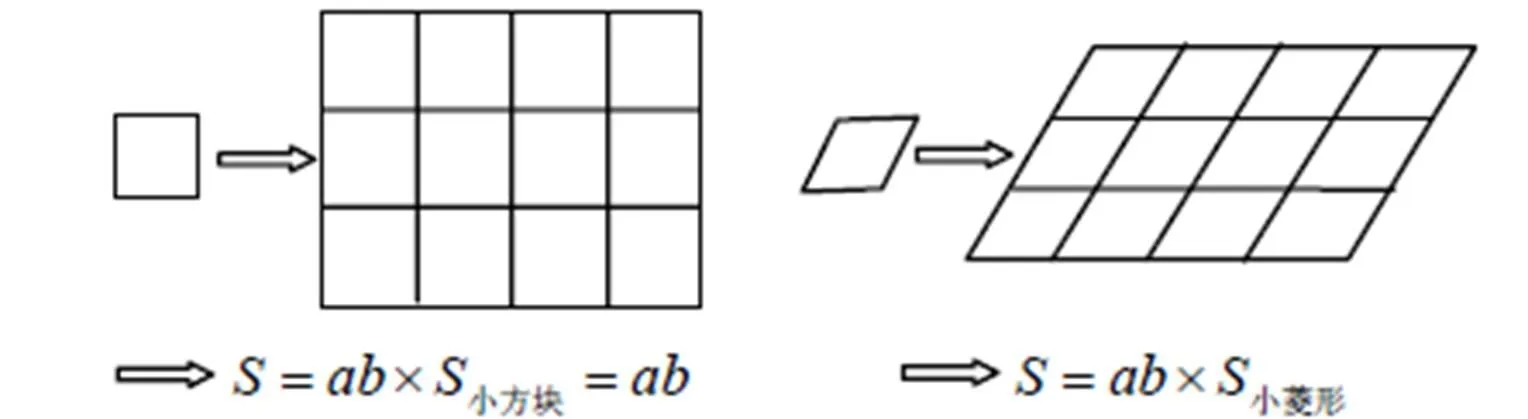
可以考虑这样的处理方案．

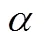
（1）若、都是有理数，只要度量单位足够小，可以恰好量出、都是正整数；

（2）若、中有无理数，根据实数的Cantor构造，无理数是一个有理数基本序列的极限，无限地运用（1）的方法，就可以把无理数“量出”整数．

显然，解释（2）是难以被人接受的，教师可以告诉中学生，等你读了大学就能理解（2）的解释．可笑的是，所使用的数学分析教材是不讲实数的构造理论的，很多大学生也搞不清楚“为什么长方形的面积等于长乘以宽？”

3.2 弧度制中的接受假设问题

解决引入弧度制的必要性与合理性问题，一条思路是按照弧度制发展的历史设计教学[26]；另一种方法是借用汽车里程表模型来说明弧度制的必要性与合理性．

4 结论与展望

4.1 研究结论

研究结果表明，在数学概念、数学原理和数学证明的认知过程中，学生接受假设的认知困难主要表现在：一是难以接受抽象的定义和公理化的数学原理；二是难以接受数学定义、数学原理、数学证明中的假设条件；三是学生证明了一个命题与相信该命题是两回事．克服学生接受假设的认知困难的对策，一是尽量按照概念形成的教学模式和由例子到原理的教学模式[27]来教抽象的数学定义和数学原理；二是按照数学概念、数学原理发展的历史来设计教学[28-31]；三是数学证明的理解与接受离不开实用性证明的帮助；四是教材的编写要尽量降低学生接受假设的门槛，否则教师要为学生搭建理解的“脚手架”，以利于学生克服接受假设的认知困难；五是加强运用教育数学的理念来重构部分中学数学的改革实验．

接受假设，甚至是不理解地接受假设，是数学认知的助推器．无法接受假设会造成学生的思维受阻，数学认知无法继续．无法接受假设的经验增多，会导致“数学就是规定”“数学就是符号游戏”“数学索然无味”这些不良的数学情感态度价值观．没有理解，就有了“伤害”．追求理解、追求数学核心素养的达成自然就成了数学教育的必由之路，这一目标的实现要靠数学课堂三维目标的设计[32]、实施、反思来完成．

不理解地接受假设，尽管不影响认知的继续，但却影响了数学素养的达成．例如，中国学生从小学开始一直到大学，对分数除法十分熟练，但却无法解释“为什么除以一个分数等于乘以其倒数？”也无法画图予以说明为什么，更无法独立发现这一数学原理．在旧的课程体系之下，中国学生的理解水平处于工具性理解层次，无法达到关系性理解层次．也就是说，尽管学生习得了一些智慧技能，但无法理解其合理性和必要性，达不到数学素养要求的层次．

4.2 几点建议

（1）研究结果表明，不讲曲线与方程的概念就来讲圆的标准方程，出现了逻辑上的尴尬，这是喜欢质疑的学生无法接受的．只要解决了曲线与方程的教学问题，文科生和理科生均可以学习曲线与方程的内容．

（2）在中国，2003年的高中数学课程标准将数学归纳法安排在数学选修2-2中，但这一模块要学习导数及其应用（24学时）、推理与证明（8学时）、数系的扩充与复数的引入（4学时），而数学归纳法被放在“推理与证明”模块中．由于课程标准只要求达到“了解”层次，加上高考主要以导数及其应用为重头戏，许多省份很少考数学归纳法（广东省除外），导致许多学校不讲数学归纳法，造成进入大学学习的这些考生的基础缺失．

研究结果表明，学生学习数学归纳法最大的困难是由难以接受假设造成的．只要解决了数学归纳法的教学问题，文科生和理科生均可以学习数学归纳法．

学习数学归纳法，最有价值、最精彩的就是要学习一种思维方式，也就是说，要先从个别样例中的观察、思考中去探索规律，再从一般性上来进行逻辑证明，实现由简到繁，由有限到无穷的突破．但中国的高中课程标准把数学归纳法的学习要求仅仅列为“了解”层次，造成了舍本求末的现状．建议在新修订的高中数学课程标准中将其调整为“理解”层次．

（3）中学概率学与教中存在的问题与教材的处理密切相关，更深层次的原因是学生难以接受假设，解决这些问题的唯一途径是需要重构概率模型的课程体系．这与章建跃和程海奎（2017）的研究结果[33]是一致的．

4.3 研究展望

这项质性研究只是结合一些案例指出了学生在数学概念学习、数学原理获得和数学证明的认知过程中接受假设的认知困难的类型，还缺少定量的实证研究．以下类型的问题值得研究者继续研究：

小学、初中、高中和大学的数学学习中还存在着哪些接受假设的认知困难？

接受假设对某一数学概念、原理、证明的学习有什么影响？（调查、实验研究）

接受假设对数学问题解决有什么样的影响？

致谢：感谢天津师范大学教师教育学院王光明教授为文章提供了建设性的意见．

[1] HERSH R，STEINER V J．爱+恨数学[M]．杨昔阳，译．北京：商务印书馆，2013：336．

[2] 何小亚．2016年数学高考全国Ⅰ卷的认知分析和备考及命题建议[J]．中学数学研究（上半月），2016（10）：封二-10．

[3] 何小亚．学生数学素养指标的理论分析[J]．数学教育学报，2015，24（1）：13-20．

[4] 何小亚．数学核心素养指标之反思[J]．中学数学研究（上半月），2016（7）：封二-4．

[5] 人民教育出版社中学数学室．全日制普通高级中学教科书（实验修订本）数学第三册（选修Ⅱ）[M]．北京：人民教育出版社，2004：75-77．

[6] 何小亚．高中数学新课程微积分的课程设计分析[J]．数学通报，2006，45（4）：9-13．

[7] 人民教育出版社．普通高中数学课程标准实验教科书数学2（必修，A版）[M]．北京：人民教育出版社，2001：124-125．

[8] 阿·尼·柯莫戈洛夫．函数是什么[J]．姚芳，译．数学教学，2001（3）：27-30．

[9] 张景中．教育数学探索[M]．成都：四川教育出版社，1994：12-15．

[10] 张景中，陈文立．非-极限理论与微积分的教学改革[J]．大学数学，2004，20（5）：1-4．

[11] 张景中．几何新方法和新体系[M]．北京：科学出版社，2009：整体引用．

[12] 张景中．重建三角，全局皆活——初中数学课程结构性改革的一个建议[J]．数学教学，2006（10）：封二-4．

[13] 李苹芳，朱华伟．初等数学新体系的教学实验调查与分析[J]．数学教育学报，2015，24（2）：26-29．

[14] 朱华伟，徐章涛．教育数学：缘起、旨趣、现状和意蕴[J]．数学教育学报，2015，24（3）：30-32．

[15] 张景中．把数学变得更容易[J]．新课程评论，2016（5）：7-13．

[16] 人民教育出版社．普通高中数学课程标准实验教科书数学3（必修，A版）[M]．北京：人民教育出版社，2007：125-136．

[17] 单墫．普通高中数学课程标准实验教科书数学3（必修系列）[M]．南京：江苏教育出版社，2005：90-107．

[18] 何小亚．高中概率模型学与教中的问题和对策[J]．数学教育学报，2017，26（1）：37-40．

[19] 何小亚．中学数学教学案例精选[M]．北京：科学出版社，2011：3-14．

[20] 菲施拜因．理解数学归纳法原理的心理困难．（转引自：张奠宙．数学教育研究导引[M]．南京：江苏教育出版社，1994：399-404．）

[21] 季建平．关于理解数学归纳法原理的心理困难的实验报告[J]．数学教学，1998（3）：33-35．

[22] 李丹艳．关于“数学归纳法”的调查报告[J]．数学教学，1999（3）：14-15．

[23] 詹欣豪，何小亚．数学归纳法教学的困难、对策与价值[J]．中学数学杂志，2014（9）：6-9．

[24] 李士锜．PME：数学教育心理[M]．上海：华东师范大学出版社，2001：129，132．

[25]  BOURBAKI．数学的建筑[M]．胡作玄，译．大连：大连理工大学出版社，2014：整体引用．

[26] 江灼豪，何小亚．弧度制发展的历史溯源[J]．数学通报，2016，55（7）：14-17．

[27] 何小亚．数学学与教的心理学[M]．2版．广州：华南理工大学出版社，2016：171-183．

[28] 张晓明，汪晓勤．中学数学教学中融入数学史的行动研究[J]．数学教育学报，2009，18（4）：89-92．

[29] 徐章涛，梅全雄．HPM视角下的数学教材编写[J]．数学教育学报，2009，18（3）：14-17．

[30] 汪晓勤，韩祥临．中学数学中的数学史[M]．北京：科学出版社，2002：整体引用．

[31] 汪晓勤．HPM：数学史与数学教育[M]．北京：科学出版社，2017：整体引用．

[32] 何小亚，姚静．中学数学教学设计[M]．北京：科学出版社，2012：20-24．

[33] 章建跃，程海奎．高中必修课程中概率的教材设计和教学思考——兼谈“数学核心素养如何落地”[J]．课程·教材·教法，2017，37（5）：27-33．

Cognitive Difficulties of Students’ Accepting Assumption and the Strategies of Curriculum and Teaching

HE Xiao-ya1, LI Hu-nan1, LUO Jing1, 2

(1. School of Mathematical Sciences, South China Normal University, Guangdong Guangzhou 510631, China; 2. School of Mathematics and Statistics, Shaoguan University, Guangdong Shaoguan 512005, China)

Using qualitative methods to reveal the cognitive difficulties of students’ accepting assumption in the cognitive process of mathematical concepts, principles and proof, and put forward the countermeasures to solve the problems in the teaching of mathematics and the compiling of teaching materials. Students faced cognitive difficulties in: first, it was hard to accept abstract definition and axiomatic mathematical principles; second, it was hard to accept prerequisites in mathematical definition, principles and proof; third, there were differences between proving a statement and believing one. Solutions for the students’ cognitive difficulties in accepting assumption: first, teaching abstract mathematical definitions and principles in the way of the teaching model of concept formation and the teaching model from examples to principles respectively; second, designing teaching process in the way of the development of mathematical concepts and principles; third, combining with the practical proof; forth, the compilation of teaching materials should try to reduce the threshold for students to accept the assumption, otherwise, the teacher should build an understanding scaffold for the students. Liberal arts students and science students could learn the contents of curves and equations and mathematical induction.

accepting assumption; cognitive difficulties; mathematics learning; teaching; curriculum; countermeasures

[责任编校：周学智]

2018–04–03

广东省高水平大学建设本科生拔尖创新人才培养项目（113-S80712）

何小亚（1964—），男，贵州荔波人，教授，主要从事数学教学与数学学习心理研究．

G420

A

1004–9894（2018）04–0025–06

何小亚，李湖南，罗静．学生接受假设的认知困难与课程及教学对策[J]．数学教育学报，2018，27（4）：25-30．