从历史发展的视角看中学概率教学

张蜀青，曹广福，罗荔龄



从历史发展的视角看中学概率教学

张蜀青1，曹广福2，罗荔龄2

（1．广州市执信中学，广东 广州 510095；2．广州大学 数学与信息科学学院，广东 广州 510006）

按照历史发展的脉络，从古典概型到统计意义下的概率，再到公理化的概率论，对概率论的发展做了简明扼要的阐述，方便一线教师对概率论基本历史有一个初步的了解．同时，通过一系列问题情境的创设，针对中学一线课堂中随机事件、样本空间、古典概型与几何概型等概念的教学提出了具有可操作性的建议．概率教学应遵循几个基本原则：（1）适应学生的认知水平；（2）在尊重历史的基础上改进教学内容；（3）杜绝伪情境．概念的定义应该准确，不同概念之间（基本事件、样本空间、随机事件等）的逻辑关系应该清晰明了．中学阶段不宜设计一些类似贝特朗问题的陷阱，这些问题除了增加学生对几何概型理解的困难，并不能为学生学习概率带来更多的帮助．

随机事件；样本空间；几何概型；古典概型；随机变量

1 引言

概率是中学数学的重要组成部分，也是中学数学教学中的难点，之所以难，主要原因或许来自两个方面：一是很多中学教师对概率论了解不多，有些甚至没有学过概率论；二是一些教材对概念的阐述不够清晰，导致理解上的困难．中学教材首先从频率的角度定义概率，将概率定义为重复随机试验中频率的极限，然后回到古典概型．统计意义下的概率定义是存在逻辑问题的，而且，中学阶段虽然学习微积分，但并不介绍极限概念，教学过程中也很难实现从频率到概率的极限过度，一些教师通过抛硬币或计算机模拟的方法引入概率概念，但显得很不自然，而且任何有限次重复试验的频率与概率都可能相去甚远．所以概率的教学是个值得好好研究的课题．

2 概率论简史

在研究教法之前，首先需要了解一下概率论的前世今生，不清楚其来龙去脉，教学有如盲人摸象．

2.1 赌徒梅累的问题

概率论出身“卑微”是众所周知的，它很长一段时间得不到数学家们的普遍认同与它的出身或许有一定关系．但更重要的是，早期的概率论缺少严格的数学基础，这恐怕是概率论很长时间不能登堂入室的根本原因．一些数学史甚至没有把概率论列入其中，例如M·克莱因的《古今数学思想》[1]甚少提及概率论，这也许与这套巨著偏重于确定性数学有关．

掷骰子始于什么时候无从考证，但数学家研究这个问题还是有据可查的，发明了一元三次方程求根公式的16世纪意大利数学家卡尔丹（1501—1576）同时也是个赌徒，他曾说过一句：“诚实的骰子”，意思是说，掷骰子是公平的，机会均等，这是古典概型的基本前提．但掷骰子作为一个学术问题被数学家们研究可能最早开始于17世纪中叶，据说法国数学家帕斯卡（Blaise Pascal，1623—1662）在度假旅途中偶遇赌徒梅累，梅累向帕斯卡提出了一个分赌注的问题．梅累向帕斯卡介绍说，他在一次与赌友掷骰子时，每人押了32个金币，并事先约定：如果梅累先掷出3个6点，或其赌友先掷出3个4点，便算赢家．然而当梅累掷出两次6点，赌友掷出一次4点时梅累接到通知，要他马上陪同国王接见外宾，赌博不得不中断，但就此收回各自的赌注心有不甘，于是决定按照已经取得成绩分取这64个金币．但梅累与赌友不知道该如何分配这笔赌注．帕斯卡告诉梅累：如果再掷一次，甲胜，甲获全部赌注，乙胜，甲、乙平分赌注，两种情况可能性相同，所以这两种情况平均一下，甲应得赌金的3/4，乙得赌金的1/4．帕斯卡的回答或许让人一时难以理解，费马则给了一个令人信服的解答．首先把问题简化一下：甲、乙两人同掷一枚硬币，规定若正面朝上，则甲得一点，若反面朝上，则乙得一点，先积满3点者赢取全部赌注．假定在甲得2点、乙得1点时，赌局由于某种原因中止了，问应该怎样分配赌注才算公平合理．费马认为：结束赌局至多还要2局，结果为4种等可能情况：

情况 1 2 3 4

胜者 甲甲 甲乙 乙甲 乙乙

前3种情况，甲获全部赌金，仅第4种情况，乙获全部赌注．所以甲分得赌金的3/4，乙得赌金的1/4．显然费马的解答比帕斯卡的解答更容易理解一些．

2.2 古典概型

帕斯卡与费马虽然并未在研究这类问题时给出明确的定义，他们只是定义了使某赌徒取胜的机遇，也就是赢得情况数与所有可能情况数的比，这实际上就是后来人们定义的概率．对赌博问题感兴趣的人不只是帕斯卡与费马，1655年，荷兰数学家惠更斯在巴黎时了解到帕斯卡与费马的工作，也兴味盎然地参加讨论，这就是《关于赌博中的推断》（1657年）一书的由来，它是早期概率论的奠基之作．直到19世纪初，人们关于概率的研究大多限于古典概型，法国数学家拉普拉斯（1749—1827）在他的《概率的分析理论》一书中是这样定义概率的：“事件A的概率等于一次试验中有利于事件A的可能结果数与该事件中所有可能结果数．”古典概型有两个基本特征：（1）可能结果总数是有限的，用现在的语言叙述就是“样本空间”有限；（2）每个结果的出现有着同等的可能性，或者说样本空间中的点是等可能的．

由于贝特朗问题的出现使得人们对拉普拉斯的古典概型定义大肆抨击，这对拉普拉斯实在有点不公正，贝特朗问题研究的是无限样本空间情形，拉普拉斯说的是样本空间有限的情形，把贝特朗奇论的罪过归到拉普拉斯头上有点莫名其妙．在样本空间有限的情形，拉普拉斯的定义并无什么问题，否则类似掷骰子问题就不存在公平了，正如赌场出老千一样，在骰子里灌铅，或者在桌子下面放磁铁，掷骰子或转盘出现的数字显然就不是等可能的了，事实上，贝特朗问题在古典概型中是不会出现悖论的．贝特朗问题出现悖论是由于关注了随机试验结果的不同属性从而导致不同度量所带来的，而非样本空间的等可能性假设不同所致．这里不妨以掷骰子为例，假设骰子出现6个面是等可能的，也就是出现1到6六个数字的可能性是相同的，人们通常认为，相对于这个随机试验的所有可能结果即样本空间应该是{1, 2, 3, 4, 5, 6}，其中各个数字的出现是等可能的，所以每个数字出现的概率都是1/6．如果要计算出现某几个数字的概率，直接用出现这些数字的可能结果与结果的总数去比就可以了，例如出现偶数的概率与出现奇数的概率都是1/2．但如果机械地理解古典概型与随机试验的样本空间就会导致贝特朗问题的争论．

假设立方体（骰子）的6个面分别标注1至6六个不同的数字，只要立方体的材质密度分布均匀，出现6个数字的可能性可以认为是相同的，这也叫无差别原则．这时的样本空间为{1, 2, 3, 4, 5, 6}，如前所述，可以计算出出现奇数的概率与出现偶数的概率均为1/2．现在换一种说法，把1、3、5三个数字用黑色的颜料涂抹掉，将2、4、6三个数字用白色的颜料涂抹掉，随机掷这个只有黑白两色的骰子，出现每个面的可能性是相同的，这时的样本空间是什么？显然是{黑色，白色}，出现黑色的概率与出现白色的概率均为1/2．除了把六面体的数字用黑白两色涂抹掉，骰子的随机性并没有发生改变，但样本空间却不同了．人们通常认为{1, 3, 5}是一个随机事件，其概率可以根据1、3、5出现的概率来计算，3个点的概率相加，自然是1/2．

在一个随机试验中，可能出现具有多种属性的结果，如果你关心的某种属性没有共性，那么所有可能的结果都是样本点，如果你关心的某种属性具有共性，也可以将具有共同属性的结果放在一起作为样本点．上面的随机试验说明，当你关心的是骰子的每一面出现的具体数字，而这些数字又是互不相同的，那么样本空间就是可能出现的每一个数字，例如上面的{1, 2, 3, 4, 5, 6}．如果关心的是这些数字的某种共同属性，例如奇偶性，那么可以将这种共同的属性作为可能的结果，即样本点，具体地说，如果上面掷骰子试验关心的是数字的奇偶性，那么样本空间可以看成{{1, 3, 5}, {2, 4, 6}}或者{奇数，偶数}．这里蕴含着分类的思想，将同为奇数的数字放在一起看成一点，同为偶数的数字放在一起也看成一点．这就是分类的思想，即将奇数与偶数各自分成一类．如果不理解分类思想，就无法理解贝特朗问题的3种不同解答．

即使是样本空间有限的情况下关注随机试验结果的不同属性也可能导致不同的概率问题．以摸球问题为例，假设箱子里有7个分别标注有1到7不同数字的球，形状、大小、质地都一样，随机从箱子里摸一只球，出现每个数字的概率都是1/7．如何计算出现奇数与偶数的概率？一种方法是传统的，把奇数偶数都看成样本空间的子集，即随机事件，然后计算其概率，另一个办法与前面类似，把7个数字按奇数与偶数分类，则得到样本空间{奇数，偶数}，但这时候的样本点显然不是等可能的，出现奇数的概率为4/7，出现偶数的概率则为3/7，按定义，这就不是个古典概型．由此可见关注随机试验结果的不同属性可能导致不同的概率问题．但对于有限的样本空间来说，只要随机假定是一样的，无论采用哪种方法，不会出现不同的答案，也就是说不会产生类似贝特朗问题的悖论．这是因为有限样本空间中的度量方法是统一的，都是计算所有可能结果的数量．这个问题对于实际生活有意义吗？其意义是不言而喻的．例如，工商管理部门要抽检市场上几个不同品牌的同类产品，如何抽取样品？比较公平合理的做法是根据各品牌投放市场的总量按比例抽取一定数量的样品，这样得到的合格率才是客观可信的．举例来说，厂商甲投放了100万件，厂商乙投放了50万件，这时工商部门分别从两个品牌中各抽检1 000件显然是不合理的．

2.3 统计意义下的概率定义

古典概型要求样本空间是有限的，雅各布·贝努利认为：“这种方法仅适用于极罕见的现象．”他主张通过观察来确定结果数目的比例，这或许可以认为是统计意义下概率的早期定义．贝努利说：“即使是没有受过教育与训练的人，凭天生的直觉，也会清楚地知道，可利用的有关观测的次数越多，发生错误的风险就越小．”在古典概型下，贝努利证明：“当试验次数越来越大时，频率接近概率．”这个论点不仅适用于古典概型，也适用于更一般的情形，1919年，德国数学家冯·米塞斯（1883—1953）在其《概率论基础研究》一书中提出了概率的统计意义上的定义：“在做大量重复试验时，随着试验次数的增加，某个事件出现的频率总是在一个固定数值的附近摆动，显示出一定的稳定性，把这个固定的数值定义为这一事件的概率．”这个定义的确摆脱了“等可能性”假设的束缚，它适用的范围更广泛．

然而，等可能性假设并非一个脱离经验的单纯主观假设，焉知掷骰子出现各个数字是等可能的假设不是一个统计意义下的结果？赌场规则虽然是一种人为的约定，但这样的约定要得到广大赌徒的认同必定有基于经验的成分，正是在多次掷骰子的重复试验中发现了这样的规律．也就是说，拉普拉斯关于古典概型的定义应该也是基于人的直觉，并非拉普拉斯的主观约定．正如一个箱子里有7个球，其中4个黑色，3个白色，只要7个球外形、大小都是一样的，随机从箱子里摸球，不可能有人认为出现黑色与出现白色的概率相同，这不是基于理论的推导，而是经验判断．

中学阶段虽然不学一般意义下的概率，但教师在介绍频率与概率的关系时至少应该向学生说明几个问题：（1）“频率接近概率”只有在样本量非常大的情况下才有意义，任何有限的实验数据中，其频率与概率很可能相距甚远．（2）很多概率的估算可能不是大量重复试验的结果，例如炮弹合格的概率不可能根据频率来估算，只能是通过有限的试验再结合工程师的经验以及制造炮弹的各种参数来判断．再如天气预报一般也并非根据某种气象出现的频率来估算该现象出现的概率是多少，而是根据各种气象数据综合分析得出的结论．

2.4 公理化的概率论

（1）公理化概率论的缘起．

在公理化概率论诞生前，概率论一直遭人诟病，以至于始终不能为数学家们普遍接受．1900年的国际数学家大会上，希尔伯特（1862—1943）提出的23个著名问题中，建立概率论的理论基础便是其中之一（希尔伯特第六问题），但希尔伯特没有将它放在数学类，而是放在数学物理类．

自从希尔伯特倡议建立概率论的公理化基础之后，很多数学家开始为概率论寻找它作为数学而“存在”的理由．数学史上完全从不同的角度研究同一类问题或者研究不同的问题却采用了类似方法的例子十分常见．就概率论而言，它最终能堂而皇之走进数学殿堂成为数学的一个重要分支跟那个时期数学的发展有着密切关系．很难想象，如果没有勒贝格（Lebesgue，1875—1941）发明的测度论（虽然这之前关于测度的研究已经有很多，特别是波莱尔测度对数学的影响很大，迄今依然经常为人们使用，但都很不完善，波莱尔的学生勒贝格的工作几乎取代了前人所有的工作），还能有后来柯尔莫哥洛夫（Kolmogorov）的伟大工作．20世纪30年代，柯尔莫哥洛夫正是基于测度论为概率论建立了一套公理体系，从而给一直不能跨进数学之门的概率论奠定了严密的数学基础，使得概率论成为数学殿堂中名正言顺的一员．

试图对中学生讲清楚公理化概率论恐怕是一件异想天开的事，即使是曾经在大学学过概率论的中学教师，他们中的大多数人可能也不清楚公理化概率论为何物，因为早期大学的概率论教材很多并不介绍公理化的概率论，仅仅局限于微积分意义上的连续型分布，其分布密度函数是一个非负的黎曼可积函数．但作为教师，不了解概率论的前世今生而去教概率论似乎是一件不可思议的事情，事实上，经典的几何概型不仅存在类似贝特朗问题的理解上的歧义，概念也是很不严谨的．这里采用通俗的方式介绍一下什么是公理化的概率论，以便读者对这一理论有一个大概了解，从公理化的概率论便可以看出几何概型的漏洞在哪里．

回顾一下，无论是古典概型还是几何概型，计算随机事件的概率时都需要采用合适的度量方法去测量样本空间子集的大小．古典概型使用的是计数方法，即用随机事件可能的结果数量去比所有可能结果（样本空间）的数量．几何概型情形下样本空间是无限的，用随机事件可能的结果数量作为度量显然是没有意义的．所以需要使用不同的度量方法，一维情况下使用长度，二维情况下则使用面积．无论是古典概型使用随机事件可能结果的数量还是几何概型中使用长度或面积，他们都有一些共同的特点．不妨用X表示样本空间（有限或无限），E表示随机事件（样本空间的子集），(E)表示随机事件E的概率，那么(E)有这样几个特征：

（1）对任意X的子集E，有(E)≥0，(ф)=0；

（2）(X)=1；

（3）如果E、F是X中两个互不相交的子集，则(E∪F)=(E)+(F)．

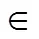
(∪=1∞E)=Σ=1∞(E)？

这个等式称为可数可加或可列可加．可以证明，如果可加性恒成立，那么可数可加性必定也成立，有兴趣的读者要证明这件事并不困难，或者可以从任何一本实变函数书籍中找到答案．因此问题的关键是可加性是否恒成立？或许你以为这个问题再平凡不过，先别急于下结论，姑且回头来重新审视一下样本空间及其随机事件．假设随机试验的样本空间是开单位圆盘，样本点遵循无差别原则，按照几何概型的一般解法，随机事件E的概率(E)等于该事件所有可能结果所形成区域E的面积(E)与单位圆的面积(D)之比，即

(E)=(E)/(D)．

一切显得如此自然，似乎没什么问题．现在不妨深究一下：相对于样本空间单位圆盘，其事件域是什么？是开圆盘的一切子集还是部分子集？哪部分子集？教师在教学过程中交代清楚了吗？理论上讲，飞镖落在圆盘的任何位置都是可能的，如果问：“假设E是圆盘内坐标为有理数的点，飞镖落在E中的概率是多少？”这个问题在数学上并非没有意义，因为既然做了等可能性假设，一切皆有可能．可是在这里，E的面积是什么？有定义吗？甚至可以假设E为圆盘内的任意子集，然后问飞镖落在E中的概率是多少？这时(E)又是什么？这说明经典的几何概型概念是不严密的，几何概型中样本空间的事件域并不清楚．测度论的诞生是概率论之大幸，如果没有测度论，概率论的这一致命伤恐怕迄今无法补救，是勒贝格与柯尔莫哥洛夫拯救了概率论．

（2）公理化概率论的诞生．

从几何概型可以看出，概率的定义依赖于“面积”的定义，所以关键是如何定义一般集合的“面积”，所谓一般集合的“面积”即是测度．遗憾的是，在一个具有不可数个点的空间（例如直线上的某个线段或平面内的某个区域）中无论怎么度量集合，在这个度量下，总会有一些集合是不满足可加性的，如果没有可加性，所谓概率就无从谈起，因为如前所述，可加性是概率的基本特征．因此，不能指望对样本空间的所有子集定义测度，而只能对其中部分子集定义测度，也就是那些满足可加性的集合，这就是可测集的由来．有一个问题是自然的，样本空间中有多少集合不满足可加性？很不幸，非常多，与可测集一样多，不过要搞清楚这个问题需要一点集合论与测度论的专门知识，这里就不赘述了，有兴趣者可以参考实变函数或测度论的相关书籍．

具体到一般的样本空间，对于给定的样本空间X，其事件域是什么呢？它是由X中的某些（未必是全部）子集构成的集合F，这个集合需要满足几个基本条件：

（1）空集ф与全空间X在F中；

从前面的分析可以看出，要求F中的元素满足上述3点是自然的，将满足（1）-（3）的集合称为由X中子集构成的-域，也把F中的元素称为可测集，通常把(X, F)称为可测空间．由此可见，可测空间并不依赖于具体的测度．但一般情况下，如果用到可测集，当然就需要给它一个测度，这个测度应该满足：

（1）(E)≥0，(ф)=0（非负性）；

换句话说，只要满足（1）与（2），就说它是可测空间(X, F)上的一个测度，所以测度不是唯一的，对应到同一个F，可以定义多种测度．但如果研究一个测度空间（概率空间）则通常与具体的测度有关，或者说测度空间涉及3个要素：空间（样本空间）X、-域（事件域）F、测度（概率），把(X, F,)称为测度空间．

那么概率与测度有何不同？回顾概率的定义，概率不仅需要满足非负性、可加性，还需要满足全空间的概率为1，因此如果测度空间(X, F,)除了满足上面的（1）和（2），还满足：

（3）(X)=1，则称为概率测度，简称为概率，(X, F,)称为概率空间．简而言之，所谓概率测度即归一化的测度（全空间的测度为1），这就是所谓的公理化概率．

从公理化的概率定义可以看出，先有样本空间才有事件域，最后才有概率，对于同一个样本空间与事件域，概率分布可能有多种．相对于具体的随机试验，其样本空间未必唯一，关键要看关注随机试验结果的何种属性，这在古典概型情形下已经做过阐述．所以在研究概率问题时首先需要确定样本空间、事件域及概率．在同一个随机试验中，如果试验的结果存在不同的属性，样本空间可能有多个，如何确定随机试验的样本空间才是合理的？在没有特别说明的情况下，样本空间不应该根据随机性假设来确定，而应根据问题的目标来确定，也就是说根据所关注随机试验结果的属性来确定样本空间，当样本空间确定后，谈概率问题才是有意义的．按照目标确定随机试验样本空间的原则，如果在一个随机试验中事先给出了随机假定，那么即使是一种等可能性假设，也未必导出古典概型或几何概型．由于在中学阶段仅限于古典概型与几何概型，所以不宜将类似贝特朗奇论容易产生歧义的概率问题放到中学从而造成人为的陷阱，甚至产生相互矛盾的结果．教材中飞镖问题的解答与教辅材料（参见文[2]）中从直角三角形的直角顶点向斜边随机引射线问题的解答就是典型的两种相互矛盾的解答，因为飞镖也可以看成从掷镖人手中发出的射线，这无疑大大增加了学生对概率的理解难度．

现在按公理化概率论重新审视一下几何概型，不妨假设样本空间是单位圆盘，相对于这个样本空间的事件域是什么？显然不可能是圆盘的所有子集构成的集合，否则无论怎么定义测度，总会有一些子集是不可测的．按照勒贝格的测度论，此时合适的事件域是圆盘中所有勒贝格可测子集全体，记为(D)，测度可以是通常的勒贝格测度，它是面积概念的自然推广，对应的测度空间就是(D,(D),)，将勒贝格测度归一化，就得到概率空间了．或者按照几何概型通常的做法，对任意E∈(D)，E的概率(E)=(E)/(D)．

对于勒贝格测度有兴趣但又不想了解太深入的读者不妨参考克莱因的《古今数学思想》第三册第44章．

3 重组概率论课堂教学

数学教育应该遵循几个基本原则：（1）适应学生的认知水平；（2）在尊重历史的基础上改进教学内容；（3）杜绝伪情境．就概率而言，首先要帮助学生解决的一个重要问题是认识随机现象，进而定义随机事件．不妨就从掷骰子问题开始．例如可以通过如下一些问题展开．

问题1 如果抛一个骰子（或任何物体），骰子会落向哪个方向？地上还是天花板？

这显然是一个必然事件，因为万有引力的作用，骰子一定会落到地上．

问题2 假设骰子是一个正立方体，6个面上分别刻有1、2、3、4、5、6六个数字，并且骰子的密度是均匀的，如果抛这个骰子，当骰子落到地上时，能确定哪个数字朝上吗？能确定是偶数朝上还是奇数朝上吗？

学生回答这个问题不会有任何困难，而且学生凭借生活经验多半也能判断，出现任何数字的可能性是相同的．退一步说，如果学生不能发现出现任何数字的可能性是相同的这一规律，教师可以进一步引导学生分析问题中的条件“骰子的密度是均匀的”意味着什么？问题2中最后一个问题无疑在暗示学生，在一个随机试验中，随机事件有两种类型：基本事件以及由若干基本事件组成的随机事件，基本事件是特殊的随机事件．

问题2虽然不那么高雅，但它确实是一个真实有效的问题情境，也与概率的“身世”相吻合．如果觉得这个问题不够高大上，还可以换一个问题．

问题3 学校为了检查每个班的体育锻炼情况，决定从每个班级任意抽调一位同学去参加体育测试，为了反映班级真实情况，不得有选择性地抽调同学．请问比较合理的抽调方法是什么？

这个问题比问题2稍微困难一点，因为需要学生自己想出“合理”的方案．对于高中生而言，他们有足够的能力回答这个问题：抓阄．假设班级有50个人，准备50张小纸片，其中一张纸片上写着参加，另外49张纸片上写着不参加，可以设计这样几个引导式的问题：

（1）能肯定哪个同学一定抽到参加的纸片吗？

（2）每个同学抽到参加的可能性是否相同？

由于历史上出现得最早的概率问题正是古典概型，所以没有必要急于让学生了解一般的随机事件，就针对古典概型来讨论就可以了．

通过上述几个问题的讨论，学生对必然事件、随机事件已经有了初步认识，在此基础上不妨给出古典概型的严格定义．同时，应该给出基本事件、样本空间及随机事件的数学定义．什么叫基本事件？不能简单地用随机试验所有可能的“基本结果”来定义基本事件，因为并没有给出基本结果的定义．为了说清楚基本事件，不妨引入互斥事件的概念，这在理解上并无任何困难：“两个不可能同时发生的随机事件称为互斥事件．”当然，不作这种调整也不妨碍对基本事件与随机事件的理解．按照标准的定义，随机试验所有可能的结果组成的集合称为样本空间，每一个可能的结果都称为基本事件或样本点．教材中正是因为将“在一定条件下，可能发生也可能不发生的结果称为随机事件”导致后面对基本事件的定义带来了含混．基本事件应该满足两个基本条件：（1）任何两个基本事件是互斥的；（2）任何随机事件都可以表示成若干基本事件的和（即若干基本事件组成的集合）．基本事件A与B互斥即指若A发生则B不可能发生，反之亦然．可以通过掷骰子中任何两个数字不可能同时出现来说明这个问题，或者通过同学抓阄时不可能既抓到参加的纸片又抓到不参加的纸片说明．

初识样本空间、基本事件以及随机事件之后，需要对基本事件与随机事件加以辨析，也就是什么叫任何随机事件都可以表示成若干基本事件的和？仍然可以通过掷骰子来说明，例如可以进一步设计这样的问题．

问题4 随机掷一枚骰子，如果问出现偶数的概率是多少，这时所指的随机事件是什么？如何计算该随机事件的概率？

有了以上的讨论，可以由学生自己提供一些随机现象的例子，善于思考的学生也许不仅仅想到掷硬币，样品抽检之类的随机现象，甚至可能想到天气、地震之类的现象也是随机的，但这些随机现象就不是上述方法可以处理的了．

清楚了古典概型及其概率的计算，接下来的单元是几何概型，这是教学中的难点，教材中几何概型的定义是不严格的，给出一般的几何概型定义并不会增加学生对几何概型理解的困难，几何概型的难点在计算而不是概念，所以教材应该给出严格的数学定义．课堂上可以通过类似下面的问题展开．

问题5 士兵在练习实弹射击时，能肯定子弹会射中靶子上的哪一点吗？

这与掷飞镖本质上是一个问题，而且现实的扔飞镖与实弹射击都不是几何概型，不过，不妨假设掷镖人或士兵是初学咋练，镖或子弹射中靶子的任何一点是等可能的，这个问题也为后面引入非等可能性概率问题埋下伏笔．通过这个问题的讨论，可以引出样本空间无限的概率问题．即

定义 如果一个随机试验所有可能的结果有无限多个，且每一种结果都是等可能的，则称这样的概率模型为几何概型．

在此基础上可以引导学生找出一些几何概型的例子，包括一维、二维甚至三维情形下的几何概型．在学生对几何概型有了比较多的了解后，有必要向学生说明几何概型未必如想象的那样一定是空间中某些区域构成的样本空间，但不宜太详细，因为以学生的知识积累尚不足以理解一般的无穷集以及测度，教师如果清楚，可以做科普式的介绍，不清楚则一带而过．

无论是教材还是在课堂都不宜将类似教辅材料（参见文[2]）中从直角三角形直角顶点随机引射线等问题放在中学阶段学习，这会引起学生对几何概型的困惑，只有当学生在概率方面有了相当的素养后才适合研究那类问题．具体地说，中学阶段的概率问题最好都是样本空间比较容易明确的那些问题，设置一些类似贝特朗问题的陷阱并不能给学生理解概率带来任何实质性帮助，即使作为课外参考，也不应该与教材在逻辑上相悖．例如教材中掷飞镖等问题也可以理解成从掷镖人手中随机抛出的射线，按照这样的逻辑来理解，很多概率问题都会带来歧义甚至是不可解的．例如随机抛一粒沙子的问题就不是中学生能解决的，如果抛沙子的角度不定，问题就不可解．解决这个问题的比较好的办法是命题人在拟定题目时将目标（随机事件的概率）与等可能性假设相一致．正如掷飞镖问题中，因为目标关注的是飞镖的着靶点，所以针对靶子上的点做等可能性假设比较合适，否则掷镖人站在不同的位置，就会得到不同的概率问题．在学习了一般的概型之后再适当研究这类问题并无不可，只是这些问题不适合中学生．

概率必修教材在几何概型之后便是互斥事件，如果不讲选修内容，概率到互斥事件就算结束了．仅就必修教材的编写看，概念的定义稍显粗糙，逻辑也不够严谨．可以考虑首先介绍一般的随机试验，然后定义随机事件与互斥事件，在此基础上定义基本事件与样本空间，再介绍古典概型与几何概型．按照这样的体系编写既符合概率论发展的历史脉络，概念也不失严谨．

说到选修2-3中的概率章节，教学内容可能需要做比较大的改进．

学生对随机现象与随机事件已经有所了解，没有必要每章每节开头必要以不同的“生活化”例子开头，好的例子可以反复使用，从不同的角度进行研究．为了引入随机变量，首先需要引导学生思考，如何利用数学语言表示现实中的随机现象？或者说如何用符号化的语言表示随机现象或随机事件？不妨还是从掷骰子开始．

问题6 首先回忆一下在利用数学方法研究确定性实际问题时，首先要做的一件事是什么？掷骰子试验的样本空间是什么？如何用合适的方法表示掷骰子试验？

问题7 抛硬币试验的样本空间是什么？如何用数学方法表示这个试验？

问题8 如果知道了随机试验的样本空间，如何用数学方法把这个试验表示出来？

通过上述3个问题的分析，不难逐步引入随机变量的概念，完全没有必要通过左一个右一个的例子做直观的阐述，可以给出随机变量的严格数学定义，直观解释可以帮助学生理解概念，但不能代替概念的严格定义．

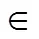
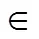
问题10 在掷骰子试验中，样本空间为{1, 2, 3, 4, 5, 6}，如何用随机变量表示出现偶数或奇数的随机事件？

限于篇幅，对于更一般的随机试验将另文讨论．

[1] M·克莱因．古今数学思想（第三册）[M]．上海：上海科学技术出版社，2014：201-210．

[2] 高中新课程学习指导编写组．成才之路（数学必修3）[M]．北京：中国和平出版社，2012：64-65．

On the Teaching of Probability in Middle School from the Perspective of Historical Development

ZHANG Shu-qing1, CAO Guang-fu2, LUO Li-ling2

(1. Zhixin High Middle School, Guangdong Guangzhou 510095, China;2. Faculty of Mathematics and Information Science, Guangzhou University, Guangdong Guangzhou 510006, China)

In the context of historical development, this paper made a brief and concise exposition of the development of the theory of probability from the probability of classical probability to statistics and then to the probability theory of axiomatic. It was convenient for teachers to have a preliminary understanding of the basic history of probability theory. At the same time, through the creation of a series of problem situations, it put forward some practical suggestions for the teaching of random events, sample space, classical probability and geometric probability model in the middle school class. The article thought, probability teaching should follow a few basic principles: 1, adapt to the student’s cognition level; 2. Improving teaching content based on respect for history; 3. No false situations. It also argued that the definition of concepts should be accurate and the logical relationship between different concepts (basic events, sample spaces, random events) should be clear. In high school, it was not appropriate to design some trap of Bertrand problem, which, apart from increasing the difficulty of students’ understanding of geometrical models, did not help students’ learning probabilities.

random events; sample space; classical probability; geometric probability model

[责任编校：周学智]

2018–04–19

国家“万人计划”领军人才、广东省“特支计划”、广州市教育名家工作室联合资助

张蜀青（1973—），女，广东广州人，高级教师，博士生，主要从事中学一线教学与数学教育研究．

G420

A

1004–9894（2018）04–0035–06

张蜀青，曹广福，罗荔龄．从历史发展的视角看中学概率教学[J]．数学教育学报，2018，27（4）：35-40．