合理选择主元解决一类方程整数根的问题

☉江苏省无锡市第一女子中学秦唯超

初中数学中方程整数根的问题，按常规解法往往需要考虑多个方面，计算量大，步骤繁多，让大部分学生望而生畏.如果对这些司空见惯的常规解法进行再思考，跳出定式思维，改变思考问题的角度，也许我们能够收到意想不到的效果.

高中数学解题中“主元思想”的应用是非常普遍的，但是，在初中数学解题中并不常见.其实，主元思想对初中生来说并不陌生.比如，当一个方程中存在两个字母时，我们常常规定这个方程是“关于x的”某个方程，而将另一个字母视作待定系数或常量，这就是一种“主元思想”.在解决含有多个字母（元）的数学问题的过程中，选择其中一个字母作为研究的主要对象，即视其为主元，而将其余字母视作参数或常量，从而达到简化过程的解题思想即为“主元思想”.

本文就几个典型例题的分析和解题研究，简单介绍一下如何合理选择主元、运用主元思想解决一类方程整数根问题.

例1关于x的一元二次方程x2+2x+2k-4=0有两个不相等的整数根，求正整数k的值.

分析：原方程中含有x和k两个字母，常规解法是将方程视作以x为主元的一元二次方程，利用根的判别式作为切入点解决问题.如果将k看作主元，则可以将方程降阶为一元一次方程，或许能更快地解决问题.

解法1：由关于x的一元二次方程有两个不相等的根，得Δ=4-4（2k-4）＞0，则k＜.

又k为正整数，则k=1或2，

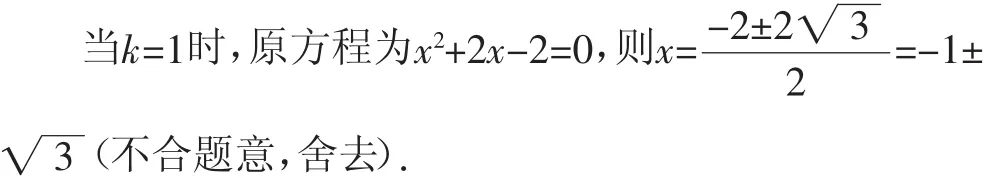
当k=2时，原方程为x2+2x=0，则x1=0，x2=-2（符合题意）.

综上所述，k=2.

解法2：将k看作主元.将原方程整理成以k为主元的方程，得2k+x2+2x-4=0，则k=为正整数.

又x为整数，则（x+1）2=1.

则x+1=±1.

则x1=0，x2=-2（符合题意）.

则k=2.

点评：从例1可以看出，首先要确定主元，一旦选定主元，就明确了解题的主要方向.本题将k看作主元的这种换位思想，由于直接降阶，解法比常规解法更简洁.

例2已知方程x2+mx-m+1=0有两个不相等的正整数根，求m的值.

分析：将x视作主元，从一元二次方程根的判别式入手的常规解法，肯定是可以解决问题的，但是没有明确m取哪一类数，所以需要进一步判断.而将m看作主元，得到的是含x的待定系数方程，要进行分类讨论.到底哪一种方法更好，实践出真知.

解法1：由关于x的方程有两个不等根，得Δ=m2-4（-m+1）=m2+4m-4＞0.

方程有两个正整数根，不妨设为x1、x2，则x1+x2=-m是正整数；则m2+4m-4是完全平方数.

不妨令m2+4m-4=n（2n为正整数）.

则（m+2）2-8=n2.

则（m+2+n）（m+2-n）=8.

解法2：将m看作主元.

将原方程整理成以m为主元的方程，得（x-1）m+x2+1=0 （*）.

当x=1时，（*）显然不成立.

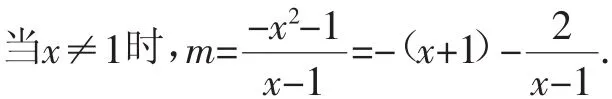
方程有两个正整数根，不妨设为x1、x2，则x1+x2=-m是正整数.

则m是负整数.

则x-1=±2或±1.

则x=3、-1（舍）、2或0（舍）.

则m=-5.

点评：从例2可以看出，常规解法从考虑根的判别式入手，兼顾奇偶性，过程比较繁杂；而将m看作主元的方法，灵活、机敏地挖掘出了问题的本源，达到了“出奇制胜”的效果.

例3关于x的方程（a-1）x2+2x-a-1=0的根都是整数，则符合条件的整数a有____个.

分析：不管是将x视作主元，还是将a视作主元，都是待定系数方程，必须进行分类讨论.将a视作主元的方程中，待定系数出现了二次，可能会给解题设置一定的障碍.

解法1：当a=1时，x=1.

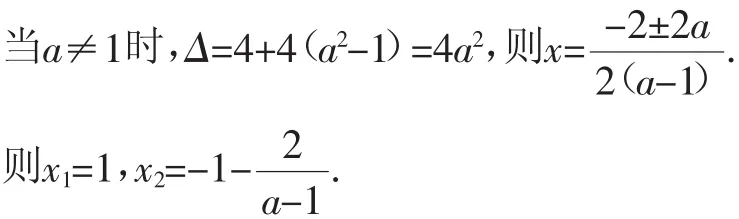
由方程的根都是整数，得1-a=±1或±2.

则a=0、2、-1或3.

综上所述，a=1、0、2、-1或3，共有5个.

解法2：当a=1时，x=1.

当a≠1时，将a看作主元.

将原方程整理成以a为主元的方程，得（x2-1）a-x2+2x-1=0 （*）.

①当x=-1时，（*）显然不成立.

②当x=1时，（*）恒成立，是原方程的一个固定根.

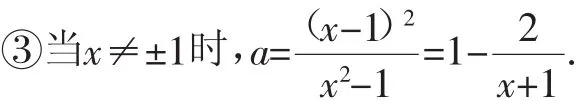
由方程的根都是整数，a是整数，得x+1=±1或±2.则a=0、2、-1或3.

综上所述，a=1、0、2、-1或3，共有5个.

点评：从例3中可以看出，由于原方程有x=1这个固定根的存在，且Δ=4a2从形式上看就是一个简洁的完全平方式，将x看作主元的常规解法显得更为简洁.所以，不必拘泥于以哪个字母作为主元，更有利于优化解题，我们就选择哪一个.

例4关于x的方程ax2+2（a-3）x+（a-2）=0至少有一个整数根，求整数a的值.

分析：不管将哪一个字母作为主元，都是待定系数方程，必须分类讨论，并且，方程给出的条件是至少有一个整数根，所以以x为主元的常规解法必须针对这一条件进行讨论，可能比较复杂.而以a为主元的解法或许能柳暗花明又一村.

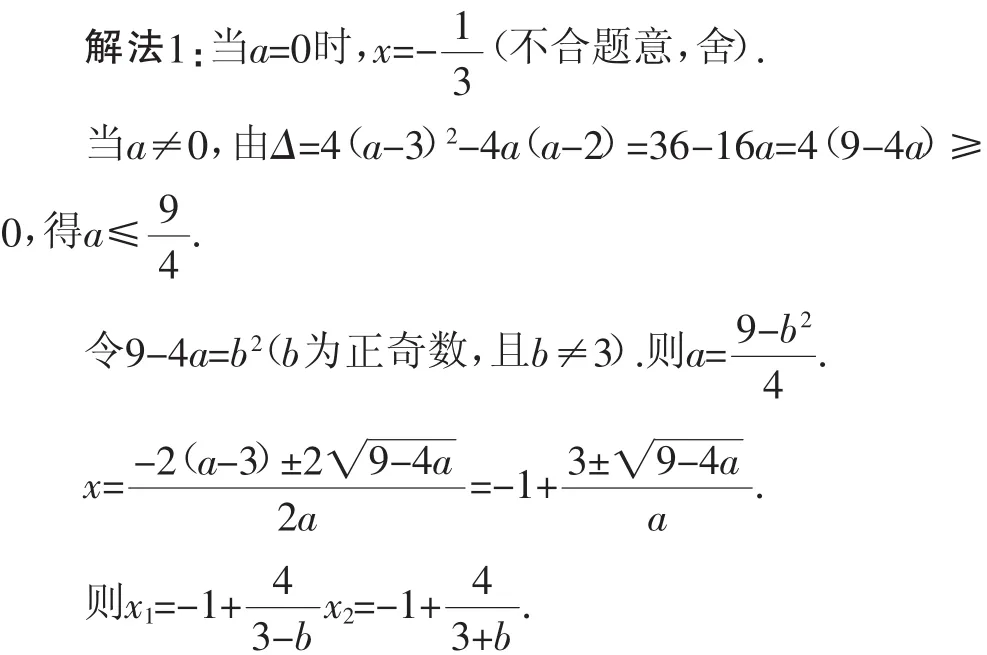
①当x1为整数，b为正奇数时，3-b=±2-4.则b=1、5或7.

②当x2为整数，b为正奇数时，3+b=4.

则b=1.

综上所述，b=1、5或7.

则a=2、-4或-10.

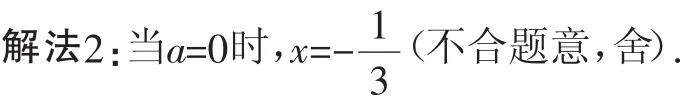
当a≠0时，将a看作主元.

将原方程整理成以a为主元的方程，得：（x2+2x+1）a+（-6x-2）=0 （*）.

①当x=-1时，（*）显然不成立.

由原方程至少有一个整数根，得x+1=±1、±2.

则a=2或-10或-4（经检验，符合题意）.

点评：当方程的整数根至少有一个时，以a为主元的解法有效避免了对根的讨论，挖掘出了题目的特殊性，大大简化了解题过程，达到了化繁为简的目的.

主元思想，是一种重要的数学思想，它发源于“解决问题抓主要矛盾和矛盾的主要方面”这一哲学思想.通过实例我们可以看到，在含有两个变量的方程问题中，跳出定式思维，合理选择主元，运用主元思想对方程进行整理和变形，从两个变元中选择一个作为主元，让解决问题的目标和方向更明确、清晰，往往能够达到“化繁为简、直达目标”的效果，优化我们的解题过程.用主元法，在初中阶段，不仅在解决方程整数根的问题中可以使用，其实还有许多用武之地，比如，分解因式、等式或不等式的证明、对称式等问题中都能见到它的身影.总之，数学研究和学习，有序逻辑推理是根本，这取决于思维的起点和关键点，而主元思想正站在这样一个点上.W