矩阵秩的求解方法及应用探索

李燕娟

(兰州交通大学博文学院，兰州 730000)

1 矩阵秩的定义及性质

由文献[1]，给出k阶子式、矩阵秩的定义及矩阵秩的性质：

定义1：在m×n矩阵A中，任取k行k列(k≤m,k≤n)，位于这些行列交叉处的k2个元素，不改变它们在A中的位置次序而得的k阶行列式，称为矩阵A的k阶子式。

定义2：设在矩阵A中有一个不等于0的r阶子式D，且所有高于r阶的子式(如果存在的话)全等于0，那么D称为矩阵A的最高阶非零子式，数r称为矩阵A的秩，记作R(A)=r，并规定零矩阵的秩为0。

讲解时，强调“有1个”r阶子式不等于0，“所有”高于r阶的子式全等于0，说明高于r阶的子式可能不存在(比如r阶方阵的行列式不等于0，此时不存在高于r阶的子式)。

注：矩阵A的秩R(A)就是A的非零子式的最高阶数。

讲解矩阵秩的概念后，给出3个问题让学生们思考：

(i)若R(A)=r，是否所有r阶子式都不等于0？(否，因为有1个即可。)

(ii)若存在r+1阶子式等于0，是否有R(A)=r？(否，因此要求所有，而不是存在。)

(iii)若所有r+1阶子式等于0，是否所有高于r+1阶子式全等于0？(是，可以由行列式按行(列)展开定理保证。)

由矩阵A秩的定义，可得到矩阵的秩具有下列性质：

(i)若A为m×n矩阵，则0≤R(A)≤min{m,n}；(由定义1和2可得)

(ii)R(A)=R(AT)；(由行列式的性质行列式与行列式的转置相等及定义2可得)

(iii)n阶方阵可逆的充要条件是R(A)=n。(由矩阵A可逆的充要条件|A|≠0及定义2可得)

由此可见，可逆矩阵的秩等于矩阵的阶数，不可逆矩阵的秩小于矩阵的阶数。因此，可逆阵(非奇异阵)又称满秩矩阵，不可逆阵(奇异阵)又称降秩矩阵。

2 矩阵秩的求解

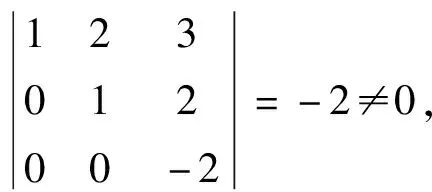
由例1可知：

(i)对于r阶方阵A，若其行列式不等于0，则R(A)=r满秩，否则，寻求是否有1个r-1阶子式不等于0。若有1个r-1阶子式不等于0，则R(A)=r-1，否则，寻求是否有1个r-2阶子式不等于0，以此类推……

(ii)对于一般的矩阵，当行数与列数较高时，按定义求秩很麻烦。然而对于行阶梯形矩阵，它的秩就等于非零行的行数，一看便知。因此，自然想到利用初等变换把矩阵化为行阶梯形矩阵。

问题：初等变换前后两个等价矩阵的秩是否相等呢？

定理[2]：矩阵的初等变换不改变矩阵的秩。

由定理，为求矩阵的秩，只要把矩阵用初等行变换变成行阶梯形矩阵，行阶梯形矩阵中非零行的行数即是该矩阵的秩。

解：将A进行初等行变换化成行阶梯形矩阵，

∴R(A)=3

解：先对矩阵A进行初等行变换化成行阶梯形矩阵，

∵R(A)=2，∴第三行元素全为0，因此m=6,n=27。

矩阵求秩除了定义法和化行阶梯形矩阵法，还可利用Matlab等数学软件求解。比如对于例2，只需在Matlab中编写程序：

clear all; clc

A=[1,1,1,0;1,2,3,-1;2,-1,0,1;2,3,0,1]

B=rank(A)

按Enter键，即可输出矩阵A和A的秩B=3。

3 矩阵秩的应用

矩阵秩的应用领域很广，如：可以用来判定方阵是否可逆、判定向量组的线性相关性、判定线性方程组解的情况，等等。下面就矩阵的秩在判定向量组的线性相关性和解线性方程组中的应用进行阐释。

(1)当m+12=0，即m=-12时，R(A)=2<3，则向量组α1,α2,α3线性相关。

(2)当m+12≠0，即m≠-12时，R(A)=3，则向量组α1,α2,α3线性无关。

注：该题也可利用行列式是否为零来判定向量组的线性相关性。

解：对系数矩阵A进行初等行变换，首先化成行阶梯形矩阵，

∴R(A)=2<4，因此该方程组有非零解。进一步对矩阵进行初等行变换化成行最简形矩阵，

注：从此例中，我们看到3个方程构成的线性方程组，系数矩阵的秩为2，“真正起作用”的只有2个方程，即线性方程组中系数矩阵的秩等于“真正起作用”的方程的个数。

为了提高学生的学习兴趣，对学生进行思政教育，在此引入《韩非子·内储说上》中“滥竽充数”的故事：“齐宣王使人吹竽，必三百人。南郭处士请为王吹竽，宣王说之，廪食以数百人。宣王死，湣王立。好一一听之，处士逃。”故事中的南郭先生无真实才学，300人中真正会吹芋的只有299人。这个300人的乐队，如果看作一个由300个方程构成的线性方程组的话，“真正起作用”的只有299个方程。此时，教育学生唯有勤奋好学，脚踏实地，学得真本领，将来才能真正做个对社会有用的人，方可立于不败之地。

4 结语

从矩阵秩的定义着手，深入剖析矩阵秩概念蕴含的意义，多角度深层次阐释矩阵的秩。首先由定义求解矩阵的秩，进而针对实际求解中可能遇到的问题，发现行阶梯形矩阵非零行的行数等于矩阵的秩，因此对矩阵进行初等行变换化成行阶梯形矩阵，从而获得矩阵的秩。由不含未知参数和含未知参数两种情况举例说明。为了适应信息时代的发展，文中给出了利用Matlab软件求解矩阵秩的方法步骤。最后给出了矩阵秩的应用，分别举例说明矩阵的秩在判定向量组的线性相关性和求解线性方程组中的实际应用。为了阐释矩阵的秩表示了线性方程组中“真正起作用”的方程的个数，举例“滥竽充数”的故事，既提高了课堂的趣味性，又起到了育人的作用。