深入探究一道数学建模题中隐藏的核心素养

广东 雷雄军

《普通高中数学课程标准(2017年版2020年修订)》(以下简称为“课程标准”)提出通过高中数学课程的学习，学习能够发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等六大数学核心素养.发展学生的数学核心素养不仅要以课本的新课为载体，也要以课后的习题作业为载体.这就要求数学教师不仅要精选题目，还要在题目的使用过程中能够对题目进行灵活处理，激活题目，使得隐藏在题目背后的核心素养跃然纸上.本文笔者结合在一次精选试题时发现的一道难题(以下简称为“原题”)，在讲解过程中通过灵活的教学处理对题目所渗透的核心素养进行了深入的挖掘.

一、原题呈现

如图1所示为一种魔豆吊灯，图2为该吊灯的框架结构图，由正六棱锥O1-ABCDEF和O2-ABCDEF构成，两个棱锥的侧棱长均相等.且棱锥底面外接圆的直径为1 600 mm，底面中心为O，通过连接线及吸盘固定在天花板上，使棱锥的底面呈现水平状态，下顶点O2与天花板的距离为1 300 mm，所有的连接线都用特殊的金属条制成，设金属条的总长为y.

图1

(1)设∠O1AO=θ(rad)，将y表示成θ的函数关系式，并写出θ的范围；

(2)请你设计θ，当角θ正弦值的大小是多少时，金属条总长y最小.

此题对学生来说是一道难题，题目中蕴含了丰富的数学学科核心素养，但核心素养是蕴藏在题目里面的，需要我们通过恰当的教学设计去深入挖掘.在教学过程中，笔者对这道题的教学进行了灵活处理，通过灵活处理将隐藏的核心素养逐一挖掘出来.此道题的讲解虽然花了整整一节课，但是学生的收获也是满满的.

二、数学建模素养的渗透

课程标准给出数学建模是指对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养.数学建模搭建了数学与外部世界联系的桥梁，是数学应用的重要形式.其过程主要包括：在实际情境中从数学的视角发现问题、提出问题、分析问题、确定参数、建立模型、计算求解、检验结果、改进模型，最终解决实际问题.在平常我们复习做题过程中，问题基本上都是现成的，不需要学生去发现和提出.因此在做题过程中很难培养学生发现和提出问题甚至选择合适参数的能力.在上面的这个题目中，问题的背景是我们熟悉的现实情境——现实生活中魔豆吊灯.在这个熟悉的情境下，提出两个问题：

问题一为数学问题：设∠O1AO=θ(rad)，将y表示成θ的函数关系式，并写出θ的范围；

问题二为现实问题：请你设计θ，当角θ正弦值的大小是多少时，金属条总长y最小.

认真分析，这两个问题的实质就是一个问题，即什么情况下，金属条总长最小.第一问是为求解模型引入的参数相关问题.题目中问题如何提出的和参数如何确定的都已经直接呈现了，学生缺失了思考的过程.笔者在讲解这个题目过程中进行了适当的处理，让缺失的过程重新拾回.在给出题目后，没有直接给出题目中的两幅图，只给出了左边的实物图.

接下来，笔者提出第一个开放性问题：结合图象和题目中的条件，同学们可以提出什么问题？问题当然可以是数学问题，现实问题，也可以是科学问题.同桌之间互相讨论一下.在这个过程中，学生结合已经掌握的知识技能及生活经验，提出了一些问题.如金属条的承重问题，灯的功率问题，灯如何放置会更加美观，当然更多的是什么情况下金属条才能最短问题.在这一过程中可以培养学生用数学的语言表达现实世界，提高学生提出问题和分析问题的能力.这个过程恰恰是数学建模中的第一个过程，也是题目中无法呈现的.在同学们讨论结束后，笔者根据同学们提出的问题通过逐步分析确立要研究的数学问题：什么情况下，金属条总长最小.在确定问题后，笔者引导学生思考，要研究一个事物的变化，我们必须要引入参数，通过参数的求解才能确定事物的变化.接着笔者提出第二个开放性问题，原题中应该引入哪个量作为参数才能解决我们提出的问题.在这个过程中，教师引导学生在实际生活情境中，运用数学思维进行分析，发现情境中的数学关系.提高了从数学角度发现和提出问题的能力，提升了学生的数学建模核心素养.

三、直观想象素养的渗透

课程标准给出直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养.直观想象是发现和提出问题、分析和解决问题的重要手段，是探索和形成论证思路，进行数学推理、构建抽象的结构基础.主要包括：借助空间形式认识事物的位置关系、形态变化与运动规律；利用图形描述、分析数学问题；建立形与数的联系构建数学问题的直观模型，探索解决问题的思路.

原题中直接呈现了实物图的直观图形(图2)，笔者认为这样做不能很好地增强学生运用几何直观和空间想象思考问题的意识.因此，笔者在讲解过程中，在第一步结合实物图(图1)提出问题的基础上，没有直接给出原题中的几何图形(图2).而是让学生自己动手结合实物图画空间几何图形，并且把题目中的数量关系在几何图形中呈现出来，如下图.

学生通过抽象实物的几何直观图形，建立图形与实物的联系，体会图形与图形，图形与数量的关系.抽象出几何图形后，利用几何图形构建提出问题的直观模型，通过图形建立形与数的联系，进而理解问题的数学本质.金属条总长即是几何直观图中12O1A+6AB+O1P的值.结合几何的直观图形，笔者提出了开放性问题：引入什么量作为参数，能够构建原题的模型.学生比较多的是引入正六边形的侧棱长作为参数，设侧棱长为x，金属条总长

从而y=12O1A+6AB+O1P

由图形可知O1P=1 300-1 600tanθ>0，

1)独特的单线接口方式，DS18B20在与微处理器连接时仅需要一条口线即可实现微处理器与DS18B20的双向通讯；

至此，我们就解决了问题一.这个过程，我们主要是引入参数建立模型.教师要着重突出通过几何图形直观地描述和表达我们前面提出的问题，并且通过几何图形启迪学生解决问题的思路，让学生体会数形结合思想，提升学生直观想象核心素养.

四、数学运算核心素养的渗透

课程标准中给出数学运算是指在明晰对象的基础上，依据运算法则解决数学问题的素养.数学运算是解决数学问题的基本手段，主要包括：理解运算对象，掌握运算法则，探究运算思路，求得运算结果.

借助几何图形我们将现实问题建立成数学模型得出金属条总长关于∠O1AO=θ(rad)的函数关系式：

这个就是原题的运算对象，接下来是探索运算思路.求解函数最值方法有很多，最常用的有单调性法、基本不等式法和导数法等.通过对函数式子结构特征分析，发现很难使用单调性和基本不等式.因此，选择用导数性质解决.过程如下：

当θ∈(0,θ0)时，y′<0；当θ∈(θ0,φ)时，y′>0；

函数y=f(θ)的单调性与θ的关系列表如下：

θ(0,θ0)θ0(θ0,φ)f'(θ)-0+f(θ)↘极小值↗

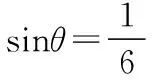
在整个运算过程中，学生除了掌握导数运算知识以外，还形成了求解最值的通性通法，并且根据问题的特征形成合适的运算思路.通过最终问题的解决，进一步提高学生的数学运算能力，通过运算促进学生数学思维的发展，形成规范化思考问题的品质.