基于认知逻辑链的三角函数单元教学策略分析
王世朋 汪煦 许晓天

摘 要:从结构编排、正文内容、例题与习题的角度对新、旧教材中三角函数单元的内容进行对比,分析不同点,并结合教学中的实际困惑,通过抓逻辑线索统领教学、用单位圆研究学习内容、用换元法分析典型例题和通过函数建模提升素养的单元教学策略,增强教学整体性和有效性.
关键词:认知逻辑链;单元教学;策略分析
三角函数单元是人教A版《普通高中教科书·数学》(以下统称“新教材”)必修第一册第五章的内容,在新教材中占有较大篇幅,在教学中用时也较多. 从教学实践来看,学生普遍感到内容多,难理清楚;公式多,难分准确;变形活,难选最优. 帮助学生和教师理清本单元的教学重点、难点及逻辑关系,助力教师系统地教和学生清楚地学是一件有意义的事.
一、问题提出的背景
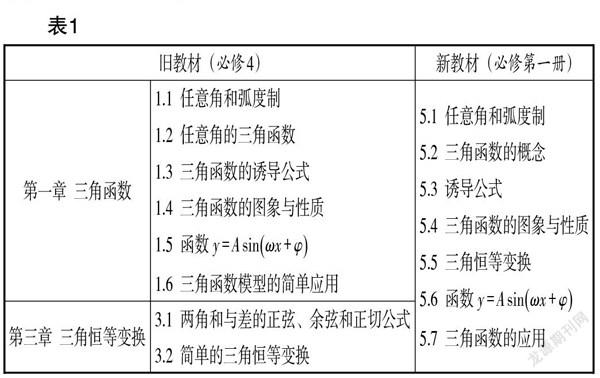
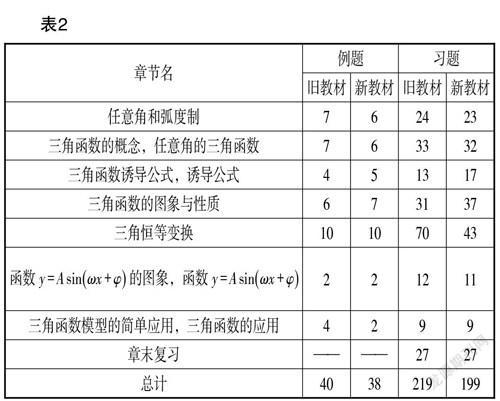
1. 新、旧教材的对比分析
以新教材与人教A版《普通高中课程标准实验教科书·数学》(以下统称“旧教材”)为研究对象,从结构编排、正文内容、例题与习题三个方面对三角函数内容进行比较分析.
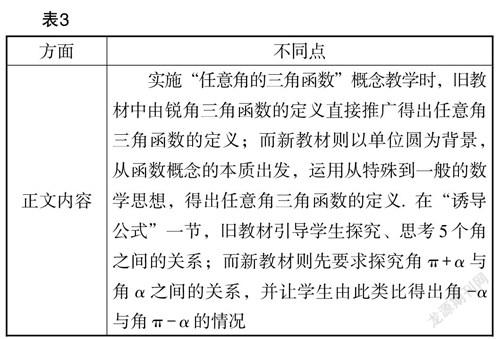
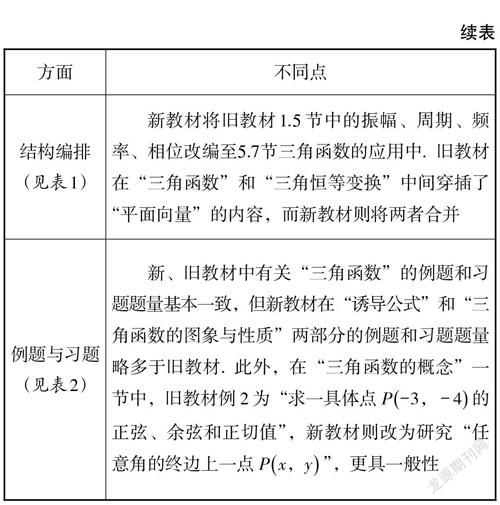
分析表1和表2的统计数据,可以得出不同点,如表3所示.
2. 教与学的困惑
(1)教师层面.
一方面,教师的观念尚未及时更新,不能准确理解新课程理念的变化,不能整体把握单元教学的系统性. 例如,概念、公式、图象和性质都可以由一个单位圆引出,与原来的知识体系相比,其整体性、逻辑性更强. 不再像旧教材中那样,要研究三角函数的图象先研究三角函数线,要获得两角差的余弦公式先学习向量知识. 理解好新教材,有助于理清知识脉络. 在教学实践中,很多教师依旧抱残守缺,不愿改变旧策略,照搬旧教法,因循守旧.
另一方面,部分教师试图接受新教材,却因为缺乏深度理解,最终只能流于形式,对于新教材中的很多探究活动选择直接略过. 例如,在弧度制的教学中,新教材意欲通过探究活动得出:圆心角[α]所对的弧长与半径的比值只与[α]的大小有关. 但是,在教学实践中,很多教师选择直接给出公式,并不注重说理过程. 在三角函数的概念教学中,新教材的探究目的是建立角[α]与终边的一一对应关系,进一步产生终边与单位圆的交点[P]的坐标的一一对应关系,让函数的引出显得自然. 听课中也明显感觉到,很多教师嫌烦琐,选择像旧教材那样直接根据锐角三角函数来进行定义.
(2)学生层面.
一方面,在初中,学生学习过利用锐角三角函数的定义解决直角三角形中有关的边角计算问题,缺少对三角函数的整体感知.
另一方面,学生不理解为什么三角函数是刻画周期函数的重要模型,对单位圆的引出感到困惑. 同时,对三角函数运算的内在联系认识不足,学习起来有一定困难. 另外,三角函数的学习内容中蕴涵许多思想方法,学生普遍感觉想不到、记不住、用不好.
二、学生认知基础分析
1. 知识与技能
在学习三角函数之前,学生已经学习了一次函数、二次函数、幂函数、指数函数和对数函数,对函数有了一定的认识. 三角函数是学生接触的第一个周期性函数,是高中阶段学习的最后一个基本初等函数.
在初中数学教学内容中,已有锐角三角函数的概念,但没有将其作为一种函数来学习,学生关注的只是三角函数值,主要利用锐角三角函数的定义解决直角三角形中有关边角的问题. 到了高中阶段,需要从函数的角度来认识三角函数.
2. 基本活动经验
学习三角函数的认知基础是函数的一般概念,以及对幂函数、指数函数和对数函数的研究经验,另外还有圆的相关知识. 然而,前面学习的基本初等函数涉及的量较少. 在三角函数内容中,对应关系不以“代数运算”为媒介,是“[α]与[x,y]直接对应”,实际上是几何元素间的对应,学生在已有的基本初等函数学习中没有这种认知,而且缺乏用联系的观点看问题的经验,致使对“如何发现函数的性质”认识不充分,最终难以自己总结出性质和概念,容易出现理解性偏差.
三、基于认知逻辑链的单元教学策略分析
教材是教与学的依据. 学生的数学认知逻辑链是以数学教材知识之间的逻辑结构为主线、以学生的数学认知基础为起点、以学生的数学思维为衔接形成的符合学生认知水平的逻辑关系. 一个单元就是一个思想体系、方法体系、知识体系. 要发展学生的数学学科核心素养,就应当着眼于知识结构的教学,这样才有利于素养的生成、发育和成长. 对于本单元,基于教材的变化、教与学的现状和学生的认知基础,有必要对教学策略进行总结与分析.
1. 以一条逻辑线索统领三角函数教学
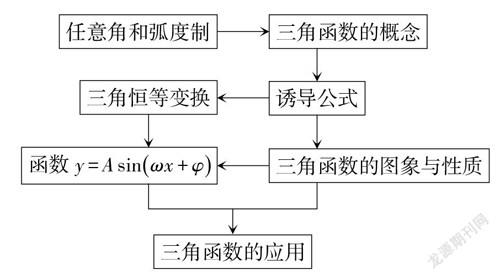
前面已经学习了函数的一般概念,并研究了指数函数、对数函数等,知道了函数的研究内容、过程与方法,以及如何用某类函数刻画相应现实问题的变化规律. 实际上,这些都告诉我们本章的学习思路为:概念→运算→函数的图象和性质→函数的应用. 知识结构如下图所示.
第5.1节可以理解为预备知识. 第5.2节完整学习三角函数的概念,进一步由定义产生三角函数之间的基本关系(第5.3节的诱导公式),再从定义和运算出发研究三角函数的图象与性质. 参照前面函数研究的基本套路,应该可以结束新知内容. 但是在实际生活中,由于三角函数模型常常具有一般性,需要采用从特殊到一般的研究策略,对诱导公式中涉及的特殊角与任意角[α]的和(或差)的三角函数进行一般化处理,变为任意角[α]与[β]的和(或差)的三角函数计算问题,由和角公式自然就会生成二倍角公式. 一方面,通过扩充把运算算理一般化,打通公式之间的逻辑关系;另一方面,为一般类型的三角函数图象和性质的研究提供算法保障. 然后,再进一步提出函数[y=Asinωx+φ]的图象和性质的研究. 基于换元法,函数[y=Asinωx+φ]的性質已经可以解决,自然引出:函数[y=Asinωx+φ]的图象能否通过变换由三角函数[y=sinx](或[y=cosx])得出?最后,再举例说明三角函数在科学与生活中的基本应用. 在知识学习中遵循循序渐进的原则,渗透了由特殊到一般的思想,体现了知识生成、发展与应用的完整过程.
2. 以一个单位圆引出三角函数的学习内容
三角函数是刻画周期性函数的重要模型,而圆周运动是一种常见的周期性变化现象. 要想用角的大小来刻画圆周运动,自然就需要扩大角的范围. 为了引出三角函数的概念,要用实数与角度一一对应,回到角度制定义的圆中研究. 不失一般性,选择单位圆进行弧度制的定义,为概念的学习做好铺垫. 再回到圆周运动中,可以比较清楚地把角与角的终边和单位圆交点的位置建立一一对应关系,提出三角函数的定义. 由三角函数的定义出发,直接可以获得诱导公式(一). 结合圆的几何性质,得到同角三角函数的基本关系公式. 进一步提出:如果从圆的对称性出发,能否研究三角函数的对称性?通过终边与单位圆的交点关于原点对称,获得诱导公式(二);通过终边与单位圆的交点关于[x]轴对称,得到誘导公式(三);通过终边与单位圆的交点关于[y]轴对称,得到诱导公式(四). 由此,实现了将任意角的三角函数转化为锐角三角函数.
前面,学习了同底指数函数和对数函数的图象关于直线[y=x]对称. 如果点关于直线[y=x]对称,可以得到诱导公式(五);如果点先关于直线[y=x]对称,再关于[y]轴对称,可得诱导公式(六). 沿着该线索,通过对描点法的改进,可以画出[y=sinx,x∈0,2π]的图象. 再结合单位圆上点的位置变化,可以研究周期性、奇偶性、单调性与最值. 正切函数的图象也可以结合几何性质,研究一个周期内的函数图象.
回到诱导公式中,能否把出现的特殊角扩充到一般角?能否建立两角和(或差)与两个角的直接联系?继续回到单位圆中,利用圆的旋转对称性进行推理. 在单位圆中,也可以结合旋转对称和关于直线[y=x]对称获得和差化积公式. 如果再追寻匀速圆周运动模型在生活中的应用,还可以提出用单位圆研究函数[y=][Asinωx+φ]中参数[φ,ω,A]对函数图象的影响.
用一个熟悉的单位圆,激起学生的认知冲突,引出角扩充的必要性;结合函数的概念提出弧度制的自然性;通过圆自身存在的对称性探究得到多维的运算公式;利用圆上点的稠密性和运动周期性研究函数的图象和性质;最后回归到生活情境中,体现数学知识的应用价值.
3. 以一种整体换元方法贯穿典型例题教学
在诱导公式的内容中,新教材第193页设置了例[5]. 注意到[53∘°-α+37∘°+α=90°∘],在计算中把[37∘°+α]视为一个整体进行处理,强化化未知为已知的基本策略.
在学习第5.4.2节正弦函数、余弦函数的性质时,对于新教材第201页的例2,在求函数的周期时,就采用了令[z=2x,z=12x-π6],目的是将问题转化为熟悉的研究函数[y=sinz]的周期的问题,起到化繁为简的作用,从而进一步提出一般性的探究问题和结论.
针对后续的单调性与最值的教学,新教材在第205页例3的第(2)小题和第206页的例5中都采用了整体换元法. 通过对不同类型问题的归一处理,提高学生的学习兴趣,有利于学生抓住求解问题的基本路径,将其内化为自己的学习能力. 在正切函数的图象与性质的学习中,新教材第212页的例6同样利用整体换元法研究了定义域、周期和单调区间. 在三角恒等变换的教学中,也非常注重强化整体换元法. 例如,利用[Cα-β]推导[Cα+β];新教材第221页的例5利用[4α=2 · 2α];新教材第222页的例6利用[2A+2B=2A+B];新教材第225页的例8第(2)小题令[α=θ+φ2,β=θ-φ2];等等. 这些都采用了整体换元法,突出已知和未知之间的关系,有利于直接建立联系,找到解题的突破口. 在新教材第237页的例1中,用“五点法”画出函数在一个周期内的图象,先令[X=3x-π6],目的是将问题转化为研究一个标准函数[y=sinX]的图象,从而使图象在一个周期内能完美呈现五个关键点,方便观察、研究函数的基本性质.
不难发现,对于三角函数问题,从运算到性质,新教材几乎都采用整体换元策略分析并解题,不断强化通法意识,让学生形成连续的思维方法,有利于实现教、学、评的一致性.
4. 以一类函数建模驱动素养教学
三角函数可以用来刻画现实世界中的许多变化与现象,如潮汐变化、物体做匀速圆周运动的位置变化、物体做简谐运动的位移变化、交变电流变化乃至月亮圆缺现象等. 新教材形象地呈现两个齿轮的旋转示意图,提出旋转方向不同,需要扩充角,也建构了扩充的基本线索:角度[+]旋转的方向.
在利用单位圆探究三角函数的基本运算和性质后,新教材回应了前面的章引言,用古代筒车作为数学模型来研究匀速圆周运动,通过提出问题、优化变量、分析模型,建立模型中盛水筒[M]距离水面的高度[H]与时间[t]的函数关系式[H=rsinωt+φ+h]. 利用函数[y=sinx]的性质研究方法,可以研究该模型的基本性质,提出“如何用变换的方法研究函数[y=Asinωx+φ]的图象”的问题. 通过展示现实生活中摩天轮的模型,引导学生明白如果做相似研究(游客距离地面的高度[H]关于转动时间[t]的关系),可以利用本章学习的知识进行探究. 在本章的最后一节中,研究了弹簧振子的震动问题、交变电流问题、沙漏摆动问题、日常温度变化问题、海水潮汐问题、人体节律变化问题、恒星亮度变化问题,以及地球公转中太阳直射点的维度变化问题.
整个章节的设计,很好地体现了数学教学要强化“三会”的教学方法. 从数学眼光开始,发现两个齿轮转动的角度不同,方向也不同. 紧接着,在单位圆中,提出如何刻画[α]与终边和单位圆交点[Px,y]中的坐标[x,y]之间的函数关系,引出三角函数问题. 运用数学思维思考问题,形成研究路线,产生三角函数的概念、运算和性质. 再用数学语言表达问题,如三角函数涉及具体概念、运算公式和基本性质. 最终帮助学生运用所学知识分析、探究和初步解决实际问题,提高学生分析问题和解决问题的能力,发展学生的数学学科核心素养.
四、关于三角函数单元教学的一点思考
单元教学的“单元”可大可小. 对于本章内容而言,可以以“三角函数”整章为单位进行大单元教学,也可以采用大背景、大观念、大任务引领下的小单元教学.
客观来说,为了增强可操作性,提高教学效果,可以分解为许多小单元进行教学,如以“三角函数的概念”“三角函数的诱导公式”“三角恒等变换”“三角函数的图象”“三角函数的性质”“三角函数的应用”等知识内容为主线开展单元教学;可以开展以方法为主题的单元教学,如“三角函数中的整体换元方法”“基于单位圆的三角运算”“利用单位圆研究三角函数性质”等;可以开展以数学思想或核心素养为主线的单元教学,如“转化与化归思想在三角函数中的应用”“数学建模素养在三角函数中的应用”“逻辑推理素养在三角公式证明中的运用”等;可以围绕典型问题开展以探究活动为教学形式的单元教学,如“三角函数的单调性研究”“基于变换的函数[y=Asinωx+φ+B]的图象探究”等. 选择什么样的主题开展单元教学,需要依据学情和实际教学进展有计划地组织,真正服务于学生的学习和成长,实现高效地教与学.
参考文献:
[1]刘存华,岑盛锋,周莹. 课程标准视域下的高中数学新旧教材比较分析:以“三角函数”章节为例[J]. 中学数学研究,2020(6):8-11.
[2]许晓天. 构建学生数学认知逻辑链下的教学设计:由一节优质观摩课想到的[J]. 中学数学教学参考(上旬),2020(7):25-27.
[3]喻平. 数学单元结构教学的四种模式[J]. 数学通报,2020,59(5):1-8,15.
[4]李昌官. 高中数学研究型单元教学实践探索:以“三角函数的诱导公式”教学为例[J]. 中国数学教育(高中版),2020(1 / 2):16-21.

