n级时间球πn的统一公式
李玉发 李宇航
(1.广东省惠州市第一中学 516001;2.澳大利亚国立大学)
一、基本原理
听了张景中院士报告《点如何相加》,以及扬学枝教师对点量的研究,深受启发,在点方程、线方程、面方程和体方程等方面得到了自己的一些想法.
为弄清点量,我们提出时点、零点、光点的相关定义:
定义1n维的时点Pn=(x0,x1,…,xn-1)(n∈N+,xk∈R,k∈N),P0=(x0)=x0.
定义2 零点On:O0=Φ,O1=(0),O2=(0,0),O3=(0,O2),…,On=(0,On-1).
定义3 数光点Tn:T1=(1),T2=(0,1),T3=(0,0,1),…,Tn=(On-1,1).
形光点Jn:J0=(1),J1=(0,1),J2=(0,0,1),…,Jn-1=(On-1,1).
有结论:Tn+1=Jn(n∈N).
为了使不同维度的点能加减,我们提出升维、加减的相关定义:
定义4 升维:(k∈N,n∈N+,xk∈R)
(1)x0=(x0)=(x0,0)=(x0,02)=(x0,0n).
(2)(x0,x1)=(x0,x1,0)=(x0,x1,02)=(x1,x2,0n).
(3)(x0,x1,…,xk)=(x0,x1,…,xk,0)=(x0,x1,…,xk,0n).
定义5AB=B-A;OB=B.
定义6 关于形时空间Jn与数时空间Tn,有(0)J0={(x0)|x0∈R}=T1=R(称为0维点时空或1元数时空);
(1)J1={(x0,x1)|x0,x1∈R}=T2(称为1维线形时空或2元数空间或复平面时空);
(2)J2={(x0,x1,x2)|xn∈R,n∈N}=T3=R3(称为2维面形时空或3元数时空);
(3)J3={(x0,x1,x2,x3)|xn∈R,n∈N}=T4=R4(称为3维体形时空或4元数时空);
(4)J4={(x0,x1,x2,x3,x4)|xn∈R,n∈N}=T5(称为4维形时空或5元数时空);
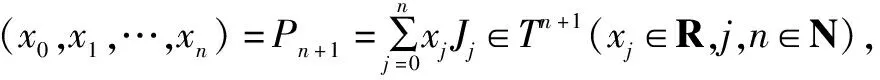
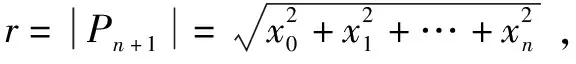

(2)零点On的模|On|=0;
(3)若|Pn+1|=1,称点Pn为单位点,记Pn+1=En;
(4)光点Tn是单位点,Tn的模|Tn|=1;
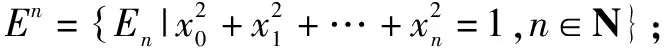
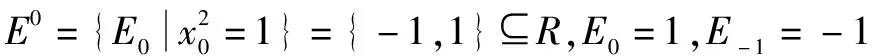
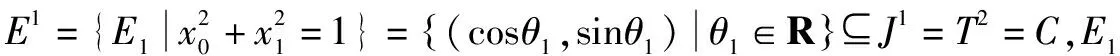
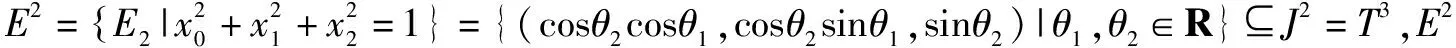
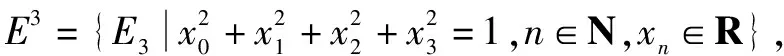
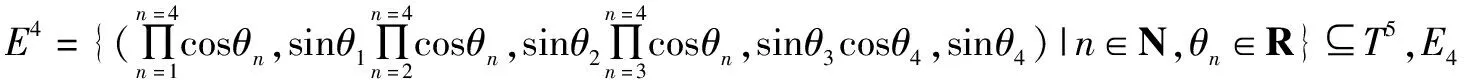
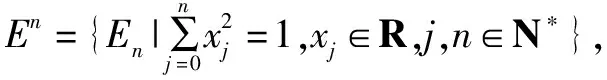
二、主要结论
结论1Pn=(x1,…,xn),(xk∈R,k,n∈N,n≤5),Tn={Pn|n∈N*},半径为r的球形Pn=rEn-1的模空间Mn(r)测度记为Dn-1(r),则
(2)点线可加:(D0+D0)r=D1(r),
(D1(r)+D1(r))r=D2(r);
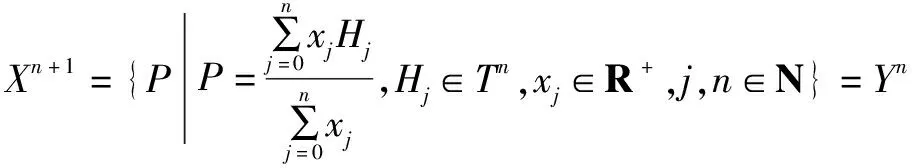
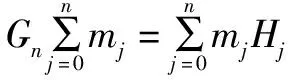
结论4 由J0={(x0)|x0∈R}=R1=T1得一维实点就是实数,一般可得:Jn=Rn+1=Tn+1.
结论5n维球形空间En(直形空间Xn,椭形Sn(a0,a1,…,a2))的测度记为Dn,有维度公式:同一数时空间的维度=同一形时空的维度+1,即Jn={(x0,x1,…,xn)|xn∈R,n∈N}=Tn+1=Rn+1.
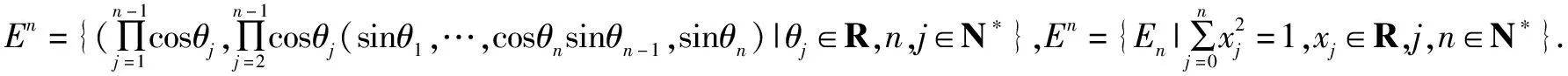
为了让二维以上点量既能加减又能乘除,定义旋转点.
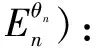
Wn={Wn|En+1=(cosθn+1)En+(sinθn+1)Jn+1(n∈N*),E1=T1=1,T2=i,i2=-1},
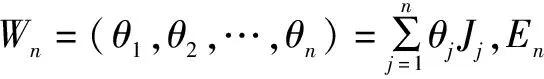
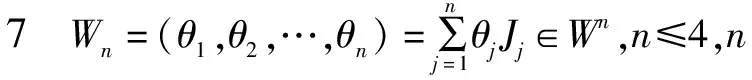
eWn=eWn-1cosθn+Jnsinθn(n∈N*),θ0=0,T2=i,T0=-1,
(D4n,D4n+1,D4n+2,D4n+3,D4n+4)=(点,线,面,体,新时点),n∈N.
三、具体应用
由结论7可推出下面一些结论:
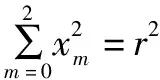
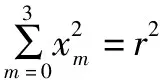
由结论1与结论7可推出下面一些结论:
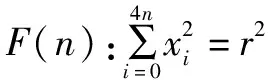
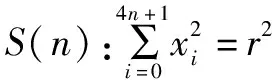
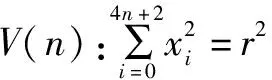
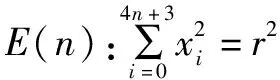
证明n=0或n=1时,可验证(A)成立,即
假设n=k,(A)成立,有
n=k+1时,
由结论1与结论7,两点相加得线,两线相加得面,面积分得体,体积分得时间(点),即
(D4(k+1)(r)+D4(k+1)(r))r=(πk+1r4k+4+πk+1r4k+4)r=2πk+1r4k+5=D4k+5(r),
(D4k+5(r)+D4k+5(r))r=(2πk+1r4k+5+2πk+1r4k+5)r=4πk+1r4k+6=D4k+6(r),
=πk+2r4k+8=D4k+8(r),
综上,(A)对一切n∈N都成立.
点评深刻准确地理解、挖掘、建立数学中的数与形的关系,并恰当、巧妙地进行转换是数学学习与研究的基本功之一.
例1(2014年广东理科第9题)求不等式|x-1|+|x-2|≥5的解集.
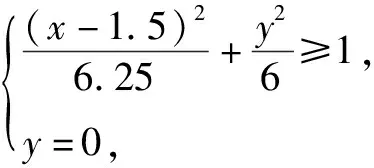
点评把一元不等式转换为二元不等式组,比较难求一维的边界点P1(-1),P2(4)升维转换为易求的椭圆边界曲线的顶点A1(-1,0),A2(4,0).
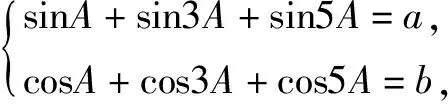
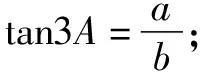
(2)(1+2cos2A)2=a2+b2.
分析设z=cosA+isinA,w=b+ai=z+z3+z5,有w=z3(z-2+1+z2),而k=(z-2+1+z2)∈R,w是z3的实数倍,所以w=kz3(k∈R).
即(cosA+cos3A+cos5A)+i(sinA+sin3A+sin5A)=k(cos3A+isin3A).
所以w=b+ai=k(cos3A+isin3A).
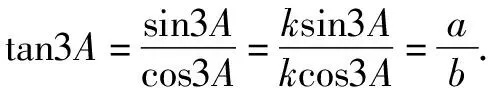
由模的公式对|w|2展开,得(1+2cos2A)2=a2+b2.
点评本题有多种证法,可以从不同的角度去思考,去探索,可以从三角、几何、复数等不同方面去思考,只要我们努力去挖掘其隐含的意义,何愁难关不破!

