一类抽象函数解析式求法的反思
李昌成
(新疆乌鲁木齐市第八中学 830002)
抽象函数在现行教材中没有介绍,但是有关抽象函数的题目在各类教辅资料中屡见不鲜,尤其是“已知f(ax+b)=g(x),求f(x)”的试题在全国各地的高考卷中层出不穷.在教学中发现学生普遍掌握得不好,存在生搬硬套的现象,难以达到举一反三的水平.由此引发了我对此类问题的研究,通过探究这类问题的本质,发现“已知f(ax+b)=g(x),求f(x)”的问题至少有5种解法.
一、概念说明
所谓复合函数是指形如y=f(h(x))的函数,其中u=h(x)叫做内层函数,y=f(u)叫做外层函数.复合函数的一个基本原理:内层函数的值域是外层函数的定义域.
二、解法探究
解法1 (定义法)因为f作用的对象是ax+b,于是我们可以将条件左端g(x)等价变形为关于以“ax+b”为运算对象的关系式.进而求得f(x).
例1 已知f(x+1)=x2+x-1,求f(x).
解析由于f(x+1)=x2+x-1=(x+1)2-2x-1+x-1=(x+1)2-(x+1)+1-1-1=(x+1)2-(x+1)-1.
由于x与x+1的取值范围相同,所以f(x)=x2-x-1.
评析这种解法要求学生思路清晰,运算目标明确,还要有一定的运算能力,否则难以实现目标,一般按照次数逐项拼凑,这种方法又称拼凑法.
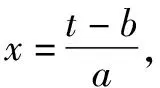
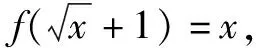
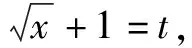
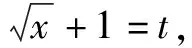
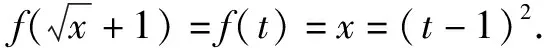
①
于是f(t)=(t-1)2.
②
所以f(x)=(x-1)2(x≥1).
③
评析在①处学生容易绕不清,每一个等号的来历不理解;③处的定义域初学者容易忘记,也弄不清;③处的x与②处的t是同一个变量,只是记号与习惯而已,体现了内层函数的值域是外层函数的定义域.
解法3 (赋值法)在集合思想的引导下,通过对复合函数的内层函数u=ax+b进行适当地赋值,使得内层函数转化为最简形式u=x,从而求得f(x).
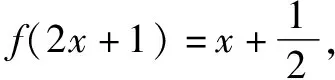
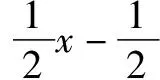
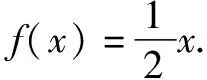
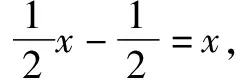
解法4 (待定系数法)若g(x)为一次函数,且内层函数是u=f(x),此时f(ax+b)=g(x)变形为f(f(x))=g(x),可以推证f(x)为一次函数(*),进而可以通过待定系数法确定f(x)的斜率和纵截距.下面证明(*).
设f(x)=kx+b,那么f(f(x))=kf(x)+b=k(kx+b)+b=k2x+(kb+b).
因此,当g(x)为一次函数时,f(x)一定为一次函数.
比较系数可得关于k,b的方程组.
例4已知f(f(x))=4x+3,求f(x)的解析式.
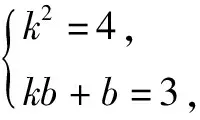
评析这种解法适用于已知函数类型的题目.本质是建立相关参数的方程组,通过解方程组完成解答.
解法5 (平移法)当u=ax+b中的a=1时,由于y=f(x+b)是由y=f(x)平移而得,所以可以通过平移法则求解f(x).
例5 已知f(x-1)=x2+x,求f(x).
解析y=f(x-1)是由y=f(x)向右平移1个单位而得,由逆向思维得y=f(x-1)向左平移1个单位就是y=f(x).
所以f(x)=f((x+1)-1)=(x+1)2+(x+1)=x2+3x+2.
评析这种解法适用于u=ax+b中的a=1的情形,将图象平移与代数运算有机结合起来,从另外一种角度认识了抽象函数,有利于对抽象函数的理解.
三、教学反思
从以上几例可以发现,这类问题学生之所以掌握得不太好,是因为解法因题而异,必须根据题设灵活选择解题方法,尤其是定义域的处理变化多端,实质是求内层函数的值域.学生对此的理解是一个螺旋上升的过程,我们要遵循高一学生的认知规律,扎实有效地推进教学.
1.适度拓展,单元整体设计,理顺知识间的逻辑
《函数及其表示》一节主要介绍了函数概念和表示方法,其中还牵涉函数的定义域、值域、同一函数等概念.为了提高学生对函数概念的理解,我们有必要对定义域、值域、函数解析式求法进行拓展教学,否则学生难以适应后续的教学,也达不到高中数学教学要求.
对于定义域,一般常见的函数定义域问题学生均可以借助集合的知识完成,但是对于抽象(复合)函数的定义域学生非常迷茫,我们有必要介绍复合函数.首先要理解复合函数的概念,其次要理清内层函数、外层函数,再次要灵活应用“内层函数的值域是外层函数的定义域”解题.否则,学生难以应对以下三类定义域问题:已知外层函数f(x)的定义域,求复合函数f(g(x))的定义域;已知复合函数f(g(x))的定义域,求外层函数f(x)的定义域;已知复合函数f(g(x))的定义域,求另一复合函数f(h(x))的定义域.
对于值域,教材仅介绍了概念和简单例题.事实上,值域是一个复杂问题,随着学生知识面的扩大,难度越来越大.若处理不到位,抽象函数的定义域经常出错.
抽象函数解析式是本节的难点,解题方法多,诸如定义法、换元法、拼凑法,待定系数法、函数方程组法、特值法,并且应用灵活.在教学中应当做到单元整体设计、整体推进,知识融合,前后照应才能产生良好的教学效果.
2.开展深度教学,使学生把握问题本质
复合函数问题在教材上未有涉及,但是高考中时常出现.因为这是一个拔高的要求,能考查学生的数学思维品质.众所周知,把问题一般化才能深入理解问题.深度教学的发生离不开教学的组织与引导,我们必须克服教学过程中表面、表层、表演的局限,引导学生深层、深刻、深度学习.经历从理论到实践的一整套思维过程和行为模式的转化,深度教学才能促进深度学习真实发生.
3.充分调动学生积极性,落实实践教学
实践教学尤为重要,讲一讲,做一做,变式训练及时跟上.抓住高一新生善于表现的特征,可以开展现场限时解题比赛,既能提高速度,又能增大课堂容量.学生现场板书必不可少,小组合作突破难点,同伴互助找到自己认识上的误区,不能搞老师一言堂.让学生点评是提高全体学生思维的好办法,同龄人思维接近,看待问题相近,纠正一题就提升一片.何乐而不为呢?
4.遵循教学规律,递进式推进教学
问题之所以困难,是因为有的学生理解不到位,老师推进太快.我们要遵循教学规律,先教会内层函数值域为R的,再给出内层函数值域非R的;最后再介绍几何法(平移);然后将内层函数复杂化,值域非R,有一定计算量的.递进式教学符合学生的认知特征,让问题越来越深刻,学生就真正掌握问题了.

