溯本求源·发展素养
——对几何体外接球问题的思考

◎史彬彬

(南宁市东盟中学，广西 南宁 530105)

空间几何体外接球球心位置的确定是解决立体几何问题的重点和难点，要求学生具有较好的空间想象能力，并能熟练掌握空间几何体的结构特征及位置关系的判断方法，这也是发展学生直观想象和逻辑推理两个学科核心素养的重要载体.笔者从球截面的几何性质和代数特征出发，通过对圆柱、圆锥的外接球球心位置的确定及半径的计算，对多面体的外接球问题进行思考.

一、球截面的性质

几何性质平面与球相交，交线为圆，且球心与截面圆圆心所在的直线垂直于截面.

代数特征如图1，球心为O，截面圆圆心为O′，则直线OO′⊥圆O′.设球O的半径为R，圆O′的半径为r，|OO′|=d，则由勾股定理得R，r，d满足R2=r2+d2.

图1

二、圆柱的外接球

问题1记圆柱的高为h，底面圆的半径为r，求该圆柱的外接球半径R.

图2

例1(2017年·全国卷Ⅲ)已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球面上，求该圆柱的体积.

延伸1.1如图3，以圆柱底面圆的任意内接多边形为底面，该多边形的顶点对应的母线为侧棱的直棱柱的外接球与该圆柱的外接球相同.

图3

例2(2010年·课标卷)设三棱柱的侧棱垂直于底面，棱长都为a，求该三棱柱外接球的表面积.

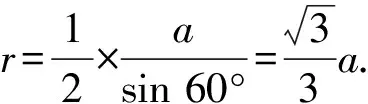
延伸1.2侧棱垂直于底面，且底面多边形存在外接圆的棱锥可补形为圆柱，该棱锥的外接球与对应圆柱的外接球相同.

例3(2021届西南名校高三第三次联考)如图4,已知三棱锥P-ABC中，∠BAC=90°，∠APC=30°，平面PAC⊥平面ABC，AB=AC=4，求三棱锥P-ABC外接球的表面积.

图4

三、长方体的外接球

问题2记长方体的长、宽、高分别为a，b，c，求该长方体外接球的半径.

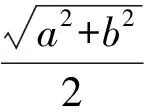
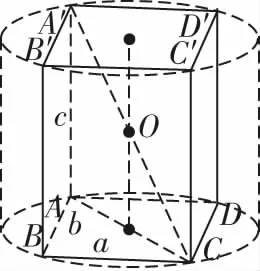
图5

例4(2017年·全国卷Ⅱ)长方体的长、宽、高分别为3，2，1，其顶点都在球O的球面上，求球O的表面积.

解析设球O的半径为R，则(2R)2=32+22+12=14，故表面积为14π.

延伸在长方体的八个顶点中，选取不共面的四个顶点构成一个三棱锥，则该三棱锥的外接球与长方体的外接球相同.

根据不同的取点方法，可以得到如下两类三棱锥：①侧棱垂直于底面，且底面是直角三角形的三棱锥，如图6(1)(2)；②对棱长相等的三棱锥，如图6(4).对于图6(3)，△ABP与△ACP均是以AP为斜边的直角三角形，则AP的中点到A,B,C,P的距离相等，由球的定义知AP为球的直径.

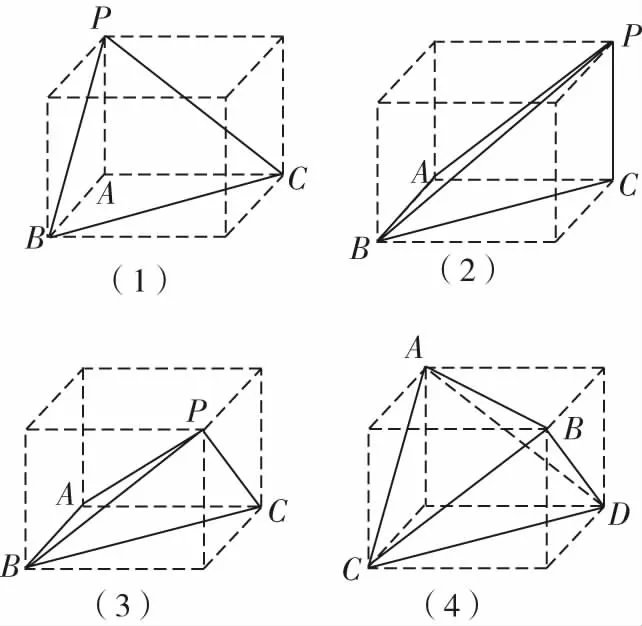
图6

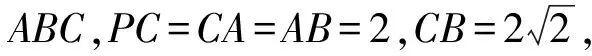
解析因为AC2+AB2=BC2，所以△ABC为以BC为斜边的直角三角形.又因为PC⊥平面ABC，所以可补形为如图6(2)所示的长方体.由题设知长、宽、高分别为2，2，2，所以外接球半径R满足(2R)2=22+22+22，即4R2=12，则表面积为12π.

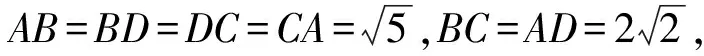
则a2+b2+c2=9，故外接球的表面积为4πR2=π(a2+b2+c2)=9π.

注长方体是特殊的直棱柱，其外接球问题可以利用圆柱模型求解.讨论长方体的外接球源于两方面的思考：(1)长方体是学生最先学习且最为熟悉的空间几何体，是学生认识立体几何中位置关系的重要载体.对长方体外接球球心位置的讨论，有助于学生理解其他几何体的外接球问题.(2)对棱长相等的三棱锥，不易补形成圆柱.

四、圆锥的外接球

问题3记圆锥的高为h，底面圆的半径为r，求该圆锥外接球的半径.

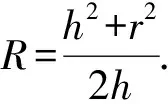
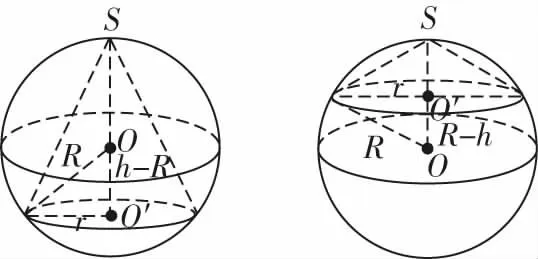
图7

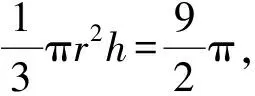
延伸如图8，以圆锥底面圆的任意内接多边形为底面，圆锥的顶点为顶点的棱锥的外接球与该圆锥的外接球相同.即顶点在底面内的射影为底面外接圆圆心的棱锥(侧棱长相等)可补形为圆锥.

图8

例8(2014年·全国卷)若正四棱锥的高为4，底面边长为2，求该棱锥外接球的表面积.

五、一般多面体的外接球

对于一般多面体的外接球问题，可以考虑以下解决办法：

思路1考虑多面体不在同一平面内的部分顶点，将问题转化为长方体或旋转体的外接球问题.

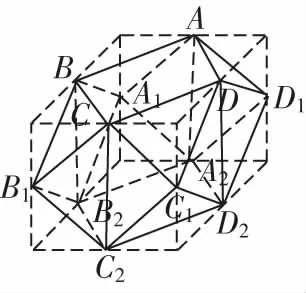
图9

思路2类比三角形外接圆圆心位置的确定方法，确定多面体外接球的球心.

因为球心在过截面圆圆心且垂直于截面的直线上，分别过多面体相交的两个侧面的外心作平面的垂线，那么两条垂线的交点就是该多面体外接球的球心，交点到任意顶点的距离为半径.

例10如图10，在边长为4的等边三角形ABC中，D，E分别为AB，AC的中点，将△ADE沿DE折起，使得平面ADE⊥平面BDEC，求折叠后所得四棱锥A-BDEC的外接球的表面积.

图10

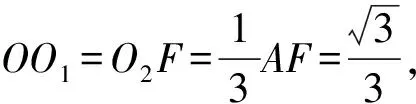
一般结论如图11(1)，记△ABC的外心为O1，△PAB的外心为O2，过O1,O2分别作平面ABC、平面PAB的垂线m,n，则直线m,n的交点即为外接球的球心O.取AB的中点为D，则O1D⊥AB,O2D⊥AB，设∠O1DO2=θ(θ为二面角P-AB-C所成平面角的大小).

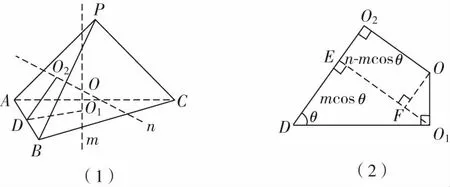
图11

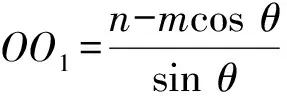
六、归纳总结

空间中，不在同一平面内的四点确定一个球.若一个多面体存在外接球，则只需在多面体的顶点中合理地选择不在同一个平面内的四点，那么这四点所对应的外接球就是该多面体的外接球.故解决三棱锥的外接球问题是关键.

对于一般的三棱锥，结合题设中所给的结构特征(如面面垂直)，类比三角形的外接圆，利用两个面的“中垂线”确定球心，将立体几何问题转化为平面几何问题求解即可.

七、教学建议

多面体外接球球心的确定因结构特征的不同，解决方法也不同，但其本质都是球截面性质的应用.

在教学过程中，教师可借助信息技术手段，通过“截面的性质与弦的性质、圆柱的外接球与长方形的外接圆、圆锥的外接球与等腰三角形的外接圆、三棱锥的外接球与三角形的外接圆”的类比，动态地展示平面图形向空间图形的转化过程，引导学生在圆柱、圆锥两个旋转体外接球的基础上对多面体的外接球进行思考，以小见大，深入挖掘，体现转化与化归的数学思想方法，培养学生从源头上分析问题和解决问题的能力，促进学生直观想象和逻辑推理等核心素养的发展.