基于核心素养培养的初中数学概念教学初探

许文厂

［摘  要］ 概念是数学的核心. 概念教学是渗透数学思想，落实数学核心素养的关键. 重视概念教学，不仅能培养学生用发展的眼光看待世界，还能让学生学会用数学语言和思维表达和思考生活. 文章以概念形成的一般过程为出发点，从问题驱动，孕育新知；归纳类比，形成概念；挖掘内涵，深化概念三方面具体谈谈基于核心素养培养的初中数学概念教学的措施.

［关键词］ 核心素养；概念教学；问题驱动

概念是数学中最基本的抽象，是培养学生思维品质、创新意识与应用能力的基础. 新课标中对数学核心素养所提出的要素是数学抽象、推理、建模、想象、运算与数据分析等. 数学概念的教学是促使学生形成良好核心素养的根本. 如何让学生在概念的形成与发展过程中，感知其内涵与外延，形成良好的核心素养，是笔者近两年一直在探索的问题之一. 文章从以下几方面，具体谈谈基于核心素养培养的初中数学概念教学方法，与同行分析交流.

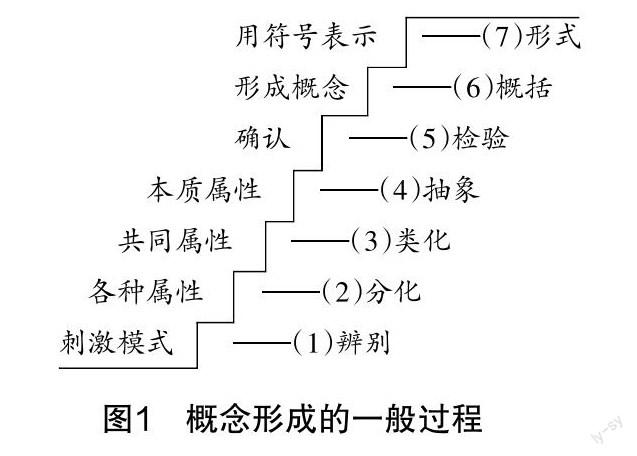
概念形成的一般过程

概念形成是发展学生数学核心素养的重要载体. 课堂教学中，怎样从情境中抽象出相应的概念是教学的重点与难点. 为此，笔者对概念形成的一般过程做了一定的研究，以期为教学服务.

杜宾斯基等人在APOS理论中提出，学习者在经历概念抽象的过程中，会经历操作、过程、对象与图式四个阶段. 奥苏贝尔（D.P.Ausubel）认为概念的形成与发展大致需经历八个阶段的心理历程. 结合以上理论，我国的学者章建跃与曹才翰共同提出了概念形成的一般过程，需经历七个阶段（见图1）［1］.

此理论对于一般意义上的概念教学具有明确的指导意义. 但教学是一个动态的过程，具有一定的复杂性与灵活性，尤其受一些概念的特征与学生认知水平的影响，教学实施过程中，难免会出现不遵循以上线性发展顺序的情况. 那么，教师在教学中应怎样地引导学生的思维，帮助学生构建清晰的概念，促进其核心素养的提升呢？这是一个值得教师深入探讨的问题.

培养策略

1. 问题驱动，孕育新知

传统教学模式中，教师习惯用“传授”的方式进行教学，学生按照教师的指令进行学习. 这种模式下，学生一般不会主动对教学过程或内容产生疑问，也不会主动去探索新知，而是被动地接纳. 显然，这种教学模式禁锢了学生的思维，让学生养成被动学习的习惯，从而缺乏学习的主动性.

随着新课改的推进，“以学生为主体”的课堂模式登上教育的舞台，明确了学生在课堂教学中的主体地位. 如何化被动为主动，让学生积极主动地参与教学活动呢？实践证明，丰富的情境能有效地激发学生的探究热情；具体的问题，能启发学生的思维；良好的课堂氛围，能激发学生的潜能. 学生在和谐、民主、自由的课堂中自主合作探究，不仅能充分张扬学生的个性，还能有效地激发创新意识，为数学核心素养的形成奠定基础.

案例1  “数轴”的教学

本节课的教学重点与难点在于数轴的建模及有理数与数轴一一对应关系的教导. 照本宣科地进行填鸭式教学，只会让学生处于云里雾里的状态，无法弄清概念的本质，更谈不上对概念的深刻理解. 而创设问题情境，驱动学生的思维，是实施课堂导入的关键. 在设计问题情境之前，教师首先要思考：数轴教学的目的、作用以及生活意义是什么？只有弄清了这些问题，才能从真正意义上引导好学生.

基于以上思考，笔者在本节课教学时，创设了以下问题情境.

羽毛球馆在学校大门东侧40 m处，图书馆在羽毛球馆东40 m处，小明从学校大门出发，先往西走了110 m，又折回来往东走了320 m，求小明在图书馆的什么位置？

这是一个与学生生活密切相关的问题，很快就吸引了学生的注意力，还没等教师提出要求，不少学生已经在草稿纸上圈圈画画，进行探究了.

巡视过程中，笔者发现学生的思维非常活跃，各种表达方法都有，大部分学生选择的是用线段图来表示. 为了让学生有一个明确的研究方向，教师可鼓勵学生先自主描述这个问题情境，然后统一要求学生在自己所画的线上取一点为0点，而涉及的一些数据，则可用直线上的点来表示.

通过不断地交流与修正，学生的意见逐渐趋于统一：以学校为0点，学校往东作为正数方向，学校往西作为负数方向，并选择一个标准长度为单位. 如此，在这个问题情境的驱动下，数轴的三要素已初见端倪. 学生在此探究过程中，不仅表现出了良好的主动思考、探究的能力，还对数轴的学习产生了良好的情感倾向.

2. 归纳类比，形成概念

有些数学概念相对抽象，学生学习起来有一定难度. 但仔细分析，会发现知识之间存在一些关联性，根据这个特征，将学生认知结构中的旧知与新知进行类比教学，往往能实现知识由此及彼的迁移，达到良好的教学效果.

初中阶段涉及的概念较多，如函数、不等式等，虽然类型繁多，但知识之间确实存在一定的联系，抓住这些联系就为教学提供了类比的条件. 从学生已有的认知结构出发，通过类比的方式，将已知迁移到未知的领域中，并类比分析、归纳总结，即可突出重点，突破难点，提高教学成效.

类比是一种重要的数学思想方法，除了在概念教学中应用得较多，在解题中也有大量使用. 因此，教师应从思想上重视这种方法的应用，并从行动上加强对这种方法的探究. 值得注意的是，教师应从思维上形成一个认识：类比就是类比推理，它是知识的迁移过程，而非两个或两类知识的差异性比较.

案例2  “反比例函数”的概念教学

在课堂导入环节后，笔者特设计了以下几个问题，让学生进行类比推理与概括.

问题1：观察以下四个表达式，y=，y=7a+20，y=3.8n，t=，并思考以下问题.

（1）以上四个表达式中，分别有几个变量？

（2）每个式子中的变量之间有没有关系？若有，说一说其中的联系.

（3）我们一般应用哪些模型来研究变量间的关系？

（4）你们对这些函数熟悉吗？

（5）能否为不熟悉的函数起个名字？

设计意图  循序渐进的问题串，让学生对函数产生更为直观、深刻的认识，学生通过一次函数与正比例函数的回顾，再次体会函数之间的对应关系，从而将这种关系迁移到反比例函数中. 随着认知矛盾的产生，学生自然而然地产生了进一步探究的想法，随着新旧知识的类比概括，学生对反比例函数的概念产生了初步的认识.

问题2：大家回忆一下，当初研究一次函数的时候，是从哪些方面着手进行分析的？如果要研究反比例函数，该从何处着手呢？

问题3：观察问题1中所提供的反比例函数解析式，它们之间存在哪些异同点？（分组合作）

问题4：通过以上的类比与总结，大家对反比例函数的解析式所具备的公共特征已有所了解，现在请大家根据正比例函数的定义，推导出反比例函数的定义.

随着以上问题的逐个击破，学生获得反比例函数的定义为：形如y=（k≠0，且为常数）的函数. 教师强调：x为自变量，y为x的函数，k为反比例系数.

任何一种函数思想方法的研究，首先是概念的研究，让学生对概念的图象与性质产生清晰的认识后，再学会运用概念来解决相应的问题［2］. 以问题引导与类比归纳的方法，意在帮助学生将旧知的学习方式进行加工，迁移到新知的学习中. 同时，类比、归纳思想的应用，使得学生大概了解了研究函数问题的通用方法，为今后研究其他函数做铺垫.

根据本例可知，紧扣知识内部联系，不仅能顺利实现知识的迁移，还能有效地发展学生的思维，让学生通过一个问题的研究获得解决一类问题的能力. 因此，类比归纳，获得概念的过程是概念教学的关键，也是培养学生形成良好学习能力的基础，更是促进学生核心素养形成的基本条件.

3. 揭示内涵，深化概念

在学生对概念有了明确的认识后，接下来的教学任务就是揭示概念的内涵与外延，让学生全方位地认识与理解概念，为概念的灵活应用奠定基础. 如何揭示概念的内涵，这是广大教育者一直探索的问题，也是令不少教师感到困惑与棘手的问题之一. 为此，笔者针对这个教学环节做过多方面的尝试. 实践证明，引导学生动手操作、引用概念的发展史、多角度分析概念等方法是揭示概念内涵的有效措施.

案例3  “无理数”的教学

为了揭示无理数的内涵，让学生感知无理数的特征，笔者特以认识为例，引导学生感知揭示概念内涵的过程，以深化学生对无理数概念的理解.

分析：纵观的形成与发展历史过程，在很早之前就出现了的近似值，但较晚才证明它无法用分数的形式来表达. 从认知发展规律的角度分析，初中阶段学生从已有的生活经验出发，能对有理数产生比较合理的认识，但对无理数的认识却处于一个模糊的状态. 结合学生的认知特点，教授有理数与无理数的区别时，教师可引导学生从近似值的角度出发，感知其无限不循环的小数特征，而非通过逻辑证明的方式来理解.

问题1：一个边长为x的正方形，它的面积为x2. 若x的值为1，那么该正方形的面积为x2=1（x<2）；若x的值为2，那么该正方形的面积为x2=4（x=2）；若该正方形的面积为x2=2，那么x=，这个到底是多长呢？大家分析一下，是大于2还是小于2？

生1：我认为应介于1，2之间.

师：介于1，2之间的数有很多，到底是哪个数呢？

生2：不对，我刚刚计算了，1.5的平方为2.25，该值显然大于2.

生3：1.42=1.96，小于2.

师：由此能说明什么？

生4：可见x是大于1.4的.

师：非常好！根据以上方法，我们可利用“二分法”无限计算，所获得的值会越来越接近. 如图2所示，这些数没有规律可循，不是无限循环小数，因此无法用分数表示，由此我们将此类数称为什么数？在这里表示什么？

生5：这类数就是无理数，在这里表示面积为2的正方形的边长.

师：非常好，这就是所蕴含的几何意义. 你们知道根号的由来吗？

（学生摇头，并充满渴望地望着老师）

师：在拉丁语中，根为radix；在英语中，根为root，这两者的首字母都是“r”，16世纪的斯蒂文和路多尔夫两人将“r”变形成了根号. 到17世纪，法国的笛卡尔在原來的基础上，将根号进行了完善，形成了今天我们所熟悉的“”. 现在请大家观看无理数历史发展的视频. （播放微视频）

设计意图  ①利用“二分法”估算的大小，其目的在于让学生深刻体会无理数不是无限循环小数，无法用分数来表示，从本源上将有理数和无理数进行了区分. ②引用正方形面积来理解，是为了让学生感知算术平方根的几何意义，由此渗透了重要的数形结合思想，并让学生体会并非所有带“”的数都是无理数. ③介绍根号的形成史，是为了让学生体会生活与数学的关系，数学概念是由生活实际抽象而来的，最后又反过来为更好地生活服务. 微视频的播放，能有效地激发学生对概念学习的兴趣.

此教学过程，教师将教材知识进行了重新整合，通过一定的教学手段，凸显了有理数与无理数的区别，深化了学生对无理数概念的认识. 这种教学设计不仅让学生感知了概念的产生与发展过程，对无理数的本源产生了理解，还让学生深刻体会了知识的衍生、发展，以及与生活的联系.

教育的本质是“教书育人”，知识的重要性，不言而喻，而“育人”的理念，可渗透到课堂的每个角落. 微视频的播放，激趣的同时，还让学生感知数学概念从无到有，逐渐完善的过程，知道我们所熟知的知识并非是天上掉下来的，而是经历了一个艰辛的探究与发展历程，体会在追求真理的学习道路上，只有保持坚持不懈、孜孜不倦、科学严谨的态度，不断地克服困难，才能实现质的飞跃.

李邦河院士提出：概念是数学的根本，数学学习玩的是概念，而非技巧［3］. 纵观近些年的中考试题，很多新颖的命题都源自概念，又高于概念. 因此，教师应从思想上重视概念教学，深入挖掘与探究概念的内涵与外延，这对发展学生的数学核心素养具有深远的影响.

参考文献：

［1］曹才翰，章建跃.数学教育心理学［M］北京：北京师范大学出版社，2014.

［2］李兴贵，王富英.数学概念学习的基本过程［J］. 数学通报，2014，53 （02）：5-8.

［3］李邦河. 数的概念的发展［J］. 数学通报，2009，48（08）：1-3，9.